直方图线性拉伸优化技巧

上面讲到直方图的形状可以反映出图像的一些质量特征。当一幅图像的对比度不够，或者图像偏暗、偏亮时，我们可以通过有目的地改变直方图形态来改善图像的对比度，从而提高图像质量。

在对图像进行对比度改善时，需要改变图像像元的原有亮度值，在这个运算过程中需要一个变换函数来进行有规律的改变。如果变换函数是线性的，或者分段线性的，那么就称为图像的线性拉伸；如果使用的函数是指数形式或者其他非线性函数，那么就称为图像的非线性拉伸。而线性变换是数字图像增强处理中最简单、最常用的方法。

以图4-1为例，其亮度值为1～20，根据其直方图，可以感觉该图像偏暗，现在对该图像进行线性拉伸（拉伸2倍），此时新的图像的亮度值是原图像亮度的两倍。所用的线性拉伸函数即为

Xnew＝2Xold

产生的新图像与相应的直方图如图4-4所示。比较数字图像，每一个像元上的亮度值都增加了一倍，此时的图形比原来的图像要亮一倍。同时比较直方图，此时直方图的亮度范围增加了一倍，在x轴上由过去的0～20的亮度值范围变为现在的亮度值0～40的亮度值范围；像素之间的对比度也得到增加，以第一像素与第二像素为例，由过去的亮度值4，2分别变为新亮度的亮度值8，4。这样像素之间的亮度差值由2变为4，因此对比度增强。总之，通过上述办法，改变后的图像有两点变化：一是图像整体亮度增加了一倍，二是像素之间的差异（对比度）有明显的改变。这种差异对于目视解译有很大好处。

图4-4　数字图像的线性拉伸，亮度增加2倍

线性拉伸函数一般使用Xnew＝aXold+b ，其中a、b取值由用户自行设定和调整，直到图像显示效果达到最佳为止。

有时为了更好地调节图像的对比度，需要在一些亮度段增大拉伸幅度，而在另外一些亮度段减小拉伸幅度。这种变换称为分段线性拉伸。很显然这样的线性拉伸使用分段线性函数，性质与线性拉伸相同。

当亮度变换函数使用非线性函数时，此时即为图像的非线性拉伸。非线性变换的函数很多，常用的有指数变换和对数变换。

指数拉伸的变换函数如图4-5所示。利用指数函数的性质，其函数的变化率在逐渐增大。这样对图像进行指数拉伸后，图像中亮度值较高的部分在亮度增加同时，扩大了像素之间的亮度间隔，突出了差异，而对于亮度值较低的部分，在亮度增加的同时，像素之间的亮度间隔变化不大，对比度保留了原有的差异。其数学表达式为(www.xing528.com)

Xnew＝aeXold+b

上式中，a、b为可调参数，通过改变它们可以改变指数函数曲线的形态，从而实现不同的拉伸比例。

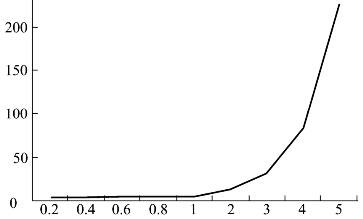
图4-5　指数拉伸

对数变换的变换函数如图4-6所示。与指数变换相反，其函数的变化率在逐渐减小，并且趋于0。因此它的意义与指数变换相反，在图像比较亮的地方，没有增加像素之间的对比度，而在图形暗的地方增加了像素之间的对比度。其数学表达式为：

Xnew＝aln（Xold+1）+b

注意在上式中，使用Xold+1来代替Xold，是为了防止在对数运算中，真数出现等于0的情形。其他参数含义同上，可以进行改变。

图4-6　对数变换

在图像处理中，还有一种变换，称为图像的反色变换。它是将原图灰度值进行翻转。即将原图像中黑的变成白的，将白的变成黑的。犹如在过去化学成像中的底片一样。在过去胶片时代，人的头发在底板中呈现白色，而只有通过洗相后，才会在黑白照片中呈现黑色。图像的反色变换可以看成是线性拉伸的特殊情况。反色变换函数可用如下函数表达式进行：

Xnew＝255-Xold