杆系拉压极限分析

一、是非题

1.由于轴向拉压杆横截面上的应力是均匀分布的,因此拉压杆系初始屈服时的屈服载荷与完全屈服时的塑性极限载荷是相同的。( )

2.材料处于塑性变形阶段时,其总应变包含弹性应变和塑性应变两部分。( )

二、选择题

1.在弹塑性计算中,理想弹塑性材料的应力-应变图应为图13.1( )。

(A)(a)　(B)(b)　(C)(c)　(D)(d)

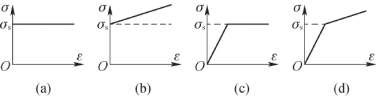
图13.1

2.关于解除外力后,消失的变形和残余的变形的定义,以下结论中正确的是( )。

(A)分别称为弹性变形、塑性变形　(B)通称为塑性变形

(C)分别称为塑性变形、弹性变形　(D)通称为弹性变形

三、填空题

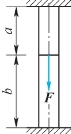
图13.2

2.简单桁架如图13.3所示,两杆的横截面积均为A,材料为理想弹塑性,屈服应力为σs,则桁架的极限载荷为________。

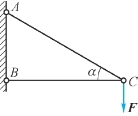
图13.3

四、计算题

1.弹性模量E=200 GPa的试件,其应力-应变曲线如图13.4所示,点A为屈服极限σs=240 MPa。当拉伸至点B时,在试样的标距中测得纵向线应变为3×10-3,试求从点B卸载到应力为140 MPa时,标距内的纵向线应变ε。

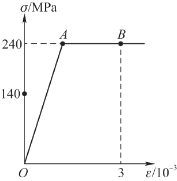
图13.4

2.图示13.5(a)所结构由两根横截面相同的圆管铰接而成,圆管的横截面积A=55 mm2,惯性矩Iz=4 200 mm4,材料的σ-ε曲线如图13.5(b)所示,弹性模量E=210 GPa,试求:

(1)随着载荷F的增大,哪根圆管先失效;(www.xing528.com)

(2)结构能承受的极限载荷F。

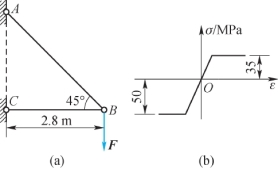
图13.5

3.超静定杆系受力如图13.6所示,各杆的横截面积均为A,材料为理想弹塑性,屈服应力为σs。试求杆系的屈服载荷Fs和塑性极限载荷Fp。

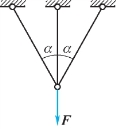
图13.6

【参考答案】

一、是非题

1.非 2.是

二、选择题

1.C 2.A

三、填空题

四、计算题

1.点B应变包括两部分:εe(弹性)和εP(塑性)

取最小值,则F=1.11 kN。

3.受力分析如图13.7所示。

杆1先屈服,屈服载荷Fs=(1+2 cos3α)σsA。

杆2和3屈服时,塑性极限载荷Fp=(1+2cosα)σsA。

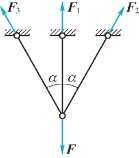
图13.7