水平冲击的效应及应对措施

设一水平放置等直杆如图12.10(a)所示,杆长为l,横截面积为A,材料的弹性模量为E。一重量为Q的冲击重物以速度v沿水平方向冲击杆的自由端。现在分析等直杆内的最大冲击变形和冲击应力。

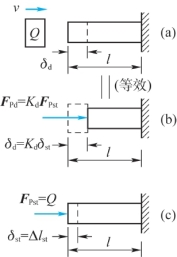
图12.10　水平冲击

式中:δst是指将重物的重量Q以静载荷的方式沿冲击方向作用于冲击点,所引起的冲击点沿冲击方向的静位移,如图12.10(c)所示。

可求得本例如图12.10所示等直杆水平冲击时的动荷因数为

综上所述,可知杆所受到的最大冲击动载荷

最大冲击动应力

冲击点最大动位移

冲击动荷因数Kd的表达式(12.7)、式(12.8)和式(12.10)均是根据构件受不同类型冲击时发生轴向变形的情况导出的。而对于受冲击作用而发生弯曲变形的构件,如图12.11(a)(b)、(c)也适用,冲击点静位移δst的定义也相同,只是计算公式有差异。对于受冲击作用而发生弯曲变形或扭转变形的较复杂的情形,如图12.11(d)所示,则可根据构件受冲击时发生变形的情况由能量守恒定律分别导出不同的Kd表达式。有时也可先求得动荷因数Kd后,再用能量守恒定律求出冲击应力和冲击变形。(www.xing528.com)

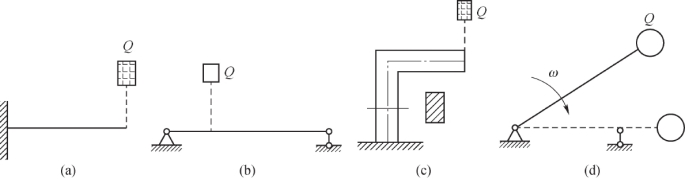
图12.11　构件受到其他较复杂的冲击情形

【例12.5】一下端固定、长度为l、直径为d的铅直实心圆截面杆AB,在点C处被一重物Q沿水平方向冲击,如图12.12(a)所示。已知点C到杆下端的距离为a,重物Q的重量为Q,Q在与杆接触时的速度为v。试求杆在危险点处的冲击动应力。

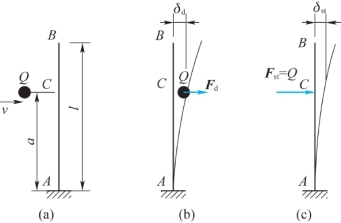
图12.12　例12.5图

【解】(1)计算动荷因数。

在水平冲击情况下的动荷因数Kd可直接引用式(12.10),得

上式中δst是指将重物的重量Q以静载荷的方式沿冲击(水平)方向作用于冲击点,所引起的冲击点沿冲击方向(水平)的静位移,如图12.12(c)图所示,即

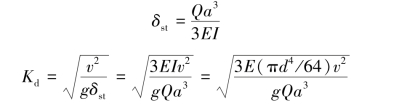
(2)计算冲击动应力。

现将重物的重量Q以静载荷的方式沿冲击(水平)方向作用于杆上的点C,使得杆的固定端横截面最外边缘(即危险点)处产生的静应力为

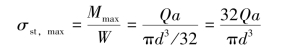
于是,杆在上述危险点处的冲击应力σd,max可直接引用式(12.9),得

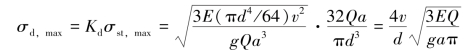
本题也可利用图12.12(b),先由能量守恒定律导出Kd表达式,再进行后续计算。