构件匀角速度转动优化方案

在某些工程问题中,构件承受动载荷,但不存在相应的静载荷,也就无法用式(12.4)计算其动荷因数,例如匀角速转动的构件。

当构件做匀角速转动时,构件上各质点只有向心加速度,向心加速度的值rω2,r是质点到转轴的距离,ω是构件的角速度。按照达朗贝尔原理,将离心惯性力加到构件的每个质点上,则惯性力系与构件上的外力在形式上组成一个平衡力系。将动力问题简化为静力平衡问题进行计算。

如图12.4(a)所示,薄壁圆环以匀角速度ω绕圆心旋转,圆环厚为t,直径为D,宽为b,径向截面面积为A=tb,圆环密度为ρ,重度为ρg。设在单位宽度的微段弧长ds上的离心惯性力dp,则

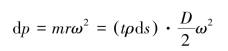
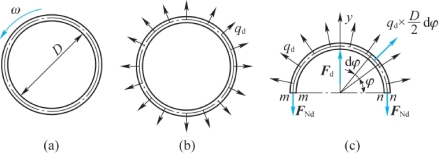
图12.4　薄壁圆环以匀角速度旋转

(a)匀角速转动圆环;(b)圆环的惯性力系;(c)半圆环受力图

旋转薄壁圆环的离心惯性力构成径向的均布载荷,其惯性载荷集度为

相应的静载荷集度为

动载荷集度为

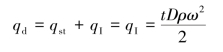
而圆环承受的动载荷如图12.4(b)所示,这与薄壁容器受内压时的载荷图类似。

由于圆环几何外形、物性及受力的极对称性,用任一直径平面截取半圆环受力如图12.4(c)所示,半环上的惯性力沿y轴方向的合力为

其作用线与y轴重合。

由对称关系可知,半圆环两侧径向截面m—m(或n—n)上的轴力FNd相等,其值可由平衡方程∑Fy=0求得,为

由于环壁很薄,可认为在圆环径向截面m—m(或n—n)上各点处的正应力相等。于是,旋转薄壁圆环的径向截面上的正应力σd为

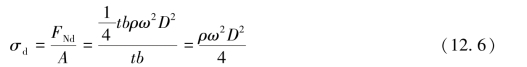
由式(12.6)知,旋转薄壁圆环的周向应力与圆环的壁厚、环宽无关。欲提高构件的安全性,加宽加厚构件的做法是有害无益的,应采用轻质材料或改圆环为圆盘型构件。由于匀速转动的动载荷不存在对应的静载荷、静应力,因此,此时不存在动荷因数。

对于其他形式的旋转构件而言,也有与式(12.6)类似的应力表达式。旋转构件的应力跟角速度的平方成正比,高速旋转的构件内或半径较大的构件内存在相当大的拉应力,故为了保证构件安全工作,必须严格限制构件的转速。

对于旋转薄壁圆环,其强度条件为(www.xing528.com)

则旋转薄壁圆环的限速为

在离心惯性力(惯性动载荷)qd作用下,圆环的周长l和平均直径D都将增加。以ΔD表示直径的增量,εt表示周向应变,则有

由此得到ΔD=εtD。

在线弹性范围内,由胡克定律得

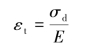
代入上式,得平均直径的增量(即旋转圆环的变形)为

可见,圆环直径的改变量与ω2成正比。当飞轮的轮缘与轮心采用过盈配合时,若转速过大,则有可能发生轮缘与轮心松脱现象。

【例12.2】如图12.5所示,传动轴AB的A端安装有飞轮,转动惯量J=10.8 N·m·s2,飞轮的转速n=3 000 r/min。B端装有刹车离合器,轴AB的许用应力[σ]=80 MPa,若要求飞轮在t=25 s内停止转动,试设计轴AB的直径d。

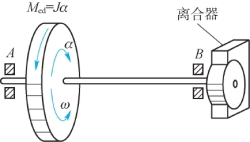
图12.5　例12.2图

【解】由理论力学知:惯性力系对转轴的主矩,即惯性力偶矩Med,其大小等于构件的转动惯量J与角加速度α的乘积,其转向与角加速度方向相反,如图12.5所示,即

假定轮A是匀减速停下,那么

轴AB受到飞轮A给予的惯性力偶矩Med和刹车离合器给予的制动力偶矩作用,产生扭转变形,扭矩MT=Med。因此轴内最大切应力为

若按第三强度理论设计,应有

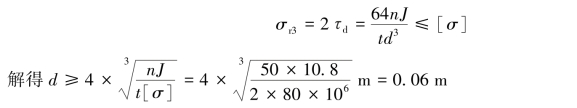
故轴AB的直径应不小于60 mm。