构件匀加速直线平动的原理及应用

现以匀加速起吊一根杆件为例,说明构件作匀加速直线运动时的动应力计算方法。设杆件长为l,重量为W,杆件密度为ρ,重度为ρg,横截面积为A,在吊索牵引下以加速度a上升,如图12.2(a)所示,现分析此吊杆的内力、应力和变形。

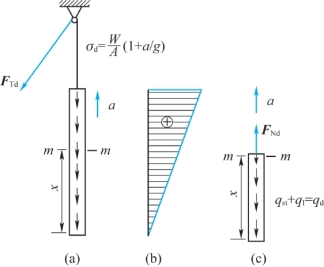
图12.2　匀加速起吊一根杆件

(a);(b)轴力图;(c)x段受力图

作用在杆上的自重(静载荷)沿杆轴线均匀分布,其静载荷集度为qst=Aρg;惯性力也沿杆轴线均匀分布,其惯性载荷集度为qI=Aρa,惯性载荷方向与加速度a相反(向下)。可见,其动载荷集度为

沿任一横截面m—m将杆截开,并取长为x的下段为研究对象,设m—m截面的动轴力为FNd(x),如图12.2(c)所示。由动静法,列出平衡方程

由此可得m—m截面的动轴力为

m—m横截面上的动应力为

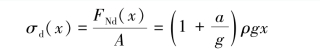
因W=Aρgl,故上面两式可改写成

所以

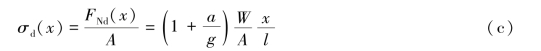
动应力沿杆长的分布规律如图12.2(b)所示,由式(a)可得吊索动拉力FTd(杆端所受牵引力)

当加速度a=0时,杆件静止或做匀速直线平动,则可得吊索的静拉力FTst、杆件m—m截面上的静轴力FNst、静应力σst分别为

代入以上各式,归纳得出

这里的Kd称为构件匀加速直线平动时的动荷因数或称动荷系数(dynamic factor)。

由此可见,构件的动载荷、动内力和动应力分别等于动荷因数乘以构件相应的静载荷、静内力和静应力。而在线弹性范围内,应变与应力成正比,变形与载荷成正比,故也可将杆的动应变εd和动变形Δld分别表示为静应变εst和静变形Δlst与动荷因数的乘积,即

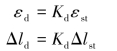
综上所述,构件在动载荷作用下的各种动内效应量(如动内力、动应力、动应变、动位移等)等于动荷因数乘以构件在静载荷作用下相应的各种静内效应量(如静内力、静应力、静应变、静位移等),即(www.xing528.com)

动荷因数Kd可理解为动内效应量是相应的静内效应量的倍数。且在同一工况下,构件或系统的动荷因数是唯一的,即

对于匀加速直线平动下构件的强度条件为

动载荷下构件的强度计算的关键是求动荷因数Kd。式(12.5)中的[σ]为材料在静载荷下的许用应力值。

必须指出,上面的结论也适用于等直梁在动载荷下的平面弯曲的情况,还适用于冲击载荷的情况。当然式(12.3)、式(12.4)中的内效应量就要做相应的调整和扩充。

【例12.1】如图12.3所示,一根长度l=12 m的14号工字钢,由两根钢缆吊起,并以匀加速度a=15 m/s2上升,如图12.3(a)所示。已知钢缆的横截面积A=72 mm2,工字钢的许用应力[σ]=160 MPa,试计算钢缆的动应力,并校核工字钢梁的强度。

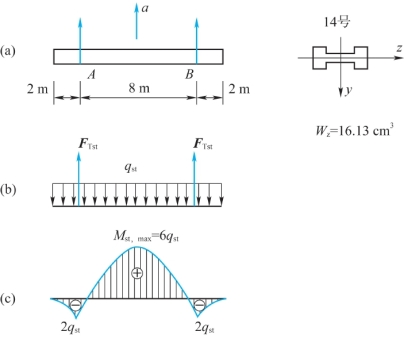
图12.3　例12.1图

【解】由型钢表查得:工字钢每米长度的重量qst以及抗弯截面系数Wz

计算动荷因数

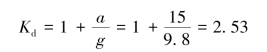
工字钢梁在自重(静载荷)作用下的受力图如图12.3(b)所示,由钢梁的平衡条件∑Fy=0,解得钢缆所受的静拉力FTst以及静应力σst

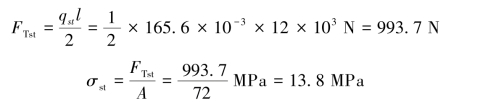
故钢缆内的动应力为

绘出工字钢梁在静载荷qst作用下的弯矩图,如图12.3(c)所示,在跨中截面有最大弯矩

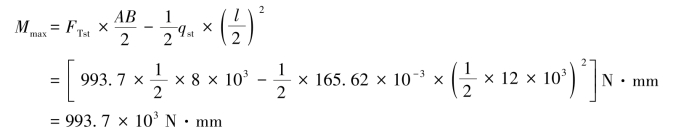
在跨中截面上下边缘有最大应力

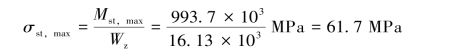
工字钢梁内最大动应力

故工字钢梁是安全的。