超静定结构的能量法求解

一、是非题

1.求解超静定结构时,若取不同的静定基,则补充方程不同,但解答结果相同。( )

2.等截面直梁及其受力状态如图11.38所示。若利用其反对称性从截面C截开选取静定基,则该问题可简化为一次超静定问题,其中多余约束力为FSC,变形协调条件为wC=0。( )

图11.38

3.结构的超静定次数等于支座反力数目与独立平衡方程数目的差数。( )

4.超静定系统与其相当系统相比,二者的内力和变形都相同。( )

5.超静定结构的相当系统和补充方程不是唯一的,但其计算结果都是唯一的。( )

二、填空题

1.图11.39所示平面结构为________次超静定。

图11.39

2.判断图11.40所示各平面结构的超静定次数(面内受力)。

图11.40

3.有一两端固定的梁AB如图11.41所示,在点C受一集中力F的作用。梁AB为________次超静定。

图11.41

4.求解图11.42示梁B端的支反力FBy时,若解除B端约束,其变形协调条件为________;则FBy=________。

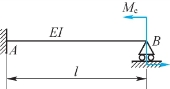
图11.42

5.如图11.43所示,已知梁AB的弯曲刚度EI和杆BC的拉压刚度EA。欲求杆BC的内力FN,则其变形协调条件为________。

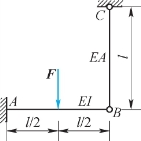
图11.43

三、计算题

1.图11.44所示AB梁的A端为导向支承,B端为固定支承,AB梁的弯曲刚度为EI,试用能量法求支承A处的位移。

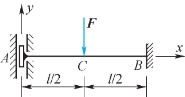
图11.44

2.用能量法求图11.45所示等截面梁中央横截面C的弯矩MC。

图11.45

3.具有中间铰的两端固定梁如图11.46所示,已知q、EI、l,用能量法求梁的支反力,并绘出梁的剪力图和弯矩图。(www.xing528.com)

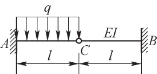
图11.46

4.结构及其受力如图11.47所示。已知EA、EI,且I=Aa2,用卡氏第二定理求杆1和杆2的内力。

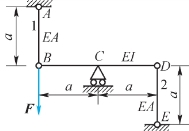
图11.47

5.已知图11.48所示结构拉杆BC的拉压刚度EA、梁AB的弯曲刚度为EI,试求拉杆BC的轴力。

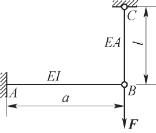
图11.48

【参考答案】

一、是非题

1.是 2.是 3.非 4.是 5.是

二、填空题

1.1

2.0;2;1;0

3.2

三、计算题

1.

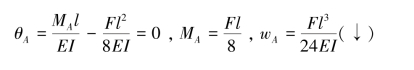
2.

3.

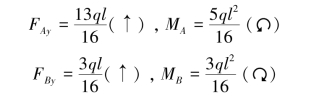
梁的剪力图和弯矩图如图11.49所示。

图11.49

4.

5.受力分析如图11.50所示。

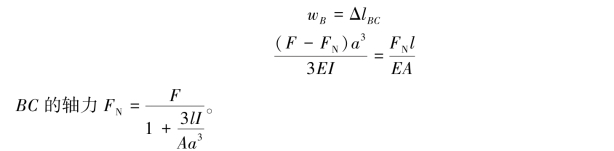
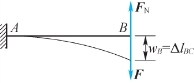
图11.50