【摘要】：卡氏第二定理也可通过前面章节中的例题来简单地验证。几种杆系结构的卡氏第二定理具体表达式如下。用卡氏定理求结构某处的位移时,该处需要有与所求位移相应的载荷,如果计算某处位移,而该处没有与此位移相应的载荷,则可采用附加力法,下例说明。图11.6正三角形桁架根据卡氏定理,桁架在任一外力P作用点的相应位移为列表计算如表11.1所示。
一、选择题
1.一刚架承载如图11.10所示,其弹性应变能Vε,则由卡氏定理δ=
求得的位移是( )。
(A)截面A水平位移和铅垂位移的代数和
(B)截面A水平位移和铅垂位移的矢量和
(C)截面A沿合力方向(45°)的位移
(D)截面A的总位移
图11.10
2.根据卡氏第二定理求图11.11所示梁截面B的挠度时,下列答案中正确的是( )。
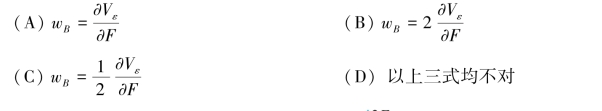
图11.11
3.如图11.12所示简支梁,利用卡氏第二定理表示C、D截面挠度,下列各式中正确的是( )。
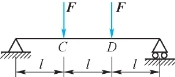
图11.12
二、填空题
1.如图11.13所示,外伸梁的弯曲刚度EI为常数,在自由端作用集中力F,则截面B处的转角为θB=________,截面C处的挠度wC=________。
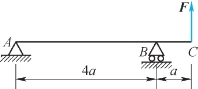
图11.13
2.图11.14所示刚架采用卡氏第二定理求位移,则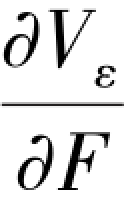
代表________。
图11.14(www.xing528.com)
三、计算题
1.悬臂梁如图11.15所示,已知:F、a、M=Fa,弯曲刚度为EI,试用卡氏第二定理求截面C的转角和挠度。
图11.15
2.简支梁受载如图11.16所示,已知:F、a、M=Fa,梁的弯曲刚度为EI,试用卡氏第二定理求中间截面C的挠度。
图11.16
3.外伸梁受载如图11.17所示,已知:F、l、a,梁的弯曲刚度为EI,试用卡氏第二定理求截面A的转角和截面D的挠度。
图11.17
4.平面刚架受载如图11.18所示,已知:F、a,弯曲刚度为EI,试用卡氏第二定理求截面A的转角。
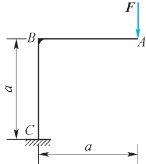
图11.18
【参考答案】
一、选择题
1.A 2.C 3.B
二、填空题
2.点A水平位移和铅垂位移的代数和
三、计算题
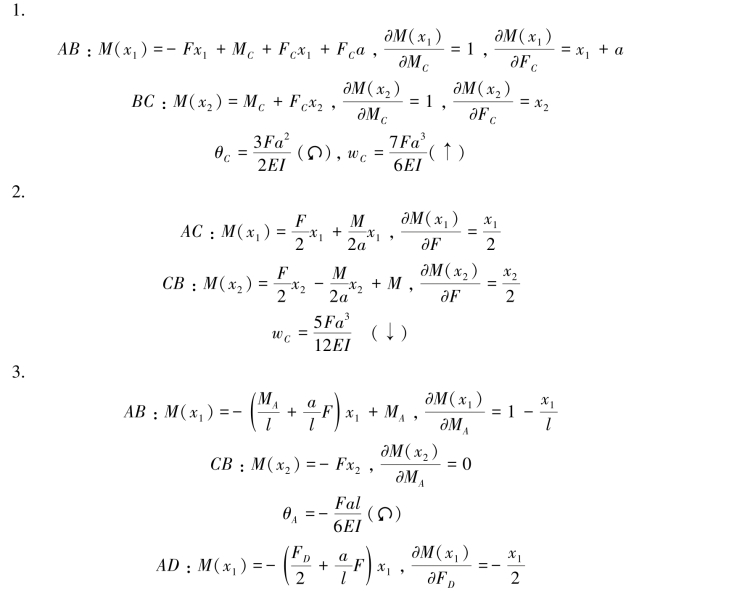
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
