弯曲和扭转的组合变形现象

弯曲与扭转组合变形是机械工程中常见的情况。以图9.6所示一端固定的曲拐为例,说明弯曲与扭转组合变形的强度计算方法。设拐轴AB段为等圆杆,直径为d,A端为固定端约束。现分析在力P作用下轴AB的受力情况。

二维码

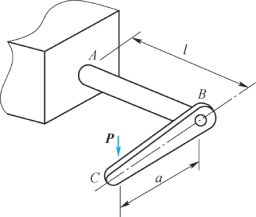
图9.6　曲拐在P作用下的变形

将力P向轴AB截面B的形心简化,得到一横向力P和作用在轴端平面内的力偶矩M=Pa,轴AB的受力简图如图9.7(a)所示。横向力P使轴AB发生弯曲变形,力偶矩M使轴AB发生扭转变形。P和M共同作用下,轴AB发生弯、扭组合变形。

分别绘出轴AB的弯矩图和扭矩图,如图9.7(b)、图9.7(c)所示。一般情况下,横向力引起的剪力影响较小,可忽略不计。由图9.7可知,各横截面的扭矩相同,均为T=Pa,各截面上的弯矩则不同。显然固定端截面的弯矩最大,其值为Mz=Pl。所以轴AB的危险截面为固定端截面。

危险截面上与弯矩和扭矩对应的正应力和切应力分布情况示于图9.7(d),与弯矩所对应的正应力σ,沿截面高度按线性规律变化,该截面沿铅垂直径的两端点a和b的应力最大;与扭矩T所对应的切应力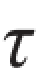,沿半径按线性规律变化,该截面周边各点的切应力为最大,分别为

综合考虑正应力和切应力可知,危险截面上离中性轴最远的上、下两点a、b是危险点,其应力状态如图9.7(e)所示,该两点均为平面应力状态,利用式(8.4)可求得这两点的主应力均为

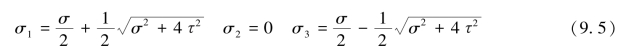
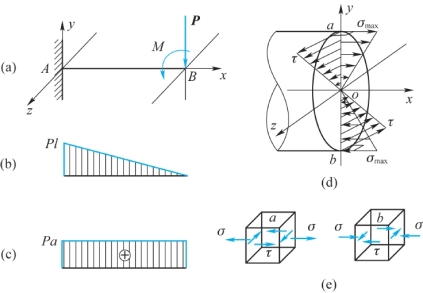
图9.7　杆AB的受力和截面A的应力

若轴由抗拉和抗压强度相等的塑性材料制成,则可选用第三或第四强度理论,若按第三强度理论,由σr3=σ1-σ3得其强度条件为

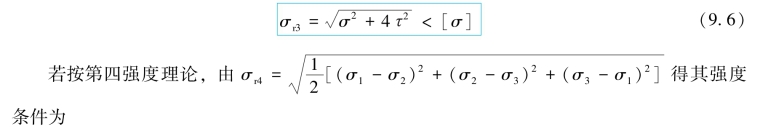
将式(9.4)代入式(9.7)得圆轴弯曲与扭转组合变形,按第四强度理论的强度条件为

由式(9.8)和式(9.9)可知,对于弯曲和扭转组合变形,在求得危险截面的弯矩(或合成弯矩)M和扭矩T后,就可直接利用式(9.8)或式(9.9)进行强度计算。式(9.8)和式(9.9)同样也适用空心圆轴,仅需将式中的W改为空心截面的抗弯截面系数。

值得注意的是:式(9.6)和式(9.7)适用于如图9.7(e)所示的平面应力状态,而发生这一应力状态的组合变形可以是弯曲与扭转的组合变形,也可以是拉伸与扭转的组合变形,还可以是拉伸、弯曲和扭转的组合变形;而式(9.8)和式(9.9)只能用于圆轴的弯曲与扭转的组合变形。

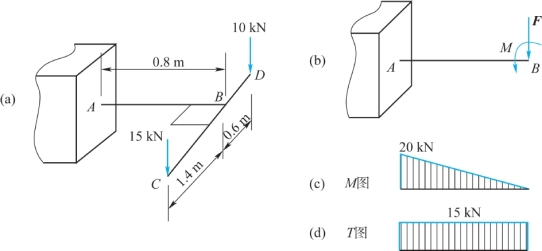
【例9.4】空心圆杆AB和CD焊接成整体结构,受力如图9.8(a)所示。杆AB的外径D=140 mm,内、外径之比α=d/D=0.8,材料的许用应力[σ]=160 MPa。试用第三强度理论校核轴AB的强度。

(www.xing528.com)

图9.8　例9.4图

【解】将两外力分别向杆AB的截面B形心简化,如图9.8(b)所示,得

故,杆AB发生扭转和平面弯曲的组合变形。

分别作AB段弯矩图和扭矩图,如图9.8(c)、图9.8(d)所示,由内力图可知固定端截面A为危险截面。危险截面上的扭矩和弯矩分别为

若按第三强度理论进行校核,则由式(9.7)可得

所以,轴AB满足第三强度理论的强度要求,是安全的。

【例9.5】如图9.9所示一钢制实心圆轴,齿轮C上作用有铅垂切向力5 kN,径向力1.82 kN;齿轮D上作用有水平切向力10 kN,径向力3.64 kN。齿轮C的节圆直径d1=400 mm,齿轮D的节圆直径d2=200 mm。设许用应力[σ]=100 MPa。试按第四强度理论确定轴的直径。

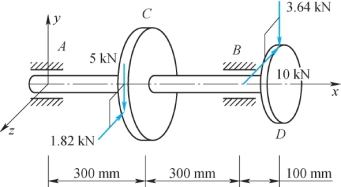
图9.9　例9.5图

【解】为了分析该轴的基本变形,将每个齿轮上的外力向该轴的截面形心简化,其结果如图9.10(a)所示。由图可知:沿z方向的力使圆轴在xz纵对称面内产生弯曲,沿y方向的力使轴在xy纵对称面内产生弯曲,力偶1 kN·m使轴产生扭转。

根据图9.10(a)所示受力简图,绘制轴的内力图如图9.10(b)、图9.10(c)、9.10(d)所示,其中

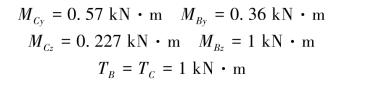
由此可知,该圆杆分别在xy和xz平面内分别发生平面弯曲,同时发生扭转变形,由于通过圆轴轴线的任一平面都是纵向对称平面,故轴在xz和xy两平面内弯曲的合成结果仍为平面弯曲,从而可用合成弯矩来计算相应截面弯曲正应力。则截面B、C的合成弯矩分别为

因MB＞MC,TB=TC,可判定截面B是危险截面。

对于危险截面B,由第四强度理论进行计算,即由式(9.9)得

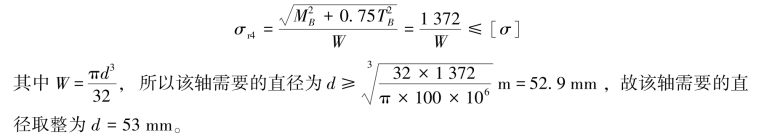
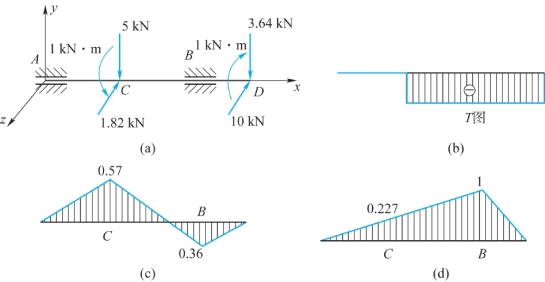
图9.10　实心圆轴的内力分析