切应力极值及其所在平面分析

特别注意:不能用式(8.6)来求解空间应力状态下或特殊空间应力状态下的最大和最小切应力,而应当用下一节中的公式(8.7)来求解。

比较式(8.3)与式(8.5)可得

故有

图8.4　例8.2图

式(d)表明最大和最小切应力所在平面与主平面的夹角为45°。

【例8.2】直径为d=100 mm的等直圆杆,受轴向力F=500 kN及外力偶M=7 kN·m作用,如图8.4(a)所示。试求:(1)杆表面点C处由横截面、径向截面和周向截面取出的单元体上各面上的应力,如图8.4(b)所示;(2)该点处与母线夹角为30°斜截面上的应力情况;(3)该点的主应力、主方向。

【解】(1)由轴向拉压和扭转的应力分析可得,点C处的应力情况为

(www.xing528.com)

按主应力记号规定σ1≥σ2≥σ3,得单元体的3个主应力分别为

由式(8.3),得

所以,α0=24.12°或-65.88°。请读者自行绘制主单元体。

【例8.3】试分析图8.5(a)所示受扭圆轴表面任一点的主应力,说明引起圆铸铁试样扭转破坏的主要原因。

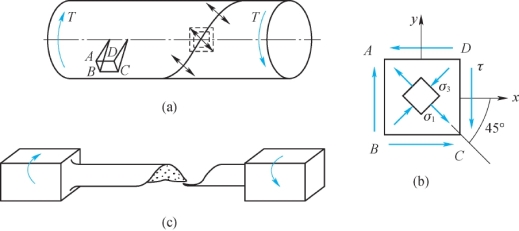
图8.5　例8.3图

【解】在受扭圆轴表面上任选一点A(见图8.5(a)),围绕该点用横截面和纵截面截取一个单元体,如图8.5(b)所示。由前面章节可知,这一单元体的侧面上只有切应力作用,即圆轴扭转时,其上任一点的应力状态都是纯剪切应力状态,为

将上述应力代入式(8.4)和式(8.3),得

以上结果表明:由x轴,按顺时针方向转45°可确定主应力σ1的主平面,按顺时针方向转135°可确定主应力σ3的主平面,如图8.5(c)所示。铸铁圆轴扭转试验时,正是沿着最大拉应力作用面(即-45°螺旋面)断开的。因此,可以认为铸铁的这种脆性破坏是由最大拉应力引起的。