任意斜截面应力的计算方法

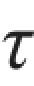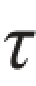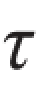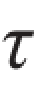在图8.3(a)所示的单元体的各侧面上,设应力分量σx,σy,xy和yx均已知,图8.3(b)为单元体的正投影。各应力分量的下标具有如下含义:σx和σy,分别表示x平面和y平面上的正应力;xy第一个下标x表示切应力作用面的法线方向,第二个下标y表示切应力平行于y轴;yx与之类似。根据切应力互等定理,xy=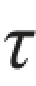yx。应力的正负号规定为:正应力以拉应力为正、压应力为负;切应力对单元体内任一点的矩为顺时针转向时为正,反之为负。按照这一规定,图8.3(a)和图8.3(b)中的σx,σy,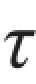xy均为正,而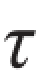yx为负。

欲求与z轴平行的任意斜截面ef(见图8.3(b))上的应力,设斜截面ef的外法线n与x轴成α角,称该斜截面为α斜截面,其上的正应力和切应力分别用σα及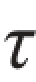α表示。为便于计算,将α角正负号规定为:从x轴转至α斜截面的外法线,逆时针转为正,反之为负。

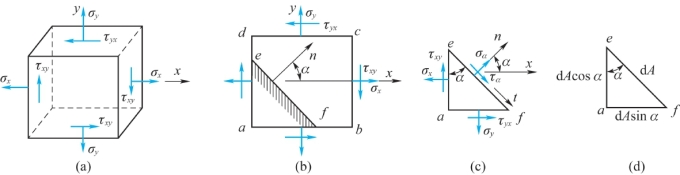
图8.3　任意斜截面上应力

为了求得α斜截面上的正应力和切应力,利用截面法,沿斜截面ef将单元体分成两部分,并研究下半部分aef的平衡,如图8.3(c)所示。设截面ef的面积为dA,则截面ae与af的面积分别为dAcosα与dAsinα,如图8.3(d)所示。把作用于aef部分上的力投影于ef面的外法线n和切线t的方向,可得其平衡方程为(www.xing528.com)

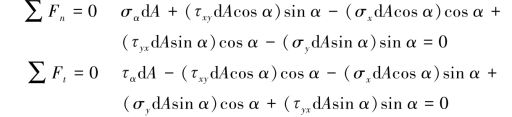
根据切应力互等定理,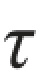xy与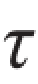yx在数值上相等,以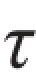xy代替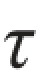yx,化简上述两个平衡方程,得

由式(8.1)和式(8.2)可知,当σx,σy,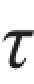xy已知时,可以求出α为任意值时斜截面上的应力。这种方法称为解析法。