【摘要】：设x轴沿梁轴,向右为正,w轴向上为正。列出弯矩方程,即利用式计算变形能,即图7.17例7.11图计算外力功,即根据功能原理U=W得即与表7.1中的结果相同。利用功能原理计算图7.18中简支梁截面C的挠度wC。AC段图7.18例7.12图CB段利用式计算变形能,即计算外力功,即根据功能原理U=W得,即直接利用功能原理通常只能求集中载荷作用处与载荷对应的位移,即求集中力作用点处的线位移或者力偶矩作用点处的转角位移。
利用功能原理U=W求外力作用点沿着外力方向的位移时,不管是集中力作用点的线位移δ还是力偶矩作用点的转角位移θ,由于都是缓慢加载,因此外力从0开始逐渐增加到最终值,则相应的位移也是从0开始逐渐增加。外力在相应位移上所做的功为
下面利用功能原理来求解弯曲变形。
【例7.11】利用功能原理计算图7.17中悬臂梁B端的转角。
【解】设x轴沿梁轴,向右为正,w轴向上为正。
(1)列出弯矩方程,即
(2)利用式(7.13)计算变形能,即
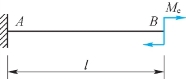
图7.17 例7.11图
(3)计算外力功,即
(4)根据功能原理U=W得
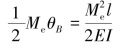
即
(www.xing528.com)
与表7.1中的结果相同(此处的正号表示计算的位移同载荷的方向一致,因为载荷做正功)。
【例7.12】利用功能原理计算图7.18中简支梁截面C的挠度wC。
【解】设x轴沿梁轴,向右为正,w轴向上为正。
(1)列出弯矩方程。
AC段
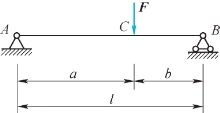
图7.18 例7.12图
CB段
(2)利用式(7.13)计算变形能,即
(3)计算外力功,即
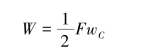
(4)根据功能原理U=W得,即
直接利用功能原理通常只能求集中载荷作用处与载荷对应的位移,即求集中力作用点处的线位移或者力偶矩作用点处的转角位移。而二次积分法虽说计算要麻烦一些,但是求出的是一般方程,即任意点处的线位移和转角位移。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
