同一个超静定梁,可以选取不同形式的静定梁为静定基,选取的静定基不同,多余约束不同,相应的变形协调条件和补充方程也随之发生变化,但解出的全部约束反力则是相同的。例如,图7.13(a)所示的超静定梁,也可选取如图7.13(c)所示的简支梁为静定基(方案2),此时是以固定端限制截面A的转动为多余约束,相应的多余约束反力为固定端的约束反力偶mA。因为超静定梁A端为固定端,故相应的变形协调条件为
![]()
求得的约束反力与前面解答完全相同,读者可自行演算,当然对于这种静定基也可以用积分法求解。
以上解超静定梁的方法,是通过比较静定基与原超静定梁在多余约束处的变形,从而建立补充方程解出多余约束反力的,这种方法称为变形比较法(属于力法)。
变形比较法求解超静定梁的方法和步骤归纳如下。
(1)确定超静定次数,用未知力的数目减去平衡方程的数目便得超静定次数。
(2)选取静定基,去掉多余约束并以相应的多余约束反力代替其作用。
(3)列出变形协调条件,根据静定基与原超静定梁在多余约束处的变形进行比较。
(4)建立补充方程并解出多余约束反力,分别计算静定基中各载荷及多余约束反力在多余约束处的变形,并代入变形协调条件中,即得补充方程,由此可解出多余约束反力。
多余约束反力确定后,作用在静定基上的所有载荷均为已知,由此即可按照分析静定梁的方法,继续进行有关计算,如计算内力、应力和位移等。
【例7.10】图7.15所示双跨梁ABC受均布载荷q作用,EI为常量。试作出此梁的剪力图和弯矩图(按机械类符号规定表示)。
【解】(1)选取静定基。
显然此梁具有一个多余约束,设中间支座B为多余约束,多余约束反力为FBy。得到图7.15(b)所示的简支梁为静定基。
(2)列出变形协调条件。
多余约束B处的挠度等于0,得变形协调条件为
![]()
B处的挠度是由集中力FBy和均布载荷q的作用共同引起的,因此有(https://www.xing528.com)
![]()
式中:wB,q和wB,FBy分别表示均布载荷q和多余约束反力FBy在B点引起的挠度。
查表7.1得

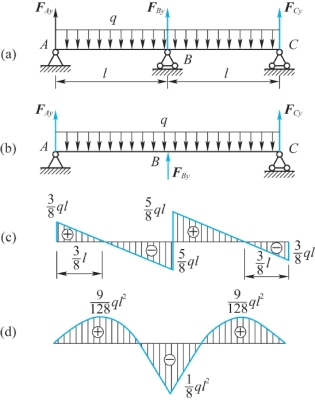
图7.15 例7.10图
(a)超静定梁;(b)静定基;(c)FS图;(d)M图
(3)建立补充方程。
将式(c)、式(d)代入式(b),得补充方程为
![]()
由此解得多余约束反力为
![]()
根据静定基的静力平衡条件,可求得其余两个支座反力为
![]()
支座的约束反力求出后,便可作出梁的剪力图和弯矩图,如图7.15(c)、(d)所示。
如果利用对称性,取一半结构来进行分析,因支座B处的转角为0,便可得到如图7.14所示的结构,从而简化计算。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




