叠加法求解梁的弯曲变形

一、是非题

1.只要梁内最大工作应力σmax≤材料比例极限σp,且梁变形为小变形,就可应用叠加法求梁的位移。( )

2.图7.17所示两梁的弯曲刚度EI相同,则两梁的跨中截面挠度不等,但转角相等,即:wCa≠wCb,但θCa=θCb。( )

图7.17

二、选择题

(A)1/2　(B)1/4　(C)1/6　(D)1/8

图7.18

2.两根材料相同、弯曲刚度相同的悬臂梁Ⅰ、Ⅱ如图7.19所示,则( )。

(A)Ⅰ梁和Ⅱ梁的最大挠度相同　(B)Ⅱ梁的最大挠度是Ⅰ梁的2倍

(C)Ⅱ梁的最大挠度是Ⅰ梁的4倍　(D)Ⅱ梁的最大挠度是Ⅰ梁的1/2倍

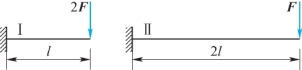
图7.19

3.图7.20所示等截面梁中点D的挠度为( )。

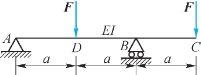
图7.20

三、填空题

1.图7.21所示等截面简支梁C处的挠度wC为________。

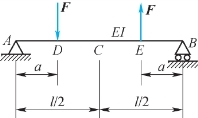
图7.21

2.图7.22所示等截面梁点C的挠度wC=________和点D的挠度wD=________。

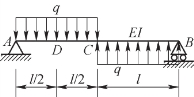
图7.22

四、计算题

1.悬臂梁的受力如图7.23所示,梁的弯曲刚度为EI。(www.xing528.com)

(1)定性绘出该梁的挠曲线;

(2)求点D的挠度wD值。

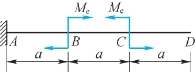
图7.23

2.试用叠加法求图7.24所示梁截面B的转角θB和挠度wB。

图7.24

3.图7.25所示梁B处为弹簧支座,弹簧刚度为k。试求A端的挠度wA。

图7.25

【参考答案】

一、是非题

1.是 2.是

二、选择题

1.D 2.C 3.D

三、填空题

1.0

四、计算题

1.(1)挠曲线如图7.26所示。

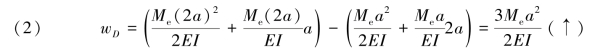
图7.26

2.

3.