用积分法求解梁的弯曲变形方法

一、是非题

1.只要满足线弹性条件,就可应用挠曲线近似微分方程,并通过积分法求梁的位移。( )

2.若两梁弯曲刚度相同,且弯矩方程M(x)也相同,则两梁的挠曲线形状一定相同。( )

3.梁上弯矩最大的截面,其挠度也最大,而弯矩为0的截面,其转角也为0。( )

4.梁在弯曲变形时,当某一截面内弯矩为0,而且此截面左右的弯矩异号,则此处定为挠曲线拐点。( )

5.等截面或分段等截面(阶梯状)梁,可用积分法求梁的位移,但变截面梁则不能用积分法求梁的位移。( )

二、选择题

1.如图7.6所示,已知梁的弯曲刚度EI为常数,今欲使梁的挠曲线在x=l/3处出现一拐点,则比值Me1/Me2为( )。

(A)2　(B)3　(C)1/2　(D)1/3

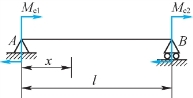
图7.6

2.外伸梁受载荷如图7.7所示,其挠曲线的大致形状为图7.8( )。

(A)(a)　(B)(b)　(C)(c)　(D)(d)

图7.7

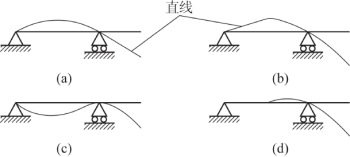
图7.8

三、填空题

1.试根据图7.9中载荷及支座情况,写出由积分法求解时,积分常数的数目及确定积分常数的条件:积分常数______________个,边界条件是________________,连续条件是________________。

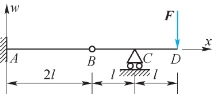
图7.9

2.写出图7.10所示变截面梁的挠曲线近似微分方程及确定积分常数的边界条件:微分方程是_____________________,边界条件是。

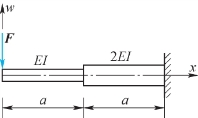
图7.10

四、计算题

1.试画出图7.11所示梁的挠曲线大致形状。

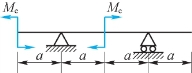(www.xing528.com)

图7.11

2.试画出图7.12所示等截面梁的挠曲线大致形状。

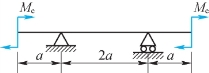
图7.12

3.试画出图7.13所示梁的挠曲线大致形状。

图7.13

【参考答案】

一、是非题

1.非 2.是 3.非 4.是 5.非

二、选择题

1.C 2.B

三、填空题

1.x=0,w1=0,w′1=0;x=3l,w2=0,w3=0,w′2=w′3;x=2l,w1=w2

2.

EIw″1=-Fx;2EIw″2=-Fx;x=a,w1=w2,w′1=w′2;x=2a,w2=0,w′2=0

四、计算题

1.挠曲线大致形状如图7.14所示。

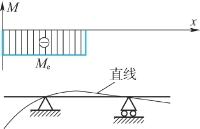
图7.14

2.挠曲线大致形状如图7.15所示。

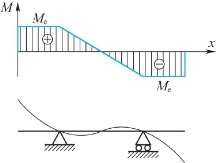
图7.15

3.挠曲线大致形状如图7.16所示。

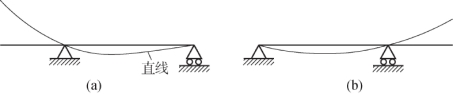
图7.16