基于切应力的强度条件和计算方法优化

对于各种形状的等直梁,其最大切应力一般都发生在最大剪力所在横截面上的中性轴处,并可写成统一表达式

式中:max为中性轴一侧半个截面对中性轴的静矩,b为横截面中性轴处的宽度。

在梁的强度计算中,必须同时满足梁的弯曲正应力和弯曲切应力两个强度条件。在工程中,通常是先按正应力强度条件选择截面尺寸,然后再进行切应力强度校核。

从前面的讨论知道,最大切应力发生在中性轴上,这里恰好正应力σ=0,所以可以像处理圆轴扭转一样来校核切应力,即

一般顺序是首先进行正应力强度条件校核,如果需要,再进行切应力校核。附录型钢表中给出了工字钢Iz∶S*

z的比值,进而可以计算工字钢的max。

【例6.6】一悬臂梁长为800 mm,在自由端受一集中力F的作用。梁由3块50 mm×100 mm的木板胶合而成,如图6.15所示,图中z轴为中性轴。胶合缝的许用切应力[]=0.35 MPa。试按胶合缝的切应力强度求许可载荷[F];并求在此载荷作用下,梁的最大弯曲正应力。

图6.15　例6.6图

【解】(1)易知梁各横截面上的剪力都等于F,可任取一横截面计算。由于两胶合缝关于中性轴对称,因此两胶合缝上的切应力相等,只需要计算其中一条即可。由(www.xing528.com)

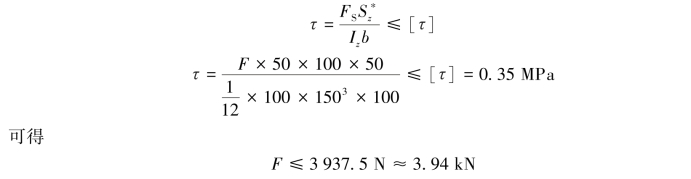
故许可载荷[F]=3.94 kN。

(2)易知梁的最大弯矩出现在固定端截面上,大小为Mmax=3.152 kN·m,由弯曲正应力公式可得

【例6.7】矩形截面梁如图6.16(a)所示,h=2b,许用应力[σ]=120 MPa,[]=50 MPa,试确定截面尺寸b、h。

【解】(1)求支反力,作剪力图与弯矩图,如图6.16(b)、(c)所示。

图6.16　例6.7图

(3)按弯曲切应力强度条件计算。由