纯弯曲条件下的正应力

二维码

在纯弯曲的情况下,梁的横截面上只有内力弯矩,故横截面上只有弯矩引起的正应力。在推导梁横截面上任一点的正应力的公式时,仍须综合考虑变形几何关系、物理关系和静力关系。

1.变形几何关系

取一矩形截面梁,在梁变形前,先在其表面画上一些垂直于轴线的横向线mm和nn,并在两横向线间靠近顶面和底面处分别画平行于轴线的纵向线aa、bb,如图6.2(a)所示。然后在梁两端纵向对称平面内,施加一对大小相等,转向相反的外力偶矩Me,使梁发生纯弯曲变形。变形后可观察到如下现象:

(1)所有横向线仍为直线,只是转过了一个微小的角度,且与弯曲后的轴线垂直;

(2)所有纵向线变成弧线,在正弯矩作用下,上部纵向线缩短,下部纵向线伸长。

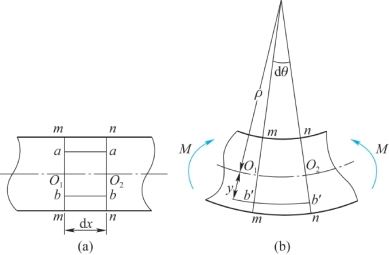
图6.2　纯弯曲及变形几何关系

根据观察到的以上实验现象,对梁内变形和受力作出如下假设:

(1)横截面在变形后仍保持为平面,且仍然垂直于变形后的梁轴线,只是绕横截面内某一轴转过了一个微小的角度,这就是弯曲变形的平面假设,或称平截面假设;

(2)设想梁是由许多相互平行的纵向纤维组成,变形后纤维之间互相不挤压,只受拉伸或压缩作用,这就是弯曲变形的纵向纤维单向受力假设。

由上面变形现象和假设可以知道梁变形后凹边一侧纤维缩短、凸边一侧纤维伸长,根据变形的连续性,中间必然有一层纤维的长度保持不变,这一层称为梁的中性层或称中性面。中性层与横截面的交线称为中性轴,如图6.3所示。梁在弯曲时,相邻横截面绕各自的中性轴在做相对转动。设梁的轴线为x轴,横截面对称轴为y轴,中性轴为z轴。显然,在平面弯曲时,中性轴z必然垂直于横截面的对称轴y轴。

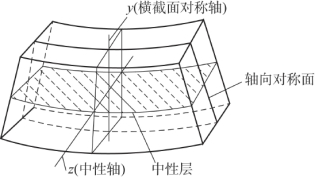
图6.3　纯弯曲梁的中性层、中性轴

下面研究纵向纤维的变化规律,用横截面m—m和n—n从梁中截取dx微段,如图6.2(a)所示,先分析距中性层为y处的某纵向纤维b′b′的线应变。

梁变形后,由平面假设可知m—m和n—n截面仍保持为平面,设此两横截面相对转角为dθ、中性层的曲率半径为ρ,如图6.2(b)所示,纵向纤维b′b′变形后的长度为

中性层纤维O1O2在梁变形后长度不变,所以O1O2=dx=ρdθ,由此得纵向纤维b′b′的线应变为

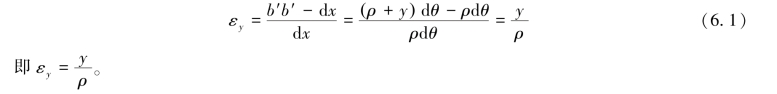(www.xing528.com)

在研究同一截面上不同点的正应力时,显然ρ为常量。因此,式(6.1)表明横截面上某点处的线应变与它到中性轴的距离y成正比。

2.物理关系

根据各纵向纤维单向受力假设,当材料在线弹性变形范围内时,应力、应变成正比例关系,即σ=Eε,由此得横截面上距中性层为y处的正应力σy为

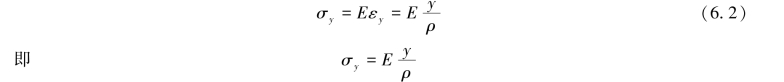
同理,式(6.2)表明横截面上距中性层为y处的正应力与该点到中性轴的距离y成正比,即正应力沿截面高度成线性规律变化,中性轴上各点处的正应力为0,离中性轴较远的上下边缘处正应力最大,如图6.4(a)所示。

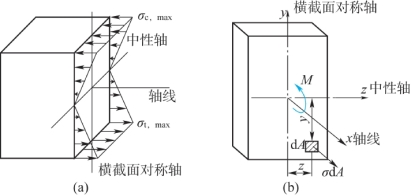
图6.4　弯矩与弯曲正应力之间的关系

3.静力关系

式(6.2)给出了正应力沿截面高度的分布规律,但因中性轴z的位置和中性层曲率半径ρ的大小均未知,所以尚不能用式(6.2)来计算正应力,这就需要考虑内力与应力之间的静力学关系。

如图6.4(b)所示,在横截面上取一微面积dA,其上的法向微内力为σydA,横截面上各点处的法向微内力组成一空间平行力系。这一力系可能简化成3个内力分量,即与x轴重合的轴力FN、对y轴力偶矩My、对z轴的力偶矩Mz,即

由于梁上仅有外力偶作用,因此由截面法,上式中的FN和My均等于0,Mz等于该横截面上的弯矩M,即

将式(6.2)代入式(6.3),得

式中:M为横截面上的弯矩;y为横截面上欲求点到中性轴的距离;Iz为横截面对中性轴z的惯性矩。

式(6.7)就是梁在纯弯曲时横截面上任意点处的正应力计算公式。

在式(6.7)中,将弯矩M和坐标y按规定的正负号代入,所得正应力若为正值,即为拉应力;若为负值,则为压应力。在具体计算时,也可不必考虑弯矩和坐标的正负号,直接代入其绝对值,再根据梁变形的情况判断所求点的正应力是拉应力还是压应力,即以中性层为界,凸边一侧的为拉应力,凹边一侧的为压应力。