【摘要】:如图5.17所示,设梁上作用分布载荷的集度为q,并规定向上为正。用梁上相距为dx的m—n和m1—n1两个截面切出一dx微段,分析它的平衡。因为要利用以上微分关系画图,所以要重点理解其对应的几何意义。由式(5.5)可知,弯矩图在一点x0处的切线的斜率等于剪力FS在该点处的值FS。图5.17载荷集度、剪力和弯矩间的微分关系根据以上的表述,可将其规律总结列入表5.1。
先来研究载荷集度、剪力和弯矩之间的微分关系。如图5.17(a)所示,设梁上作用分布载荷的集度为q(x),并规定向上为正。用梁上相距为dx的m—n和m1—n1两个截面切出一dx微段,分析它的平衡。设作用于m—n截面上的剪力FS(x)、弯矩M(x)均按正向假设,如图5.17(b)所示。设m1—n1截面上的内力在m—n截面上的内力基础上有相应的增量,即m1—n1截面上的剪力应为FS(x)+dFS(x),弯矩为M(x)+dM(x),也按正向假设,如图5.17(b)所示。对于q(x),由于dx很微小,因此近似地认为在dx段上是均匀分布。考虑dx微段的平衡,有

二维码

由式(5.4)、式(5.5)可知,将弯矩方程M(x)对x求一阶导数,即得剪力方程FS(x);将剪力方程FS(x)对x求一阶导数即得分布载荷集度q(x)。
将式(5.5)代入式(5.4),可得

由式(5.6)可知,将弯矩方程M(x)对x求二阶导数,即得分布载荷集度q(x)。(https://www.xing528.com)
因为要利用以上微分关系画图,所以要重点理解其对应的几何意义。
由式(5.5)可知,弯矩图在一点x0处的切线的斜率等于剪力FS(x)在该点处的值FS(x0)。由式(5.4)可知,剪力图在一点x0处的切线的斜率等于分布载荷集度q(x)在该点处的值q(x0)。
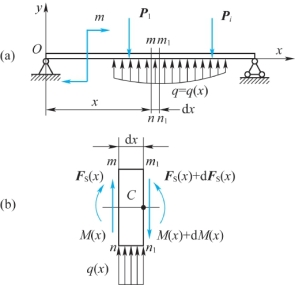
图5.17 载荷集度、剪力和弯矩间的微分关系
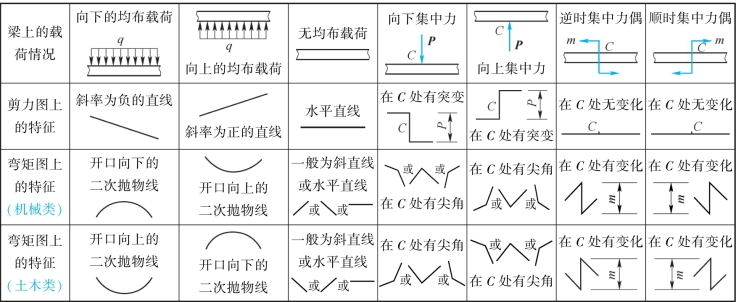
根据以上的表述,可将其规律总结列入表5.1。
表5.1 分布载荷集度、剪力和弯矩间的微分关系
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




