转换为：主惯性轴和矩阵的关系

由式(4.22)中的第三式可知,当一对正交坐标轴绕原点O转动时,其惯性积将随着α的改变而变化,其值可正、可负,也可为0。但总可以找到一特定角度α0以及相应的y0、z0轴,使图形对这一对坐标轴的惯性积为0。令

解得

另外,过形心的主轴称为形心主惯性轴,简称形心主轴,平面图形对于形心主轴的惯性矩称为形心主惯性矩。在工程实际中,形心主轴与形心主惯性矩更有工程意义。

对于形心主轴,可以归纳出以下几点结论。

(1)如果平面图形有一个对称轴,则该轴必是一个形心主轴,另一个形心主轴通过图形的形心且与该轴垂直,如图4.16(a)所示。

(2)如果平面图形有两个对称轴,则该两轴就是形心主轴,如图4.16(b)、(c)所示。

(3)如果平面图形有两个以上对称轴,则任一对称轴都是形心主轴,且截面对任一形心主轴的惯性矩都相等,如图4.16(d)、(e)、(f)所示。可推知,正多边形的任一形心轴皆为形心主轴,且图形对所有形心轴的惯性矩都相等。

图4.16　形心主轴与形心主惯性矩

如果图形没有对称轴,这时如何求得形心主轴及主惯性矩呢?下面通过例题说明。

【例4.11】试确定图4.17所示截面的形心主轴位置,并求形心主惯性矩。

图4.17　例4.11图

【解】(1)确定形心位置。

图示截面可视为由Ⅰ、Ⅱ、Ⅲ3个矩形所组成。由于截面形状为极对称,因此该截面的形心C与矩形Ⅱ的形心相重合。(www.xing528.com)

(2)计算截面对y、z轴的惯性矩和惯性积。

先选取建立参考轴系yCz,如图4.17所示。矩形Ⅰ、Ⅲ的形心在所选参考坐标系中的坐标为

利用组合截面计算公式和平行移轴公式(式(4.19))可得整个截面对z、y轴的惯性矩和惯性积分别为

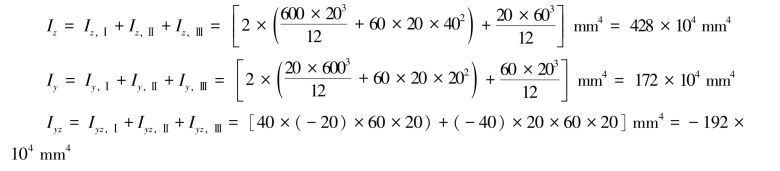
(3)确定形心主轴的位置。

将上述结果代入式(4.24),得

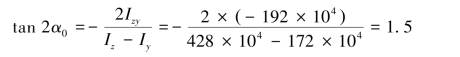
故

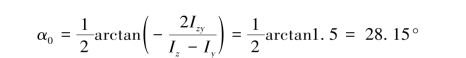
即表明将z轴、y轴分别逆时针转α0=28.15°,便分别得到形心主轴zα0和yα0。

(4)计算形心主惯性矩。

将Iz,Iy和Izy的值代入式(4.25),便得形心主惯性矩Imax和Imin。

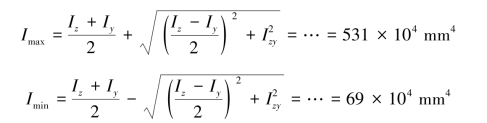
表4.1中给出了几种简单基本平面图形的常用几何性质。

表4.1　几种简单基本平面图形的常用几何性质