平行移轴公式的应用技巧及注意事项

二维码

利用惯性矩、惯性积的定义,容易求出简单形状截面对其形心轴的惯性矩和惯性积。但工程实际中的截面形式多样,有时需要计算截面对非形心轴的惯性矩和惯性积。同一平面图形对互相平行的两根轴的惯性矩并不相同,但它们之间存在一定的关系。本节讨论同一平面图形对两根互相平行的轴的惯性矩之间的关系以及惯性积之间的关系。

当两根互相平行的轴其中之一通过图形的形心时,它们之间存在比较简单的关系。如y轴与yC轴平行,yC轴通过形心;z轴与zC轴平行,zC轴通过形心,如图4.11所示。

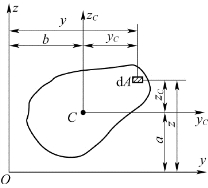
图4.11　惯性矩和惯性积的平行移轴公式

先将图形对yC和zC轴的惯性矩和惯性积记为

图形对y轴和z轴的惯性矩和惯性积分别为

设y轴与yC轴的平行间距为a,z轴与zC轴的平行间距为b,则由图4.11可得

将式(4.17)代入式(4.16)展开后得

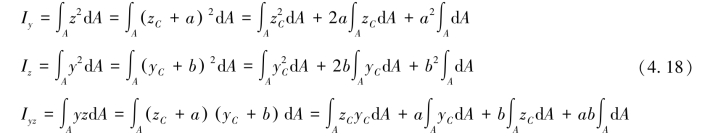
由定义可知

由于yC轴、zC轴是形心轴,因此静矩SyC=0、SzC=0,于是式(4.18)简化为

式(4.19)称为惯性矩和惯性积的平行移轴公式。应用平行移轴公式即可根据截面图形对其形心轴的惯性矩或惯性积,计算截面图形对于与形心轴平行的坐标轴的惯性矩或惯性积,或进行相反的推算。应用式(4.19)时的注意事项如下。

(1)两平行轴中应有一轴是过形心的,否则平行移轴公式不成立。因a2A和b2A恒大于0,所以平面图形对一系列平行轴的惯性矩中,以对形心轴的惯性矩最小。

(2)两个坐标轴必须平行,如果两轴之间有夹角,则要利用下一节中的转轴公式先转换,再使用平行移轴公式。(www.xing528.com)

(3)在计算惯性积Iyz时应特别注意:Iyz=IyCzC+abA,式中的a和b是平面图形形心C在yOz坐标系中的坐标值,因此a,b值是有正负的。

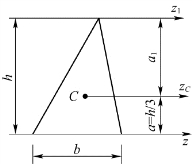
图4.12　例4.8图

【解】因平行移轴公式中的两轴之一必过形心,所以需过形心C作与z轴平行的zC轴。

由式(4.19)得

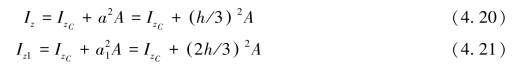
式(4.20)与式(4.21)相减得

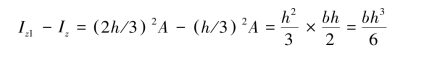
于是

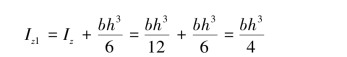
本题也可以先由式(4.20)求出IzC,再由式(4.21)计算Iz1。

【例4.9】求图4.13所示半径为r的半圆对平行于直径边的形心轴zC的惯性矩。

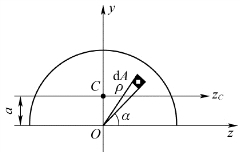
图4.13　例4.9图

由于对称性,半圆对z轴的惯性矩为整个圆对z轴惯性矩的一半,即

于是