惯性矩与惯性积的概念和计算

图4.5所示任意平面图形,其面积为A。在平面图形任意点(y,z)处取微面积dA,遍及整个图形面积A的积分为

式中:Iy、Iz分别定义为图形对y轴和z轴的惯性矩,也称为二次矩,其量纲为长度的4次方。

有时把惯性矩写成图形面积A与某一长度的平方的乘积,即

把iy和iz分别称为平面图形对y轴和z轴的惯性半径或回转半径,其量纲为长度的1次方。

在平面图形任意点(y,z)处取微面积dA,遍及整个图形面积A的积分为

式中:Iyz定义为图形对相互正交的y轴和z轴的惯性积,也是二次矩,其量纲为长度的4次方。

由图4.5可见,ρ2=y2+z2,可以得出惯性矩与极惯性矩之间的关系式

式(4.9)表明:截面对任意两个互相正交轴的惯性矩之和,等于它对该两轴交点的极惯性矩。

由式(4.5)~式(4.9)可得以下几点结论。

(1)同一图形对不同坐标轴的惯性矩(Iy、Iz)、惯性积Iyz和极惯性矩IP是不同的,它们的量纲都是长度的4次方。惯性矩和极惯性矩的值恒为正;惯性积的值可正可负,也可为0。

(2)惯性积Iyz为0的任一对正交轴(y轴、z轴)称为主惯性轴,简称主轴。

(3)若平面图形具有对称轴,且此对称轴又为正交坐标系中的一个坐标轴,则该平面图形对这一坐标系的惯性积必为0,下面举例说明。

图4.6　对称平面图形与惯性积

【例4.4】图4.7所示矩形的高为h、宽为b,试求矩形对其对称轴y和z的惯性矩。

【解】先求对y轴的惯性矩Iy。取如图所示的微面积dA=bdz,由惯性矩的定义可得

同理,求对z轴的惯性矩Iz。取如图所示的微面积dA=hdy,由惯性矩的定义可得

图4.7　例4.4图(www.xing528.com)

【例4.5】计算图4.8所示图形对其形心轴的惯性矩。

【解】以圆心为原点,取坐标轴如图4.8所示。

图4.8　例4.5图

由式(4.9)及对称性可知,圆截面对任一形心轴的惯性矩相等,则有

由式(4.5)、式(4.6)、式(4.8)可知:若一个平面图形由若干个简单基本图形组合而成,则在计算该组合图形对坐标轴的惯性矩和惯性积时,可以分别计算其中每一个简单基本图形对同一对坐标轴的惯性矩和惯性积,然后求其代数和,即

类似地,组合图形的极惯性矩计算式为

【例4.6】求图4.9所示上下、左右均对称的工字形截面对其对称轴z的轴惯性矩。

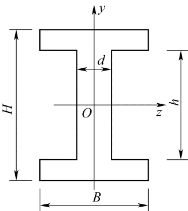
图4.9　例4.6图

【例4.7】试计算图4.10中矩形和圆形对形心y轴、z轴的惯性半径。

图4.10　例4.7图

【解】图4.10(a)矩形:由【例4.4】的结果,可知

由式(4.7b)得,矩形对形心y轴、z轴的惯性半径为

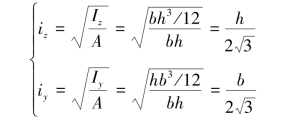
图4.10(b)圆形:已知圆形过形心的任一轴惯性矩为

于是,圆形对形心y轴、z轴的惯性半径为