探究形心和静矩的相关概念

杆件的横截面是一个平面图形,现取任意平面图形,设其面积为A,如图4.1所示。平面图形的几何中心C称为形心。若将此平面图形视为均质等厚的超薄板,由静力学可知,该薄板重心、质心和薄板图形的形心三者在Oyz平面内重合,在yOz坐标系中,取平面图形任意点(y,z)处微面积dA,则该薄板的重心、质心、形心在yOz坐标系中的坐标为

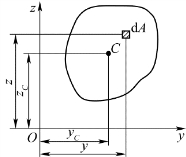
图4.1　任意横截面图形及形心和静矩的定义

二维码

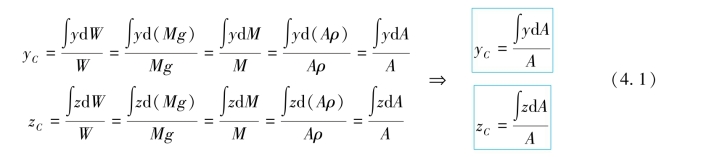
式(4.1)即为计算平面图形形心C的坐标公式。其中的两个积分项写为

式中:Sy、Sz分别定义为平面图形对于y轴和z轴的静矩(平面矩),也称为一次矩。

由式(4.1)和(4.2)可以得出静矩与形心的关系式

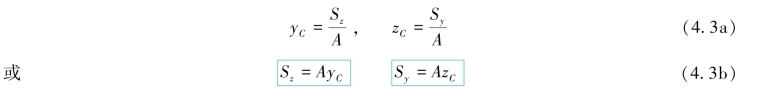
由式(4.1)~式(4.3)可以得出以下几点结论。

(1)截面的静矩是对某一坐标轴而言的,同一图形对不同坐标轴有不同的静矩,其值可正可负,也可为0。静矩的量纲为长度的三次方。

(2)若某一坐标轴通过平面图形的形心,则该轴称为平面图形的形心轴,平面图形对形心轴的静矩必等于0。反之,若平面图形对某轴的静矩等于0,则该轴必为此平面图形的形心轴。

(3)若平面图形有对称轴,则形心必在该对称轴上。因此,平面图形对其对称轴的静矩必为0。(www.xing528.com)

【例4.1】试计算图4.2所示等腰三角形ABD对y轴和z轴的静矩,并确定其形心位置。

【解】由于z轴为等腰三角形ABD的对称轴,故有

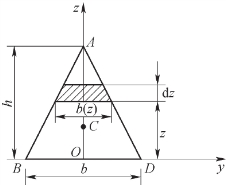
图4.2　例4.1图

根据静矩的定义,可将该三角形分割为若干个平行于y轴的微面积元,如图4.1中的阴影部分。由相似三角形的几何关系知

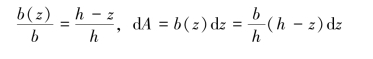
由式(4.2),有

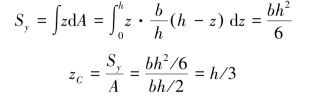
【例4.2】已知半圆的半径为R。求图4.3所示半圆截面的静矩Sy、Sz及形心C位置。

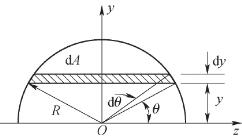
图4.3　例4.2图

【解】(1)求静矩。由于y轴为对称轴,故有