思3.1 剪切变形的受力特点与变形特点是什么?请举出两个剪切变形的实例。
思3.2 何谓工程实用计算,工程实用计算的依据是什么?
思3.3 在减速箱中常看到高速轴的直径较小,而低速轴的直径较大,这是为什么?
思3.4 圆轴扭转切应力公式是如何建立的?该公式的应用范围是什么?
思3.5 扭转切应力在横截面上是如何分布的?
思3.6 两根材料相同、长度相同及横截面积相等的圆轴,一根是实心的,另一根是空心的,在相同扭矩作用下,最大切应力和单位长度扭转角是否相等?
思3.7 直径和长度均相同而材料不相同的两根轴,在相同外力偶作用下,它们的最大切应力和相对扭转角是否相同?
思3.8 如果轴的直径增大一倍,其他情况不变,那么最大切应力和相对扭转角将怎样变化?
思3.9 根据圆轴扭转的平面假设,是否可以认为圆轴扭转时其横截面形状尺寸不变,直径仍为直线?
思3.10 直径为D的实心圆轴,两端受扭转力偶矩作用,轴内最大切应力为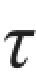
,若轴的直径改为D/2,则轴内的最大切应力变为多少?
思3.11 当实心圆轴的直径增加1倍时,其抗扭强度、抗扭刚度分别增加到原来的多少倍?
思3.13 从受扭圆轴内截取虚线所示形状部分,则该部分哪个面上无切应力?
思3.14 受扭圆轴上贴有3个应变片,如图所示。实测时哪个应变片的读数几乎为0?
思3.13图
思3.14图
【3.1类】计算题(剪切和挤压的实用计算)
题3.1.1 请校核图示拉杆头部的剪切强度和挤压强度。已知图中尺寸D=32 mm,d=20 mm和h=12 mm,杆的许用切应力[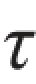
]=100 MPa,许用挤压应力[σbs]=240 MPa。
题3.1.2 图示两个铆钉将140 mm×140 mm×12 mm的等边角钢铆接在立柱上,构成支托。若F=30 kN,铆钉的直径d=21 mm,试求铆钉的切应力和挤压应力。
题3.1.1图
题3.1.2图
题3.1.3 矩形截面木拉杆的接头如图所示。已知轴向拉力F=50 kN[或: ],截面的宽度b=250 mm,木材顺纹的许用挤压应力[σbs]=10 MPa,顺纹的许用切应力[
]=1 MPa。试确定接头处所需的尺寸l和a。
题3.1.4 如图所示,在桁架的支座部位,斜杆以宽度b=60 mm的榫舌和下弦杆连接在一起。已知木材顺纹许用挤压应力[σbs]=5 MPa,顺纹许用切应力[
]=0.8 MPa[或: ],作用在桁架斜杆上的轴向压力F=20 kN。试按强度条件确定榫舌的高度δ(即榫接的深度)和下弦杆末端的长度l。
题3.1.3图
题3.1.4图
题3.1.5 图示两块钢板用4个铆钉连接在一起,板厚δ=20 mm,宽度b=120 mm,铆钉直径d=26 mm,钢板的许用拉应力[σt]=160 MPa,铆钉的许用切应力[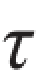
]=100 MPa[或: ],铆钉的许用挤压应力[σbs]=280 MPa,试求此铆钉接头的最大许可拉力。
题3.1.6 图示为由两个螺栓连接的接头。已知F=40 kN,螺栓的许用切应力[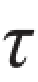
]=130 MPa[或: ],许用挤压应力[σbs]=300 MPa。试求螺栓所需的直径d。
题3.1.5图
题3.1.6图
题3.1.7 图示正方形截面的混凝土柱横截面边长为200 mm,其基底为边长a=1 m[或: ]的正方形混凝土板。柱承受轴向压力F=100 kN。假设地基对混凝土板的支反力为均匀分布,混凝土的许用切应力为[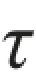
]=1.5 MPa,试问为使柱不穿过基底板,混凝土板所需的最小厚度δ应为多少?
※题3.1.8 图示凸缘联轴节传递的力偶矩为Me=200 N·m,凸缘之间用4根螺栓连接,螺栓内径d=10 mm[或: ],对称地分布在直径为D0=80 mm的圆周上。如螺栓的剪切许用应力[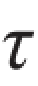
]=60 MPa,试校核螺栓的剪切强度。
题3.1.7图
题3.1.8图
※题3.1.9 图示机床花键轴有8个齿。轴与轮的配合长度l=60 mm,外力偶矩Me=4 kN·m[或: ]。轮与轴的挤压许用应力为[σbs]=140 MPa,试校核花键轴的挤压强度。
【3.2类】计算题(外力偶矩的换算、求扭矩、绘制扭矩图)(www.xing528.com)
题3.2.1 传动轴转速n=300 r/min[或: ],主动轮A输入功率PA=60 kW,3个从动轮B、C、D的输出功率分别为PB=10 kW,PC=20 kW,Pd=30 kW,如图所示。试求各指定截面上的内力扭矩,并绘该轴的扭矩图。
题3.1.9图
题3.2.1图
【3.3类】计算题(计算扭转应力、强度计算和求变形、刚度计算)
题3.3.1 如图所示,圆轴截面直径d=50 mm,圆轴两端受Me=1 kN·m的外力偶矩的作用,材料的切变模量G=80 GPa。试求:(1)横截面上半径ρA=d/4[或: ],点A处的切应力和切应变;(2)该截面上最大切应力和该轴的单位长度扭转角。
题3.3.2 圆轴的直径d=50 mm,转速为n=120 r/min。若该轴横截面上的最大切应力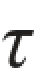
max=60 MPa[或: ],试问所传递的功率P为多大?
题3.3.3 一空心圆轴的外径D=90 mm,内径d=60 mm[或: ]。试计算该轴的抗扭截面系数WT,若在横截面积不变的情况下,改用实心圆轴,试比较两者的抗扭截面系数。
题3.3.4 空心钢轴的外径D=100 mm,内径d=50 mm。已知该轴上间距为l=2.7 m的两横截面的相对扭转角φ=1.8°[或: ],材料的切变模量G=80 GPa。试求:(1)轴内的最大切应力;(2)当轴以n=80 r/min的转速旋转时,轴所传递的功率。
题3.3.5 图示外径D=200 mm的圆轴,AB段为实心,BC段为空心,且内径d=50 mm,已知材料许用切应力为[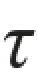
]=50 MPa[或: ],求Me的许可值。
题3.3.1图
题3.3.5图
题3.3.6 已知空心圆轴的外径D=76 mm,壁厚δ=2.5 mm,承受外力偶矩Me=2 kN·m作用,材料的许用切应力[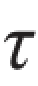
]=100 MPa,切变模量G=80 GPa,许可单位扭转角[θ]=2(°)/m[或: ]。试:(1)校核此轴的强度和刚度;(2)如改用实心圆轴,且使强度和刚度保持不变,试设计轴的直径。
题3.3.7 图示一外径D=50 mm,内径d=30 mm的空心钢轴,在扭转力偶矩Me=1 600 N·m的作用下,测得相距200 mm的A、B两截面间的相对转角φ=0.4°[或: ],已知钢的弹性模量E=210 GPa。试求材料的泊松比μ。
题3.3.8 图示一等直圆杆,已知d=40 mm,a=400 mm,G=80 GPa,φBD=1°[或: ]。试求:(1)最大切应力;(2)截面A相对于截面C的扭转角φAC。
题3.3.7图
题3.3.8图
题3.3.9 图示直径d=50 mm的等直圆杆,在自由端承受一外力偶矩Me=1.2 kN·m时,在圆杆表面上的B点移动到了B1点。已知:l=6 m,Δs=BB1=6.3 mm[或: ],材料的弹性模量E=200 GPa。试求钢材的弹性常数G和μ。
※题3.3.10 如图所示,长度相等的两根受扭圆轴,一为空心圆轴,一为实心圆轴,两者材料相同,受力情况也一样。实心轴直径为d;空心轴外径为D,内径为d0,且d0/D=0.8[或: ]。试求当空心轴与实心轴的最大切应力均达到材料的许用切应力(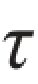
max=[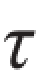
]),扭矩T相等时的重量比和刚度比。
题3.3.9图
题3.3.10图
※题3.3.11 由两人操作的绞车如图所示。若两人作用于手柄上的力都是P=200 N,已知轴的许用应力[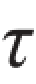
]=40 MPa,试按照强度要求估算AB轴的直径,并确定最大起重量Q。
题3.3.11图
※题3.3.12 有一壁厚δ=25 mm[或: ]、内径d=250 mm的空心薄壁圆管,其长度l=1 m,作用在轴两端面内的外力偶矩Me=180 kN·m。材料的切变模量G=80 GPa。试确定管中的最大切应力,并求管内的应变能。
【3.4类】计算题(扭转超静定问题)
※题3.4.1 如图所示,阶梯形圆形组合实心轴,在A、C两端固定,B端面处作用外力偶矩Me=900 N·m[或: ],相应段的长度、直径、切变模量分别为:l1=1.2 m,l2=1.5 m,d1=25 mm,d2=37.5 mm,G1=80 GPa,G2=40 GPa。试求该组合实心轴中的最大切应力。
【3.5类】计算题(非圆截面杆扭转)
☆题3.5.1 如图所示,矩形截面杆受Me=3 kN·m[或: ]的一对外力偶作用,材料的切变模量G=80 GPa。求:(1)杆内最大切应力的大小、位置和方向;(2)横截面短边中点的切应力;(3)单位长度扭转角。
题3.4.1图
题3.5.1图
☆题3.5.2 如图所示,一等厚闭口薄壁杆,两端受扭转力偶作用,杆的最大切应力为60 MPa[或: ]。求:(1)扭转力偶矩Me;(2)在杆上沿母线切开一条缝AB,开口后扭转力偶矩。
☆题3.5.3 如图所示,一个T形薄壁截面杆,长L=2 m,在两端受扭转力偶作用,杆的扭矩T=0.2 kN·m,材料的切变模量G=8×104 MPa,求此杆在自由扭转时的最大切应力及扭转角。
题3.5.2图
题3.5.3图
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
