闭口薄壁杆件自由扭转浅析

3.5节中介绍的薄壁圆筒扭转,其壁厚不变,本节所介绍的闭口薄壁截面杆件,其壁厚是可变的。类似于薄壁圆筒,闭口薄壁截面杆件自由扭转时,横截面上的切应力沿厚度也是均匀分布,方向与周边或截面中线相切。

图3.25　闭口薄壁杆件的自由扭转

式中:ρ为点O到截面中线切线的垂直距离;ρds等于图3.25(a)中阴影线三角形面积的2倍,故其沿壁厚中线全长s的积分应是该中线所围面积A0的2倍。于是,可得

闭口薄壁截面等直杆的单位长度扭转角φ′可按功能原理来求得。

由纯剪切应力状态下的应变能密度u的表达式(3.30)及式(3.42),可得杆内任一点处的应变能密度为

又根据应变能密度u计算扭转时杆内应变能的表达式(3.30),可得单位长度杆内的应变能为

式中:V为单位长度杆壁的体积,dV=1×δ×ds=δds。

将dV代入式(3.44),并沿壁厚中线的全长s积分得

然后,计算单位长度杆两端截面上的扭矩对杆段的相对扭转角φ′所做的功。由于杆件在线弹性范围内工作,因此所做的功应为

(www.xing528.com)

式(d)和式(e)中的U和W在数值上相等,从而解得

式中:积分取决于杆的壁厚δ沿壁厚中线s的变化规律。

当壁厚δ为常数时,则得

式中:s为壁厚中线的全长。

【例3.10】图3.26(a)、(b)为相同材料和相同截面的两正方形薄壁截面杆,其中图3.25(b)沿杆纵向切开一缝,两杆受相同外力偶矩Me作用,已知b=50 mm和δ=2 mm。试求两杆的最大切应力之比。

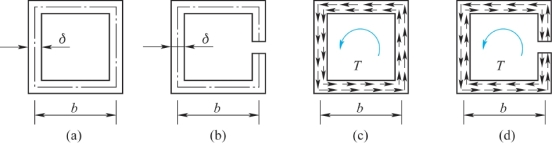
图3.26　例3.9图

【解】图3.26(a)为闭口薄壁截面杆,其切应力分布规律如图3.26(c)所示,由截面法得最大切应力按式(3.43)计算,其值为

图3.26(b)为开口薄壁截面杆,其切应力分布规律如图3.26(d)所示,最大切应力按式(3.40)计算,其值为

因此有

结果表明:相同截面在相同外力偶作用下,开口截面上的最大切应力是闭口截面上最大切应力的37.5倍。