非圆截面直杆扭转的定义及特点

前面各节讨论了圆形截面杆的扭转。但有些受扭构件的横截面并非圆形。例如,农业机械中有时采用方轴作为传动轴;又如,曲轴承受扭转的曲柄,其横截面是矩形的。

在分析等直圆杆扭转中其横截面上的应力时,主要依据为平面假设。对于等直非圆截面杆,扭转时其横截面不再保持为平面。取一横截面为矩形的杆,在其侧面画上纵向线和横向周界线,如图3.20(a)所示;扭转变形后发现横向周界线已变为空间曲线,如图3.20(b)所示。这表明变形后杆的横截面已不再保持为平面,这种现象称为翘曲。所以,平面假设对非圆截面杆的扭转已不再适用,这类问题只能用弹性理论方法求解。

图3.20　等直非圆杆扭转

非圆截面杆的扭转可分为自由扭转和约束扭转。如果扭转时杆横截面的翘曲不受任何约束,则称为自由扭转,此时各横截面的翘曲程度相同,横截面上只有切应力而无正应力。若因受力或约束条件的限制,使扭转各横截面的翘曲程度不同,则称为约束扭转,这时两相邻截面间纵向线段的长度有改变,故横截面上除了有切应力外还有正应力。一般情况下,实体杆件在约束扭转时的正应力很小,通常不予考虑,但对于薄壁截面杆的约束扭转,其横截面上的正应力较大而不可忽略。

非圆截面杆的自由扭转,一般在弹性力学中讨论。这里我们不加推导地引用弹性力学的一些结果,并只限于矩形截面杆扭转的情况。矩形截面杆扭转时,横截面上的切应力分布如图3.21(a)所示。此时,杆件横截面上的切应力分布具有如下特点:

(1)截面边缘各点的切应力形成与边界相切的顺流;

(2)4个角点上的切应力等于0;

(3)最大切应力发生在矩形长边的中点处,为

式中:WT仍称为扭转截面系数;h和b分别代表矩形截面长边和短边的长度;α是一个与比值h/b有关的系数,其数值如表3.1所示。

短边中点的切应力1是短边上的最大切应力,为

式中: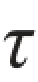max是长边中点的最大切应力;系数ν与比值h/b有关,其值如表3.1所示。

杆件两端相对扭转角

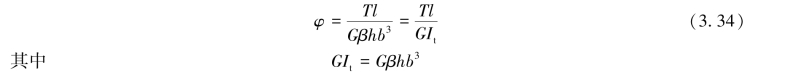
式中:It称为截面的相当极惯性矩;GIt称为非圆截面杆件的抗扭刚度;β也是与比值h/b有关的系数,其值如表3.1所示。(www.xing528.com)

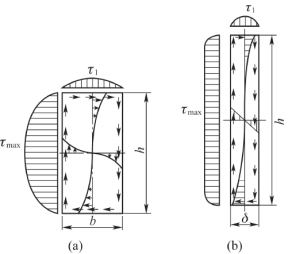
图3.21　矩形截面杆扭转的切应力分布

表3.1　矩形截面杆扭转时的系数α、β和ν

在狭长矩形截面上,扭转切应力的变化情况如图3.21(b)所示。虽然最大切应力在长边的中点,但沿长边各点的切应力实际上变化不大,接近相等,在靠近短边处才迅速减小为0。

【例3.9】一受扭矩形截面杆,截面高和宽分别为h=100 mm和b=50 mm。已知截面上的扭矩T=4 kN·m。(1)试计算截面上的最大切应力;(2)在横截面积不变的条件下,将矩形截面改变为圆形截面,试比较两者的最大扭转切应力。

【解】(1)由h/b=100/50=2.0,从表3.1查得α=0.246。

由式(3.32)得

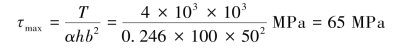
(2)依题意,直径为D的圆截面面积A为

由此解得

则圆轴的最大扭转切应力为

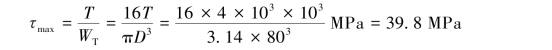
可见,在横截面积相等的条件下,矩形截面杆扭转产生的最大切应力要比圆截面杆扭转产生的最大切应力大得多。