横截面应力分析：原理与方法

二维码

与薄壁圆筒相仿,在小变形条件下,圆轴在扭转时横截面上也只有切应力而无正应力。为求得圆轴在扭转时横截面上的切应力计算公式,需先从变形几何方面和物理关系方面求得切应力在横截面上的分布规律,然后再考虑静力学方面来求解。

1.变形几何方面

为了观察圆轴的扭转变形,在圆轴的表面上作出任意两个相邻的圆周线和纵向线(在图3.12(a)中,变形前的纵向线用细点画线表示)。在圆轴两端施加一矩为Me的外力偶后,可以发现:各圆周线绕轴线相对地旋转了一个角度,圆周线的大小和形状均未发生改变;在小变变形的情况下,圆周线间的间距也未变化,纵向线则倾斜了一个角度γ。变形前表面的矩形方格abcd变形后错动成为平行四边形a′b′c′d′。

图3.12　圆轴扭转变形的几何关系放大图

根据所观察到的现象,可作如下假设:圆轴扭转变形前后,其横截面始终保持为平面,形状和大小不变,半径射线均保持为直线,且相邻两横截面间的距离不变。这就是圆轴扭转的平面假设或称平截面假设。按照这一假设,横截面如同刚性平面般绕圆轴的轴线转动。试验和弹性力学理论指出:在圆轴扭转变形后只有等直圆轴的圆周线才仍在垂直于轴线的平面内。所以,上述假设只适用于等直圆轴。

为确定横截面上任意一点处的切应力随点位置的变化规律,假想地用相邻的横截面p—p和q—q从轴中取出长为dx的微段进行分析,并放大为图3.12(b)。若截面q—q对截面p—p的相对扭转角为dφ,则根据平面假设,横截面q—q上的任意的半径Oa也转过了角度dφ到了Oa′。由于截面转动,因此圆轴表面上的纵向线da倾斜了一个角度γ。纵向线的倾斜角γ就是横截面周边上任一点d处的切应变(或剪应变)。根据平面假设,用相同的方法并参考局部放大图3.12(c)、(d),可以求得圆轴横截面上距圆心为ρ处的切应变为

以ρ表示横截面上距圆心为ρ处的切应力,则由剪切胡克定律可知,在线弹性范围内,切应力与切应变成正比,由式(3.9)知

式(c)表明横截面上任一点的切应力ρ与该点到圆心的距离ρ成正比。ρ的方向应垂直于半径,因为γρ是垂直于半径平面内的切应变。切应力沿任一半径的变化情况如图3.13所示。

式(a)表示圆轴横截面上任一点处的切应变随该点在横截面上的位置而变化的规律,如图3.12(e)所示。对于受力一定的圆轴而言,其变形程度是一定的,表示单位长度的相对扭转角的dφ/dx是一个常量。因此,在同一半径ρ的圆周上各点处的γρ均相同,且与ρ成正比。

2.物理关系方面

图3.13　切应力沿任一半径的变化情况

3.静力学方面

横截面上切应力变化规律表达式(c)中的dφ/dx是个待定参数,为确定该参数,可考虑静力学。如图3.13所示,由于在横截面上任一直径上距圆心等距的两点处的微内力ρdA等值而方向相反,因此整个横截面上的微内力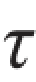ρdA的合力必为0,并且组成一个力偶,即为横截面上的扭矩T。由于ρ的方向垂直于半径,故微内力ρdA对圆心的力矩为ρρdA。于是,由静力学中的合力矩原理可得

将式(c)代入式(d),经整理后即得

式(e)中,积分∫Aρ2dA仅与横截面的几何形状及尺寸有关,称为横截面对圆心O点的极惯性矩,并用IP表示,即(www.xing528.com)

其量纲为长度的4次方。将式(3.11)代入式(e)并整理,得

将式(3.11)及式(3.12)代入式(e),得

式(3.13)即为圆轴扭转时横截面上任一点处切应力的计算公式。

由式(3.13)及图3.13可见:当ρ等于横截面的半径R时,即在横截面周边上的各点处,切应力将达到其最大值max,即

上式中,令WT=IP/R,则有

式中,WT(或用WP)称为抗扭截面系数或称抗扭截面模量,其量纲为长度的3次方。

推导切应力计算公式的主要依据是平面假设,且材料符合胡克定律。因此,上述诸公式仅适用于在线弹性范围内的等直圆轴。

为了计算截面对圆心的极惯性矩IP和抗扭截面系数WT,在圆截面上距圆心为ρ处取厚度为dρ的环形面积作为微元面积(见图3.14(a)),并由式(3.11)可得实心圆截面对圆心O的极惯性矩

实心圆截面的抗扭截面系数

图3.14　极惯性矩IP和抗扭截面系数WT

空心圆抗扭截面系数