用变形比较法求解简单杆系超静定问题

一、是非题

任何结构中,若其支座反力数目等于独立平衡方程式数目,则一定是静定结构。( )

二、选择题

1.图2.32所示结构中,杆AB和CD均为刚性杆,则此结构为( )结构。

(A)静定　(B)一次超静定

(C)二次超静定　(D)三次超静定

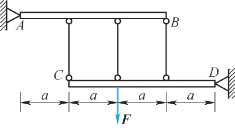
图2.32

2.图2.33所示结构中,杆AB为刚性杆,设Δl1、Δl2、Δl3分别表示杆1、2、3的伸长,则当求解杆1、2、3的内力时,相应的变形协调条件为( )。

(A)Δl3=2Δl1+Δl2(B)Δl2=Δl3-Δl1

(C)2Δl2=Δl1+Δl3(D)Δl3=Δl1+2Δl2

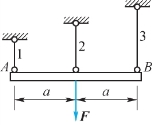
图2.33

三、填空题

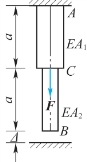
图2.34

2.材料和截面尺寸均相同的三杆与刚性杆AB铰接,受力如图2.35所示,三杆之间正应力的关系应为:σ′________σ″________σ‴(填入符号＜,=,＞)。其中σ′、σ″、σ‴分别为杆1、2、3的正应力。

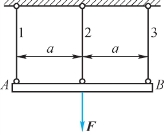
图2.35

四、计算题

1.一结构如图2.36所示,梁AB为刚性梁,B处作用集中力F,杆1、2、3的材料和横截面积皆相同。试求三杆的轴力。

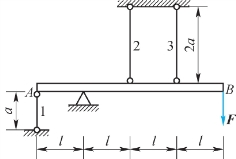
图2.36

2.图2.37所示结构中,杆AD为刚性杆,已知作用于点D的铅直力F=60 kN,杆1和杆2的材料和横截面积相同,且两杆的弹性模量E1=E2=E=200 GPa,横截面积A1=A2=A=100 mm2,杆2的长度a=1 m。试求:(www.xing528.com)

(1)杆1和杆2的内力;

(2)点D的铅直位移。

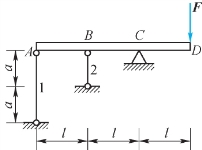
图2.37

【参考答案】

一、是非题

非

二、选择题

1.B 2.C

三、填空题

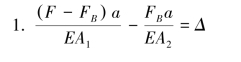
2.=,=

四、计算题

1.结构受力如图2.38所示。

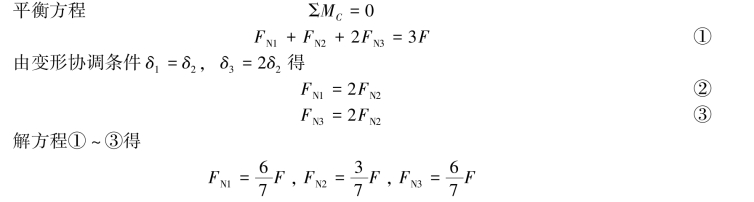
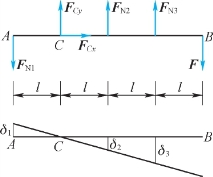
图2.38

2.结构受力如图2.39所示。

(1)平衡方程

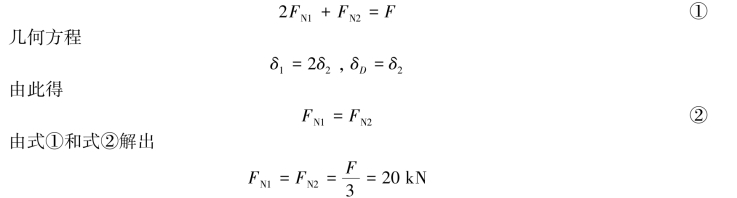
(2)由几何方程可得点D的铅直位移

图2.39