斜截面应力分析

前面讨论的是轴向拉伸与压缩时横截面上的正应力计算,它是强度计算的依据。实际工程应用中,有些拉(压)杆的破坏并不总是沿着横截面发生的,有时是沿着斜截面发生的,因此需要进一步讨论斜截面上的应力。

图2.12(a)为一轴向拉伸的等直杆,设其横截面积为A,则横截面(见图2.12(b))的正应力为

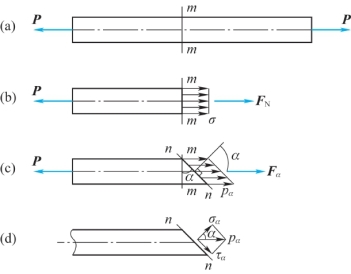
图2.12　α斜截面上应力

现假设沿与横截面成α角的斜截面(通常将斜截面称为α斜截面)将杆件截成两部分,如图2.12(c)所示。α符号的规定:由横截面外法线转至斜截面外法线逆时针转向取正,反之取负。

设α斜截面面积为Aα,则Aα与横截面积A之间的关系为

若取左段为研究对象(见图2.12(c)),设α斜截面上的内力合力为Fα,则

进一步观察图2.10的实验,可知任意两个相互平行的斜截面之间的纤维伸长量也是相等的,则α斜截面上的应力也是均匀分布的。由1.4节可知,α斜截面上的全应力(见图2.12(c))为

将全应力pα正交分解为两个分量,一个是α斜截面上的正应力σα(沿法线方向),一个是α斜截面上的切应力α(沿切线方向),如图2.12(d)所示,则其大小分别为

从式(2.6)和式(2.7)不难看出,α斜截面上的正应力σα和切应力α都是α的函数式,若α从0~2π变化一周,即考查了任一点的各方位的应力情况,这种通过一点的所有方位截面上应力情况的总和称为一点的应力状态。

讨论:对于轴向拉压情形,当α=0°时(横截面),σ0°=σ,0°=0;α=45°时,σ45°=σ/2,45°=max=σ/2,取得最大值;α=90°时(纵截面),σ90°=0,90°=0。

【例2.2】某阶梯轴受力如图2.13所示,P=10 kN,AB段的横截面积为A1=1 000 mm2,BC段横截面积为A2=500 mm2。试求:(1)AB、BC段横截面上的正应力;(2)AB段上与杆轴线成45°斜截面上的正应力和切应力;(3)杆内绝对值最大切应力,并指出截面所在杆段的位置。

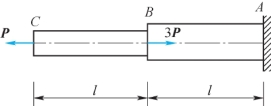
图2.13　例2.2图

【解】(1)用截面法分别求出AB段和BC段的轴力。

利用式(2.5)分别求出AB段和BC段横截面上的正应力。(www.xing528.com)

(2)求AB段上与杆轴线成45°角斜截面上的正应力和切应力。

利用式(2.6)与式(2.7)得

(3)求杆内的绝对值最大切应力,并指出截面所在杆段的位置。

AB段的绝对值最大切应力为

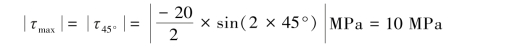
BC段的绝对值最大切应力为

所以,AB段和BC段的绝对值最大切应力相等,均为10 MPa。

【例2.3】矿井起重机钢绳如图2.14(a)所示,AB段横截面积A1=300 mm2,BC段横截面积A2=400 mm2,钢绳的单位体积重量γ=28 kN/m3,长度l=50 m,起重量P=12 kN,试求:(1)作轴力图(考虑钢绳自重);(2)钢绳内的最大正应力。

图2.14　例2.3图

【解】(1)作轴力图。

在图2.14(c)所示FN-x坐标下,由式(a)、(b)知FN(x)随x呈直线变化。由3个控制面上控制值FNA、FNB、FNC画出由两段斜直线构成的轴力图。

(2)钢绳内的最大正应力。

在可能的危险截面B面、C面截开(见2.14图(b)),有

所以σmax=σB=41.4MPa。

注意:等直杆件因轴向自重作用而引起的轴力图为一斜直线,本题中由于AB段与BC段横截面尺寸不同,因此轴力图由两条斜直线构成,只画成一条斜线是不对的。