
二维码
物体受到外力作用而变形时,其内部各质点之间的相对位置会发生变化,相应地,各质点间的相互作用力也随之发生变化。这种由外力作用引起的质点间相互作用力的改变,就是材料力学中所要研究的内力。由于假设物体是均匀连续的可变形固体,因此在物体内部相邻两部分之间相互作用的内力,实际上是一个连续分布的内力系,而将分布内力系的合成(力或力偶),简称为内力。简言之,内力是指在外力作用下,构件内部相邻部分之间分布内力系的合成,而非分子之间的凝聚力。内力与构件的强度、刚度、稳定性密切相关,所以在研究构件各种基本变形时,应当首先研究内力。
当外力沿着杆件的轴线作用时,其横截面上将产生沿轴线方向的内力,其内力的合力,用FN来表示,习惯上称为轴力。为了显示这种内力,用m—m横截面假想地把杆件分为两部分(见图2.6(a)),然后研究其中任意部分的平衡,求出轴力的大小和方向。根据作用与反作用定律可知,杆件左右两段在横截面m—m处的轴力必然等值反向(见图2.6(b)、图2.6(c))。

图2.6 截面法与受力图及轴力符号规定
材料力学中,轴力的正、负号的规定:使杆件产生拉伸变形的轴力为正,产生压缩变形的轴力为负。这样,无论取左段或右段为研究对象,可以保证同一个截面所得轴力不仅数值相等,而且符号一致。轴力的大小可以由横截面左段或右段的平衡条件来确定。
如在图2.6中取左段Ⅰ为研究对象(也可取右段Ⅱ),受力图如图2.6(b)所示,且将轴力按正向规定画出,则由(https://www.xing528.com)
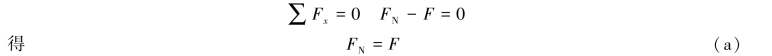
上述计算杆件横截面上的轴力的过程称为截面法,其计算步骤简单归纳如下。
(1)截开。用假想横截面将杆件从待求轴力截面处断开。
(2)代替。保留其中任意部分为研究对象,分析受力。注意在截开的横截面处,一般用正向规定表示的轴力代替截掉部分对保留部分的作用力。
(3)平衡。建立保留部分的平衡条件,求解轴力。应该注意,截开面上的内力对留下部分而言属于外力。
在应用截面法时需要注意以下两点。
(1)外载荷不能沿其作用线移动。因为材料力学中研究的对象是可变形体,不是刚体,所以力的可传递性不成立。
(2)截面不能切在外载荷作用点处,要离开或稍微离开作用点处。依据圣维南原理,力作用在构件某一位置上的方式不同,只会影响与作用点距离不大于构件横向尺寸的范围。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




