全向摄像机的标定方法优化

由一个透视摄像机和其正前方的反射镜面构成的全向摄像机称为反射折射摄像机，可以分为中心反射折射摄像机和非中心反射折射摄像机。其中，中心反射折射摄像机所成像容易反投到空间，得到场景的三维信息，因此在实际中有着很广泛的应用。中心反射折射摄像机的反射镜面可分为4种类型：抛物镜面、双曲镜面、椭球镜面和平面镜。众所周知，只有透视摄像机和其正前方反射镜面的光轴在一条直线上才能构成标准的中心反射折射摄像机。本章提及到的全向摄像机均指中心反射折射摄像机。

1）全向摄像机成像模型

2001年，Geyer等提出所有全向成像过程都等价于一个经过单位球的两步成像模型（见图6－26）：首先，空间点经过透视摄影到以反射镜面焦点为中心的单位球上的点Xs＝（xs ys zs）T；然后，以空间点Oc为投影中心将Xs投影到与直线O Oc垂直的平面Π上，从而形成图像点m，其中Oc称为虚拟摄像机光心，O称为视球中心。以O为原点的坐标系为摄像机坐标系。

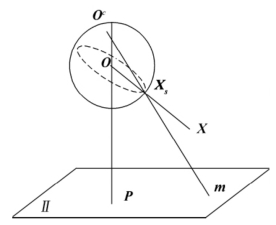
图6－26　空间点的反射折射成像模型

虚拟摄像机的光轴是直线OOc，则直线OOc与像平面Π的交于P＝（u0　v0　1）T为摄像机的主点。Oc到O的距离ξ＝‖O－Oc‖成为镜面参数，不同的镜面参数对应不同类型的反射镜面：当0＜ξ＜1时，对应的反射镜面是双曲面或椭球面；当ξ＝1时，对应的反射镜面是抛物面；当ξ＝0时，对应的反射镜面是平面镜。

全向摄像机的成像过程可表示为

式中，α和［R　T］见（6－1），‖‖指向量范数，ξ指镜面参数。

2）基于标定模板的全向摄像机标定方法

全向摄像机标定仍然是提取三维空间信息必不可少的关键步骤。现已有一系列的标定算法：①基于三维控制点的方法，可以得到较高的标定精度，但需要精度很高的标定精度；②基于二维控制点的方法，使用带有控制点的二维标定块进行标定，能得到较高的标定精度；③基于直线的方法，不需要知道用于标定的空间直线间的相对位置以及直线相对于摄像机的位置关系，仅仅利用直线像的性质来标定反射折射摄像机的内参数；④基于球的方法，不需要已知任何度量信息，只利用球的像来标定摄像机内参数；⑤自标定方法，不需要使用标定块，直接从场景图像出发，但是标定精度不高等。

本小节重点介绍基于平面模板的全向摄像机标定方法，简单阐述基于直线和球的全向摄像机标定方法。如需进一步了解全向摄像机的其他标定方法。

（1）基于平面模板的全向摄像机标定方法　基于模板的标定方法：主要利用具有控制点的二维标定块作为标定物进行摄像机标定。Scaramuzza等假设全向成像过程式（6－7）可以用Taylor展示来表示，其中系数可以通过解一个线性的最小二乘问题得到。在上述假设基础上提出了一种全向摄像机标定方法。然而，Mei和Rives却在标准的全向摄像机成像模型式（6－7）的基础上，提出一种基于平面标定物的全向摄像机标定方法。

邓小明等基于全向成像模型式（6－7）和透视摄像机成像模型式（6－1）之间的变换关系，利用非线性优化方法估计摄像机内外参数。首先，利用反射镜面的投影轮廓线和视角得到摄像机内参数的初始估计；然后，基于全向成像模型和透视摄像机成像模型之间的变换关系得到摄像机外参数的初始估计；最后，通过非线性优化方法得到全向摄像机的内外参数。

通过最小二乘方法拟合反射镜面的投影轮廓线C0。通过C0对摄像机内参数进行初始化。

假设C0的表达式为C0＝［a b d；b c e；d ef］，则摄像机内参数rc，s，u0，v0，fc的初始值为：

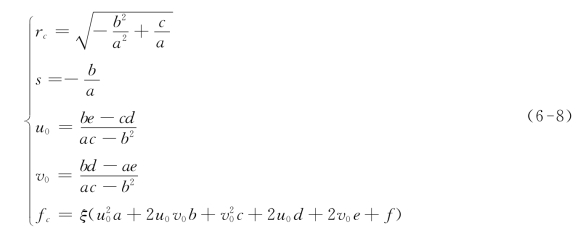
式中，ξ为镜面参数。通常情况下，反射镜面制造商提供的镜面参数是比较准确的，因此这里假设ξ是已知的。

基于平面模板的全向摄像机标定算法如下：

①在全向摄像机下，拍摄k幅平面模板图像，使其覆盖了大部分图像平面，并提取图像点mij，i＝1，2，…k，j＝1，2，…，Nj。

②基于反射镜面的投影轮廓线，利用式（6－8）初始化摄像机内参数。

③基于图像点mij和其空间点坐标Mj，利用DLT（Direct Linear Transformation）算法计算出单应性矩阵Hi，i＝1，2，…k，j＝1，2，…，Nj。

④基于单应性矩阵Hi；初始化外参数矩阵［Ri，Ti］。

⑤通过最小化反投影误差优化估计得到全向摄像机内外参数。

（2）基于已知场景结构信息的全向摄像机标定方法

①基于直线的全向摄像机标定方法：直线在全向摄像机下的像是二次曲线，但在像平面上仅有一小段弧是可见的。因此，传统的二次曲线拟合方法不能准确地拟合直线像的方程。当反射镜面为抛物面时，Barreto and Araujo推导出了直线像需要满足的充要条件，并利用这些条件来限制搜索空间，从而估计直线的像。然而，这种方法很大程度上依赖于直线的数量、可见弧的长度以及提取图像点的数量。鉴于此，段慧仙等研究了直线像上对极点对的性质，并在此基础上提出了一种新的拟合直线像的方法。该方法不仅适用于所有全向摄像机，而且大大提高了直线像的拟合精度。

Barreto和Araujo证明了全向直线像的一些性质具有射影不变性。基于这些性质，通过三条或以上的直线像就能完全标定出摄像机内参数。该标定方法适用于所有全向摄像机，且仅仅需要位于一般位置的k（k≥3）条直线的像。标定算法如下：

步骤1.拟合全向直线的像。

步骤2.对每对二次曲线，计算它们的交点Fij和Bij，根据得到的交点确定相应的直线μij＝Fij∧Bij，i，j＝1，2，3，…，k且i≠j。

步骤3.通过计算μij的交点来估计主点p，i，j＝1，2，3，…，k且i≠j。

步骤4.对每条二次曲线，计算主点p的极线pi，i＝1，2，3，…，k。

步骤5.通过计算极线pi与二次曲线的交点得到圆环点的像ii和ji，i＝1，2，3，…，k。

步骤6.利用ii和ji估计绝对二次曲线的像面，i＝1，2，3，…，k。

步骤7.对进行Cholesky分解来估计摄像机内参数矩阵K。

②基于球的全向摄像机标定方法：由于球的投影轮廓线通常是封闭的二次曲线（椭圆），可以得到很高的拟合精度，从而能得到较高的标定精度。Ying和Hu等提出了一种基于球的标定方法，把直线和球的像统一到一个模型下，并证明了一个球的映射只能提供两个几何不变约束。从这些不变约束中得到了关于反射折射摄像机内参数的约束方程，从而估计出摄像机的内参数。一般来说，两个球的像足以标定摄像机的内参数。由于该方法得到的关于内参数的约束方程是非线性方程，通常情况下求解是很困难的。为此，Ying和Zha提出了一种基于球像的线性全向摄像机标定算法。文中定义了校正的内参数矩阵，绝对二次曲线的校正像（MIAC）以及对偶绝对二次曲线的校正像（DMIAC）。此外，他们发现一个球的像与MIAC相切于两图像点，每一个切点都是由两个相同图像点构成的。在没有任何假设情况下，仅仅需要3个球的像就能够线性地估计出所有的内参数。该方法大大提高了运行速度，且能达到相似的精度。然而，这两种方法仅仅适用于双曲或椭球全向摄像机的内参数标定，对于反射镜面为抛物面的全向摄像机都属于退化情况。

当反射镜面为双曲镜面或椭球面时，基于k个球图像的全向摄像机标定算法如下：

步骤1.从k个球图像上提取像素点，估计球图像方程Ci，i＝2，3，…，k。

步骤2.计算出每个球图像对应的直线方程，i＝2，3，…，k。

步骤3.计算出二次曲线Ci与其对应直线Ici的交点mIi和mJi，i＝2，3，…，k，并估计出绝对二曲线的校正像。

步骤4.如果矩阵为非正定的，则算法终止。

步骤5.如果矩阵为正定的，则利用分解得到校正的内参数矩阵，进而得到内参数矩阵K。

步骤6.通过vci，i＝2，3，…，k，计算出摄像机的外参数矩阵。

当反射镜面为抛物面时，球在全向摄像机下的像是两条二次曲线，Duan和Wu将其定义为一对对极球图像。其中，在像平面上可见的二次曲线称为球的像，在像平面上不可见的二次曲线称为其对极球图像。此外，从球的成像过程可知，球在视球上投影是两个平行圆。因此，球在全向摄像机下的投影可以看成是视球上两个平行圆在一虚拟摄像机下的像，其中虚拟摄像机的光心位于包含两个平行圆的两个平行平面之间。Duan和Wu研究了反射镜面为抛物面的全向摄像机下3对及3对以上对极球图像的性质，并利用这些性质来拟合球图像和对极球图像的方程，进而估计出该全向摄像机的内参数。

当反射镜面为抛物面时，基于k个球图像的全向摄像机标定算法如下：

步骤1.基于k个球图像上提取的像素点估计球图像的方程。

步骤2.在某个视角下，抛物镜面的投影轮廓线在像平面上是可见的。从该投影轮廓线上提取像素点，且用最小二乘方法估计得到投影轮廓线的方程，初始化摄像机内参数。

步骤3.利用初始化的摄像机内参数，基于对极球图像对的性质初始化对极球图像的方程。

步骤4.基于对极球图像对的性质，建立目标函数，并通过最小化目标函数来优化估计对极球图像方程。

步骤5.求出球图像和对极球图像的4个交点。

步骤6.通过两个相离平行圆的性质，从4个交点中找出圆环点的像。

步骤7.由圆环点的像拟合出绝对二次曲线的像。

步骤8.利用Cholesky分解得到全向摄像机内参数矩阵。

3）基于Matlab工具包的全向摄像机标定

基于Matlab工具包OcamCalib＿toolbox（Omni Calibration Toolbox）进行全向摄像机参数标定时，首先制作平面标定模板：黑白棋盘格。平面模板上黑白方格尺寸必须相同，而采集的平面模板图像上方格尺寸不小于20个像素。此外，在摄像机焦距保持不变的前提下，从不同角度、不同位置拍摄多幅平面模板的全向图像。

（1）OcamCalib＿toolbox工具包操作界面　下载OcamCalib＿toolbox工具包。将OmniCalibToolboxImproved.zip文件解压缩到Matlab指定的目录下。拍摄一组平面模板全景图像并进行统一命名，然后将其拷贝到OcamCalib＿toolbox目录中。平面模板全向图像按照基本名在前、数字编号在后的规则进行命名，例如：img＿para＿1，mg＿para＿2，…，img＿para＿N，其中N不大于3位十进制数字。(www.xing528.com)

运行Matlab，将OcamCalib＿toolbox工具包添加到Matlab path环境中。在Matlab命令窗口运行主函数omni＿calib＿gui，则自动弹出如图6－27所示的操作界面。

图6－27　OcamCalib＿toolbox工具包操作界面

如图6－27所示，OcamCalib＿toolbox工具包的操作界面上包含16个功能指令键：

①“Mirror type”：指定反射镜面类型，1or［］表示全向摄像机反射镜面为抛物面，2表示全向摄像机反射镜面为双曲镜面、椭球面或球面等，3表示鱼眼摄像机。

②“Load images”：读入存放在OcamCalib＿toolbox目录中的用于全向摄像机标定的面模板图像。

③“Estimate camera intri.”：利用反射镜面的投影轮廓线估计全向摄像机内参数的初始值。

④“Extract grid corners”：提取平面模板上的角点。

⑤“Draw Grid Estimate”：平面模板角点经过全向摄像机的标定结果被反投影到图像空间。

⑥“Calibration”：基于距离误差的最小化来优化估计全向摄像机参数。

⑦“Rm Calibration”：删除全向摄像机标定结果。

⑧“Analyse error”：对图像空间中的反投影误差进行分析。

⑨“Recomp.corners”：重新提取平面模板上的角点。

⑩“Draw 3D”：绘制全向摄像机坐标系下所有平面模板的3D视场图。

“Plot Pix／Rad errors”：绘制角点到图像中心距离的误差分析图，误差单位为像素。

“Add／Suppress images”：增加或删除图像。

“Show calib results”：显示全向摄像机的标定结果。

“Save”：保存全向摄像机标定结果和角点图像坐标等。

“Load”：读取保存在OcamCalib＿toolbox目录下的标定结果。

“Exit”：退出标定。

（2）全向摄像机参数标定　拍摄的平面模板全向图像可以采用bmp、jpg、tif、pgm等不同的格式进行存储，但用于标定的同一组平面模板全向图像则要求采用相同的格式。本小节将命名为img＿para＿001.pgm～img＿para＿010.pgm的10幅平面模板图像存放在Ocam－Calib＿toolbox目录中。

①指定全向摄像机类型：点击OcamCalib＿toolbox工具包操作界面上“Mirror type”键，在Matlab命令窗口输入1或者空格选定全向摄像机的反射镜面为抛物镜面。

②读取图像：点击OcamCalib＿toolbox工具包操作界面上“Load images”键，在Matlab命令窗口输入图像名称“img＿para＿”及图像格式“p”，则出现如图6－28所示的10幅平面标定模板全向图像缩略图。

图6－28　读取平面模板全向图像的缩略图

③估计全向摄像机内参数的初始值：点击OcamCalib＿toolbox工具包操作界面上“Estimate camera intri.”键，电脑屏幕弹出待提取反射镜面投影轮廓线的图形窗口。利用鼠标点击反射镜面投影轮廓线中心及边缘上一点，则自动拟合出反射镜面的投影轮廓线，如图6－29所示。之后，选择任意一幅平面模板全向图像，如图6－30所示，提取位于一条直线上的至少4个角点来初始估计全向摄像机焦距。

图6－29　反射镜面投影轮廓线

图6－30　提取位于一条直线上的至少4个角点

④提取平面模板全向图像的角点：点击OcamCalib＿toolbox工具包操作界面上“Extract grid corners”键，提取平面模板全向图像上的角点。

当Matlab命令窗口出现“Number（s）of image（s）to process（［］＝all images）＝”时，输入待提取角点的平面模板全向图像编号，并摁“Enter”键。直接摁“Enter”键是指选用缺省值，即提取所有读入的平面模板全向图像角点。

当Matlab命令窗口出现“Window size of corner finder（wintx and winty）”，且出现“wintx（［］＝5）＝”和“winty（［］＝5）＝”时，要求输入角点提取区域窗口的一半宽度m和一半高度n，其中m和n均为单位像素的正整数。直接摁“Enter”键表示选用了缺省值，即为5个像素。通过选定m和n来确定角点提取区域的窗口大小。当输入m和n的值均为8时，窗口大小为17×17像素，电脑屏幕弹出待处理平面模板全向图像的图形窗口，如图6－31所示。

图6－31　待处理平面模板全向图像的图形窗口

当Matlab命令窗口出现“Please press enter after zooming...”时，放大平面模板全向图像，如图6－32所示。之后，通过鼠标顺时针点击平面模板上的4个点来设定选定区域。平面模板坐标系的原点为鼠标点击的第1个角点，如图6－33所示。

图6－32　放大后的平面模板全向图像

图6－33　顺时针提取平面模板全向图像上的4个角点

当Matlab命令窗口出现“Size of each square along the X direction：dx＝；Size of each square along the Y direction：dy＝”时，输入“dx＝42mm”和“dy＝42mm”，则角点提取完成，如图6－34所示。

图6－34　平面模板全向图像角点提取

⑤全向摄像机标定：点击OcamCalib＿toolbox工具包操作界面上“Calibration”键，在Matlab命令窗口显示全向摄像机参数的标定结果，从而完成了全向摄像机参数标定，如图6－35所示。其中，fc为摄像机焦距；cc为摄像机主点坐标；alpha＿c为斜率，默认值为0；kc为畸变参数；err为平面模板上方格的反投影误差的标准方差，单位为像素。

图6－35　全向摄像机参数标定结果

⑥实验误差分析：点击OcamCalib＿toolbox工具包操作界面上“Plot Pix／Rad errors”键，在新的窗口生成角点到图像中心距离的误差分析图，如图6－36所示；点击OcamCalib＿toolbox工具包操作界面上“Analyse error”键，在新的图形窗口显示所有角点的反投影误差坐标，如图6－37所示。

图6－36　点到全向图像中心距离的误差分析图

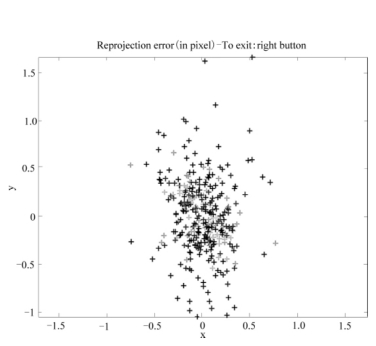
图6－37　角点反投影误差坐标

⑦绘制3D视场图：点击OcamCalib＿toolbox工具包操作界面上“Draw 3D”键，绘制全向摄像机坐标系下所有平面模板的3D视场图，如图6－38所示。

图6－38　全向摄像机坐标系下平面模板3D视场图