多摄像机联动技术实现策略

通常情况下，两三台摄像机即可满足立体视觉领域中的应用需求，其标定过程也比较简单。对此，现已提出了多种经典的多摄像机标定方法。然而，在一些较为复杂的实际应用中，如人体运动捕捉系统，需要顺序摆放8～24台摄像机环绕其运动区域周围。在摄像机数量快速增加的情况下，传统的典型标定方法将不再有效。多摄像机系统为了保证每个摄像机能采集到发生在同一时刻的图像，在硬件方面采用了同步信号发射器，并将支持外同步方式的摄像机通过同步线连接到同步发生器上。与单目摄像机标定方法不同，多摄像机联动标定方法的难点包括：所有摄像机很难同时拍摄到同一标定物；由于所有的摄像机都需要以统一的世界坐标系作为参照，因此需要估计所有摄像机之间的位姿变换矩阵，即外参数矩阵。标定多摄像机内参数时，可以采用单目摄像机标定方法实现每个摄像机的单独标定，也可以把摄像机内外参数统一起来直接求解投影矩阵。目前多摄像机标定方法包括：基于点的多摄像机标定方法、基于一维标定物的多摄像机标定方法、基于二维标定物的多摄像机标定方法、多摄像机自标定方法。

1）摄像机协同标定方法

本小节重点介绍基于二维标定模板的多摄像机协同标定方法。简单阐述基于点、一维标定物的多摄像机标定方法以及多摄像机自标定方法。

（1）基于二维标定物的多摄像机标定方法　假设利用N个摄像机来拍摄位于k个不同位置的平面模板图像。以第1个摄像机坐标系作为世界坐标系，则R1＝I，t1＝0。第i个摄像机下，由摄像机成像过程式（6－1）可以得到空间点M在第i个摄像机下的像mi。Ki为第i个摄像机内参数矩阵，Ri和ti为第i个摄像机相对于第1个摄像机的旋转矩阵和平移向量，为第i个摄像机矩阵。

当平面模板在第j个位置πj时，由摄像机成像过程式（6－1）可以得到空间点M在第i个摄像机下的像。因此，通过单应性变换Hij＝PiQj可以得到平面πj上的空间点M在第i个摄像机下的像，而单应性矩阵在相差一个常数因子的情况下可以通过对应点对｛（x　y）↔（u　v）｝估计得到。其中，Qj为πj的平面矩阵。多摄像机标定模型为：

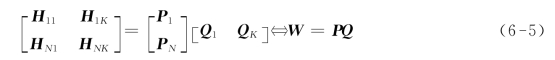
式中，W为测量矩阵（Measurement Matrix）。由式（6－4）可知，测量矩阵的秩为4，从而可以分解为摄像机矩阵和平面矩阵的乘积。因此，若估计出所有单应性矩阵，则可得到摄像机矩阵和平面矩阵。

然而不幸的是，通过匹配对应点只能估计出相差一个常数因子的单应性矩阵，即，其中αij为未知常数因子。则相应的测量矩阵~W的秩不是4，且其不能分解为摄像机矩阵和平面矩阵的乘积。针对此问题，有两种解决方法：一种方法是通过迭代非线性最小化方法搜索一组常数因子αij，使得测量矩阵W的秩为4。然而，此非线性最小化方法计算复杂度高且需要初始化常数因子。另一种方法是基于常数因子的约束条件对测量矩阵~W进行分解，进而估计出摄像机参数矩阵。首先，对测量矩阵~W进行SVD分解；然后，摄像机矩阵的初始值可以通过非线性优化估计得到；最后，通过Levenberg－Marquardt算法优化估计多摄像机参数矩阵。

基于二维平面标定物的多摄像机标定方法证明了模板平面与图像平面之间的单应性矩阵可以分解为摄像机投影矩阵与平面参数矩阵的乘积，并在此基础上构建了测量矩阵。然而，由于在估计每个单应性矩阵时均相差一个常数因子导致测量矩阵不可分解。对此，基于多视角下的单应性矩阵约束估计得到常数因子使得测量矩阵可分解。最后，多摄像机参数的标定精度可以通过非线性优化算法得到提高。

基于二维标定物的多摄像机标定方法，大多数是张正友黑白棋盘格平面标定法的扩展，其中摄像机的标定结果受标定模板的制作精度的影响比较大。然而，标定模板需要被所有摄像机同时观测到是此方法的关键所在，因此，估计摄像机外参数是比较困难的。

为了保证所有摄像机能同时观测到二维标定物，德国学者Theobalt将二维标定模板放置在地面中间，将多摄像机架设到天花板上。固定二维标定模板的一角作为世界坐标系的原点，此时可以利用张正友的基于平面模板的标定方法估计多摄像机的内外参数矩阵。

当所有摄像机无法同时观测到二维标定模板时，需要固定某一个摄像机光心为世界坐标系的原点，基于此求出其他摄像机的外参数矩阵。Toshio通过直接建立多摄像机标定模型，将张正友基于平面标定模板的摄像机标定方法扩展到多摄像机情况下。该方法仅仅需要拍摄平面标定模板在任意不同位置下的几幅图像，因此继承了张正友平面标定方法的灵活性，且其标定精度要优于张正友平面标定方法得到的标定结果。

（2）基于已知景物结构信息的多摄像机标定方法

①基于点的多摄像机标定方法：Tomas Svoboda等人以激光点作为标定物，对3台或3台以上的多摄像机同时进行标定。首先，在分布式环境下将每个摄像机拍摄的点进行匹配；其次，通过对秩为4的测量矩阵（Measurement Matrix）进行分解，进而进行射影重建；然后，基于射影重建来估计摄像机矩阵；最后，通过几何约束实现度量重建。基于此，瑞士联合技术研究院的计算机视觉实验室研发了多摄像机自标定工具箱（Multi－Camera Self－calibration Toolbox）。通过该工具箱进行多摄像机标定时，只需要在待标定空间中晃动标定物，则计算机可完成剩下的全部工作，自动化程度很高。手持标定物进行晃动没有特殊要求，标定物不需要被所有摄像机同时观测到。使用该算法进行多摄像机标定，标定过程比较简单，操作灵活且能得到精度较高的标定结果。然而，该方法还存在有局限性，即为了便于识别与跟踪，需要将标定物放置在相对较暗的标定环境中。

②基于一维标定物的多摄像机标定方法：张正友提出了一种基于一维标定物的多摄像机标定方法。该方法所使用的一维标定物由距离已知的3个空间共线点组成，即将3个小球等距地串接在一根长棍上，如图6－18所示。在进行摄像机标定时，固定长棍的一端，将另一端绕长棍旋转。在不同位置和方向下，每个摄像机拍摄多幅多视角的图像序列；然后，利用每个视角下图像匹配点对的映射关系建立一系列约束方程，初始化摄像机内参数矩阵；最后，通过非线性优化得到多摄像机的内参数矩阵。张正友提出的基于一维标定物的多摄像机标定方法，该方法对标定环境没有特殊要求。然而，该方法存在不足之处在于：无法估计出摄像机的外参数矩阵；标定过程中需要将长棍中的其中两个点绕第3个点转动，操作不太灵活；标定精度也有待提高。此外，张正友还证明了多摄像机的标定精度可以通过增加共线小球的个数来得到提高。

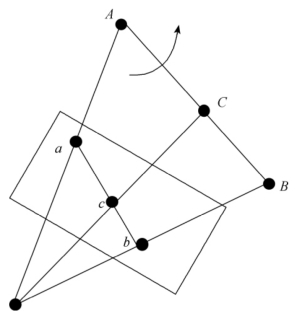
图6－18　一维标定物

Joel等人提出基于一维标定棒的多摄像机标定方法。该方法仅仅要求多个摄像机从不同角度拍摄晃动的标定棒，其中标定棒是由两个距离已知且固定的可见标记点构成。由于该方法并不要求所有摄像机同时拍摄到一维标定棒，因此摄像机之间可以相互对立放置。基于一维标定棒的多摄像机标定方法包括一个新的自动初始化摄像机参数过程和一个光束平差法优化摄像机参数过程。其中，光束平差法优化过程是对每个视图下的特征点基于捆绑调整法（Bundle Adjustment）最小化投影误差得到优化的摄像机参数。具体标定方法为：首先，在空间中随机晃动带有标记点的一维标定棒，并由多个摄像机同时拍摄；其次，对每个视图进行自动特征提取，并计算每个标记点在三维空间中的位置；之后，根据标记点的像素坐标和两个标记点之间的距离初始化摄像机内外参数；最后，基于初始化的摄像机内参数，利用捆绑调整法最小化投影误差来优化摄像机内外参数。针对由8个摄像机构成的视觉系统，基于一维标定棒的多摄像机标定方法较基于图表（Chart－Based）的标定方法具有更高的时效性。

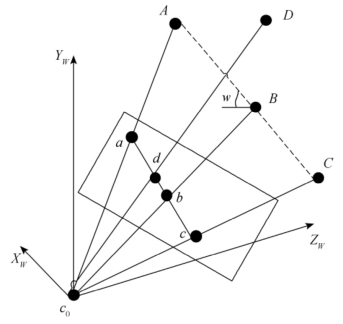
图6－19　基于消失点的标定物

③基于消失点约束的多摄像机标定方法：基于一维标定物的多摄像机标定方法存在精度低、稳定性差、参数求解冗余等问题，对此，张超等人提出了一种基于消失点约束的多摄像机标定方法，所使用的标定物如图6－19所示。标定物由三个共线特征点A，B，C和一个非共线特征点D构成，其中特征点D到共线特征点的垂点位于特征点A，B之间。首先，由于摄像机镜头畸变会导致理论上推导出的标定模型产生相应的误差。因此，为了避免摄像机镜头畸变对成像造成的影响，通过欧式空间位置约束的几何特性对摄像机径向畸变参数进行求解。进一步地为了提高摄像机标定精度，通过一维标定物上的特征点约束以及摄像机的射影不变性来排除外点的干扰。之后，基于一维标定物上特征点所在的直线与消失点的反向射线的平行性以及空间消失点之间夹角的一致性对多摄像机的参数进行估计。最后，利用捆绑调整法对摄像机参数整体进行非线性优化，以减少加性噪声对系统的影响。基于消失点约束的多摄像机标定方法通过采用多点在欧式空间中的位置约束关系对摄像机镜头的径向畸变进行校正。基于校正后的图像点，利用消失点夹角的一致性、恒定性以及其反向射线的平行性对摄像机的内外参数进行线性求解，并通过捆绑调整法对摄像机参数整体进行非线性优化。通过大量实验验证，基于消失点约束的多摄像机标定方法具有较高的标定结果，且随着噪声的增加，标定结果也表现出了一定的抗噪性和鲁棒性。

（3）多摄像机的自标定方法　由固定在同一平台上的两台摄像机构成的摄像机对（Stereo Rig）称之为双目立体摄像机。双目立体摄像机之间的相对位姿是保持不变的。为了实现所拍摄的景物中能够存在大部分重叠区域，双目立体摄像机之间的基线一般都比较短。该双目立体摄像机被广泛应用于三维重建、视频监控、机器人导航等领域。

双目立体摄像机的自标定原理与单目摄像机的自标定原理在本质上是相同的，但也存在其独特性。例如：相对于弹幕摄像机，双目立体摄像机的匹配和标定过程更为简单。现已提出了多种双目立体摄像机的自标定方法。特别是当斜率为0且摄像机主点已知时，通过最小化图像序列上所有点到对应极线的距离之和可以估计摄像机内参数。

2）基于Matlab工具包的双目立体摄像机标定

通常情况下，可以通过自动加载安装MCRInstaller－64.exe，并将安装目录“＼runtime＼win32”路径添加到电脑的环境变量中。如果不能自动加载，也可以手动安装。手动安装方法是：右击“我的电脑”→“属性”→“高级”→“环境变量”→“添加”。注：当安装过程中弹出Microsoft.NETFramework时，可以不用安装。

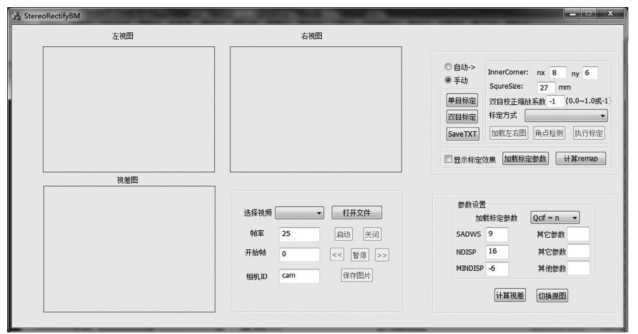
其次，基于Matlab工具包toolbox＿calib的双目立体摄像机标定一共分为三个步骤：①同时截取并保存左右各10～20组平面模板图像；②按照图6－20所示界面右上角手动标定下单目-双目－save－计算remap的顺序进行标定和保存；③测试标定参数是否合理。

(www.xing528.com)

图6－20　双目立体摄像机标定界面

基于Matlab工具包toolbox＿calib的双目立体摄像机标定步骤如下：

（1）从二进制视频中截取并保存平面模板图像　视频存储格式分为左右分开和合并两种，如图6－21所示。首先，选择存储格式后分别打开文件；其次，利用所拍摄视频的摄像机名字为该段视频命名，避免不同摄像机的参数产生混淆；最后，启动播放视频，点击保存不同位置下的平面模板图像，该图像将自动保存在以摄像机名字命名的文件夹下。

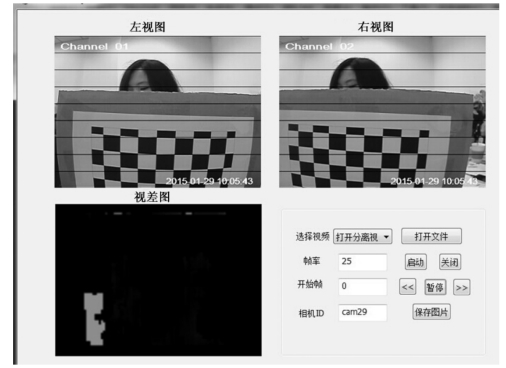
图6－21　从二进制视频中截取并保存黑白棋盘格图像

（2）双目立体摄像机标定　目前，可以通过Opencv和Matlab两种工具包实现双目立体摄像机的参数标定。其中，基于Opencv工具包可以自动完成摄像机参数标定，即仅仅需要读取待标定图像。然而，自动检测的图像角点精度很低。因此，如果需要高精度的双目立体摄像机标定结果，则建议采用基于Matlab工具包toolbox＿calib的手动标定。

基于Matlab工具包toolbox＿calib的双目立体摄像机标定分为单目标定、双目标定两个步骤。

首先，分别命名左右摄像机采集的平面模板图像：左摄像机采集的图像命名为left1～leftN；右摄像机采集的图像命名为right1～rightN。然后点击“单目标定”，按照6.1.1节所述方法分别对左右摄像机内外参数进行标定并保存标定结果。左右摄像机内参数的标定结果分别保存为“Calib＿Results＿left.mat”和“Calib＿Results＿right.mat”。

其次，在Matlab命令窗口运行主函数stereo＿gui指令，则电脑屏幕将出现图6－22所示界面。

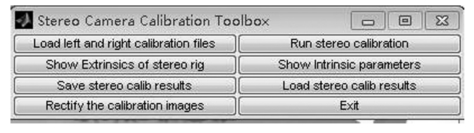
图6－22　toolbox＿calib工具包双目立体标定操作界面

①点击toolbox＿calib工具包双目立体标定操作界面上“Load left and right calibration files”键，读取左右摄像机的标定结果，并初步估计左摄像机相对于右摄像机的位姿。

在Matlab命令窗口输入左右摄像机标定结果文件名：“Calib＿Results＿left.mat”和“Calib＿Results＿right.mat”，则得到如图6－23所示的双目立体摄像机初始标定结果。

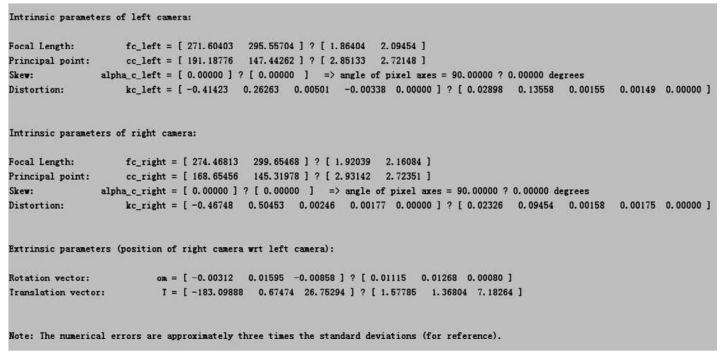
图6－23　双目立体摄像机初始标定结果

②点击toolbox＿calib工具包双目立体标定操作界面上“Run stereo calibration”键，对双目立体摄像机的内参数以及左摄像机相对于右摄像机的位姿进行优化，得到如图6－24优化后的双目立体摄像机标定结果。

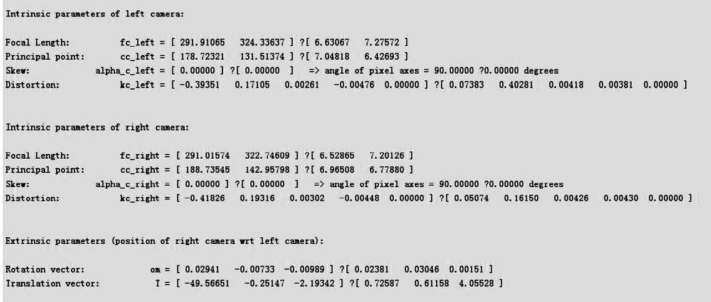
图6－24　优化后的双目立体摄像机标定结果

③点击toolbox＿calib工具包双目立体标定操作界面上“Show Extrinsics of stereo rig”键，显示平面模板在摄像机坐标系下的位姿。

④点击toolbox＿calib工具包双目立体标定操作界面上“Show Intrinsic parameters”键，在Matlab命令窗口显示优化后的双目立体摄像机标定结果。

⑤点击toolbox＿calib工具包双目立体标定操作界面上“Save stereo calib results”键，将双目立体摄像机标定结果以Calib＿Results＿stereo.mat文件格式保存在toolbox＿calib目录下。

⑥点击toolbox＿calib工具包双目立体标定操作界面上“Load stereo calib results”键，读取保存在toolbox＿calib目录下的双目立体摄像机标定结果文件Calib＿Results＿stereo.mat。

⑦点击toolbox＿calib工具包双目立体标定操作界面上“Rectify the calibration images”键，根据估计的畸变参数对左右摄像机拍摄的平面模板图像作畸变矫正处理，并将畸变矫正结果保存在toolbox＿calib目录下，其文件名为将“＿rectified”插入到原始图像文件名的基本名和编号之间。

⑧点击toolbox＿calib工具包双目立体标定操作界面上“Exit”键，退出双目立体摄像机标定。

（3）双目立体匹配演示　通过BM立体匹配方法演示基于双目立体摄像机标定结果下的图像匹配效果，如图6－25所示。

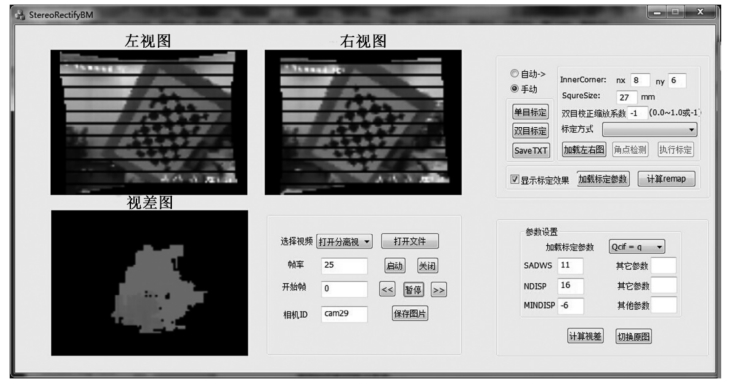
图6－25　双目立体匹配结果演示图