传统摄像机标定方法详解

传统的摄像机标定方法包括张正友的平面标定方法、直接线性变换（DLT变换）方法、RAC方法、孟晓桥和胡占义的圆标定方法、吴毅红等的平行圆标定方法等。其特点是以已知的景物空间结构为基础标定模板。该方法的优点在于不仅标定精度高且可以适用于所有的摄像机成像模型；但也有不足之处：标定过程复杂；需要精度很高的已知景物空间结构信息；在实际应用过程中，由于标定模板特有的性质使其在很多情况下都无法用于恢复摄像机的内外参数。

1）基于标定模板的摄像机标定方法

本小节重点介绍张正友的基于平面模板的摄像机标定方法，简单阐述直接线性变换（DLT变换）、RAC方法、孟晓桥和胡占义的圆标定方法、吴毅红等的平行圆标定方法等。

（1）基于平面模板的摄像机标定方法　基于二维平面模板的摄像机标定方法，只需要通过移动平面模板或摄像机从不同（至少2个）方位拍摄平面模板，不需要知道平面模板或摄像机移动的具体方向或位置信息，而且平面模板制作简单。张正友提出了一种基于黑白棋盘格的摄像机标定算法，成像模型见图6－2。该方法介于传统标定方法和自标定方法之间，既避免了传统方法设备要求高，操作繁琐等缺点，同时又比自标定方法精度高，从而符合办公、家庭使用的桌面视觉系统（DVS）的标定要求。首先，假设世界坐标系的Zw＝0平面位于黑白棋盘格所在的平面，确定黑白棋盘格中每个小方格的角点在世界坐标系下的坐标；其次，从3个或3个以上的角度拍摄黑白棋盘格图像，并提取图像中每个角点的像素坐标；然后，基于提取得到的像素坐标与其对应的空间坐标来估计单应性矩阵；最后，通过分解估计出的单应性矩阵来恢复摄像机的内外参数。

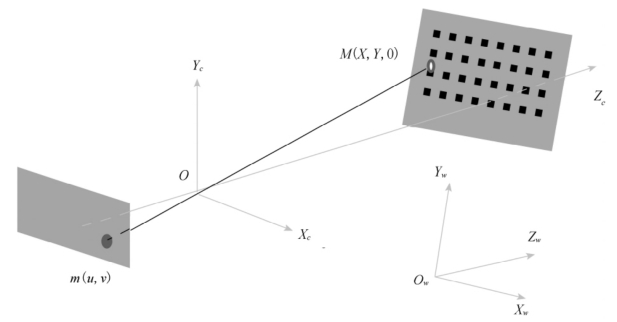
图6－2　基于平面模板的成像模型

假设世界坐标系的Zw＝0平面位于黑白棋盘格所在的平面，则单应性矩阵H描述了空间中Zw＝0平面上三维点与摄像机平面二维图像点之间的关系。由摄像机成像过程式（6－1）可知，H＝［h1 h2 h3］＝σK［r1 r2 T］，其中K为摄像机的内参数矩阵，R＝（r1，r2，r3）和T分别是摄像机坐标系相对于世界坐标系的旋转矩阵和平移向量。因为摄像机图像平面中点的坐标可以通过图像处理的方式（Harris角点，再基于梯度搜索的方式精确控制点位置）获取，而空间中平面三维点可以通过预先做好的黑白棋盘格获取。因此，每幅平面模板的图像都可以计算出一个单应性矩阵H。

由旋转矩阵和单应性矩阵的性质可以得到关于摄像机内参数的两个约束方程。因此，通过一幅黑白棋盘格图像即可以得到关于摄像机内参数的两个基本约束。众所周知，摄像机有5个未知内参数，因此拍摄大于等于3幅黑白棋盘格图像，即可线性地唯一求解出摄像机内参数矩阵K。

算法步骤：

步骤1.打印一张黑白棋盘格模板并贴在一个平面上。

步骤2.通过移动摄像机或平面模板，获得不同角度的k（k≥3）张平面模板图像。

步骤3.在黑白棋盘格图像上提取特征点。

步骤4.根据单应性矩阵的性质及其对内参数矩阵的基本约束（式（6－2）），估计出摄像机的内外参数矩阵。

黑白棋盘格平面模板如图6－3所示。

图6－3　平面标定模板

张正友提出的基于黑白棋盘格平面模板的标定方法需要确定棋盘格平面模板上点阵的物理坐标以及图像和模板之间点的匹配，这不便于不熟悉计算机视觉的用户使用。此外，该方法对摄像机的要求相对较高，不允许摄像机有较大的径向畸变，否则得到的参数存在很大的差异，但是这一缺陷可通过畸变校正解决。

（2）基于已知景物空间结构信息的摄像机标定方法

①直接线性变换方法（DLT变换）：Abdal－Aziz和Karara提出了直接线性变换摄像机标定的方法，从摄影测量学的角度深入地研究了摄像机图像和物理环境物体之间的关系，构建了摄像机成像的几何线性模型。通过对线性方程的求解可以完全估计出摄像机成像几何线性模型的参数。

由摄像机成像过程式（6－1），可以得到空间点与其对应图像点之间的关系，由两个方程组成。从而，当已知N个空间点和其对应的图像上的点时，则可以得到一个关于摄像机参数的含有2N个方程的方程组。因此，通过最小化带有约束条件的目标函数得到最优解，进而标定出摄像机内外参数。其中，目标函数由关于摄像机参数的2N个方程构成，而约束条件不具有旋转和平移的不变性。

②RAC摄像机标定方法：Tsai提出的基于径向一致性约束（RAC）的标定方法是计算机视觉摄像机标定方面的一项重要工作，该方法的核心是利用径向一致约束来求解除tz（摄像机光轴方向的平移）外的其他摄像机外参数，然后再求解摄像机的其他参数。基于RAC方法的最大好处是它所使用的大部分方程是线性方程，从而降低了参数求解的复杂性，因此其定标过程快捷、准确。

算法步骤：

步骤1.通过径向一致约束来估计世界坐标系与摄像机坐标系之间的旋转矩阵R，平移向量T的前两个元素t1，t2和位率rc。

根据摄像机成像过程式（6－1）和径向一致约束，由至少7组对应点，可以求得旋转矩阵、平移向量、位率相关的一组解（r1，r2，r3，t1，rcr4，rcr5，rcr6，rct2）。进一步，基于旋转矩阵的性质即可求出（r7，r8，r9）和rc，从而t2也可以被解出。

步骤2.求解有效焦距fc，平移向量T的第三个元素t3和畸变参数k。

令k＝0作为初始值，根据径向一致约束以及步骤1中求出的R，t1，t2和位率rc，则可以解出焦距fc，t3。进一步地，将求出的fc，t3以及k＝0作为初始值进行线性优化即可估计出焦距fc，平移向量t3和畸变参数k的真实值。

③基于平面圆的摄像机标定方法：张正友提出的基于平面模板的标定方法，需要确定棋盘格平面模板上点阵的物理坐标以及图像和模板之间点的匹配，当拍摄图像和选取的点较多时，图像和模板之间匹配关系的确定将成为一种极大的负担，给使用者带来了不便。针对这一不足之处，孟晓乔和胡占义提出了一种基于圆环点的摄像机标定方法。该方法仅仅需要摄像机在3个（或3个以上）不同方位拍摄一个含有若干条直径的圆的图像，即可线性求解出所有摄像机内参数。

不同于黑白棋盘格平面模板，孟晓乔和胡占义使用的新的标定模板如图6－4所示。

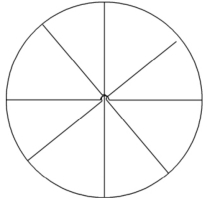
图6－4　基于圆的标定模板

考虑圆所在平面模板的无穷远直线上的两个特殊点：一对圆环点。不难证明，圆环点位于绝对二次曲线上，则其对应的图像点位于绝对二次曲线的像上。因此，根据射影不变性计算出每幅标定模板图像上圆环点像的坐标，可以得到关于内参数矩阵的6个（或6个以上）方程，即可线性求解出所有摄像机内参数。

算法步骤：

步骤1.打印一个圆及通过圆心的若干条直线（如图6－4所示），并贴在一个平面上。

步骤2.为避免退化情形，需要改变摄像机与模板的相对位置，使得摄像机与模板平面之间的相对姿态不同且模板平面与图像平面不平行。满足此条件下，获得不同姿态下的k（k≥3）张平面模板图像。

步骤3.采用随机Hough变换提取直线，基于代数距离的最小二乘法来检测圆像，估计出圆像和直线的方程。

步骤4.如图6－4所示，通过直线束Li，i＝1，2，…，N，在最小二乘意义下拟合出隐消线（无穷远直线的像）的方程。

步骤5.联立圆像和隐消线方程计算出圆环点的像坐标。

步骤6.得到k（k≥3）幅图像上的圆环点像的坐标，从而线性求解出摄像机的内参数。

由此可见，孟晓桥和胡占义提出的基于平面圆的标定方法与张正友提出的基于平面模板的标定方法过程相似，但所用的模版不同。基于平面圆的标定方法不需要确定模板和图像点之间的匹配关系，也不需要知道模板上的任何物理度量，完全摆脱了人工干预。整个标定过程十分简单且能够实现全自动标定。

④基于平行圆的摄像机标定方法：Wu等人定义了两个共面圆的相伴直线，并给出了任何两个共面圆与其相伴直线的位置关系。此外，他们还证明了没有实交点的两个共面圆与其相伴直线的位置关系满足准仿射不变性。平行圆是指同一个平面上的两个圆或两个平行平面上的两个圆。因此，根据两个共面圆与其相伴直线的位置关系，Wu等人提出了基于平行圆的摄像机标定方法。该方法是从平行圆的最小个数出发，利用摄像机成像的准仿射不变性，分析所有可能情况的圆环点的计算方法，计算图像上二次曲线的交点，从而得到圆环点的像，进而估计出摄像机的内参数矩阵。与基于平面圆的标定方法相比，计算圆环点图像简单，只需要从拟合的二次曲线出发，不需要各个视图之间的任何匹配，不需要计算圆心。这种方法应用场合广泛，不仅仅限于平面的情形，可应用基于转盘的重构。

算法步骤：

步骤1.从k个不同视角下的圆像上，拟合两个平行圆的像C＋i和C－i，i＝2，3，…，k。

步骤2.求出两条二次曲线C＋i和C－i的四个交点，i＝2，3，…，k。

步骤3.根据平行圆与其相伴直线的位置关系，从C＋i和C－i的四个交点中找出圆环点的像，i＝2，3，…，k。

步骤4.由圆环点的像拟合出绝对二次曲线的像ῶ＝K－T K－1。

步骤5.利用Cholesky分解得到内参数矩阵K。

2）基于Matlab工具包的摄像机标定

基于Matlab的摄像机标定工具包toolbox＿calib，按照图6－5所示的流程实现摄像机的内外参数估计。

图6－5　基于Matlab工具包的摄像机标定流程

基于Matlab工具包toolbox＿calib进行摄像机内外参数标定时，首先需要制作平面标定模板：黑白棋盘格。平面模板上黑白方格尺寸必须相同，而采集的平面模板图像上方格尺寸大小不小于20个像素。此外，在摄像机焦距保持不变的前提下采集平面模板图像，需要在不同角度、不同位置采集多幅图像。

（1）toolbox＿calib工具包操作界面　下载toolbox＿calib工具包，解压缩工具包中toolbox＿calib.zip文件，之后将其拷贝到Matlab指定的目录下。

采集一组平面模板图像并进行统一命名，然后将其拷贝到toolbox＿calib目录中。平面模板图像的命名规则为基本名在前，数字编号在后，例如：left1、left2、…、leftN，其中N不大于3位十进制数字。

运行Matlab，将toolbox＿calib工具包添加到Matlab path环境中。在Matlab命令窗口运行主函数calib＿gui指令来调用标定函数calib＿gui.m，则弹出以下界面：

图6－6　toolbox＿calib工具包模式菜单

如图6－6所示，有两种模式“Standard”和“Memory efficient”可供选择。“Standard”是指将目录中的所有图像一次性读入内存中，所需内存比较大；而“Memory efficient”是指根据需要每次将目录中一幅图像读入内存中，所需内存比较小。在选择模式之后，电脑屏幕会弹出工具包操作界面，从而可以使用toolbox＿calib工具包完成摄像机标定。(www.xing528.com)

在图6－6中选择“Standard”模式后，电脑屏幕弹出如图6－7所示的操作界面。

图6－7　toolbox＿calib工具包操作界面

如图6－7所示，toolbox＿calib工具包操作界面上具有16个功能指令键：

（a）“Image names”：是指定读取图像的基本名（Basename）和图像存储格式；

（b）“Read images”：是按照指定的基本名和格式将相应的图像读入内存中；

（c）“Extract grid corners”：是指提取平面模板上的角点；

（d）“Calibration”：利用张正友的基于平面模板的方法标定摄像机内参数；

（e）“Show Extrinsic”：通过图形的方式显示摄像机与标定板之间的关系；

（f）“Reproject on images”：按照平面模板的笛卡尔空间坐标，根据摄像机的内外参数，将平面模板角点反投影到图像空间；

（g）“Analyse error”：在图像空间进行误差分析；

（h）“Recomp.corners”：重新提取平面模板的角点；

（i）“Add／Suppress images”：增加或删除图像；

（j）“Save”：将摄像机内外参数标定结果保存为m文件：Calib＿results.m，并存放在toolbox＿calib目录中；

（k）“Load”：读入存放在toolbox＿calib目录中的标定结果文件Calib＿results.m；

（l）“Exit”：退出标定；

（m）“Comp.Extrinsic”：估计摄像机外参数；

（n）“Undistort image”：对图像畸变进行校正并保存校正后的图像；

（o）“Export calib data”：将每幅平面模板图像的角点分别以平面模板上的平面坐标和图像中的图像坐标保存为两个tex文件；

（p）“Show calib results”：显示标定结果。

（2）摄像机内外参数标定　采集的平面模板图像可以采用bmp、jpg、tif等不同的格式进行存储，但用于标定的同一组平面模板图像需要采用相同的格式。本小节将命名为left1.bmp～left9.bmp的9幅平面模板图像存放在toolbox＿calib目录中。

①读取图像：点击toolbox＿calib工具包操作界面上“Image names”键来调用函数ima＿read＿calib.m和check＿active＿images.m。在Matlab命令窗口输入图像名称“left”及图像格式“b”，则出现如图6－8所示内容以完成图像读取，同时显示9幅平面模板标定图像缩略图，如图6－9所示。

图6－8　输入图像名称及图像格式

图6－9　读取平面模板图像的缩略图

②提取图像中的角点：点击toolbox＿calib工具包操作界面上“Extract grid corners”键来调用函数click＿calib.m和click＿ima＿calib.m。

当Matlab命令窗口出现“Number（s）of image（s）to process（［］＝all images）＝”时，输入需要进行角点提取的平面模板图像的编号并摁“Enter”键。直接摁“Enter”键表示选用缺省值，则对读取的所有平面模板图像提取角点。

当Matlab命令窗口出现“Window size of corner finder（wintx and winty）”时，分别在“wintx（［］＝3）＝”和“winty（［］＝3）＝”输入角点提取区域窗口的一半宽度m和一半高度n，其中m和n均为单位为像素的正整数。直接摁“Enter”键表示选用缺省值，为3个像素。选定m和n则能得到角点提取区域的窗口大小。当m和n均为缺省值时，窗口大小为7×7像素。

当Matlab命令窗口出现“Do you want to use the automatic square counting mechanism（0＝［］＝default）or do you always want to enter the number of squares manually（1，other）？”时，选择缺省值0表示工具包自动计算平面模板在选定区域内方格的行数和列数；而选择1则表示输入通过人工计算得到的平面模板在选定区域内方格的行数和列数。

当Matlab命令窗口出现“Processing image 1...Using（wintx，winty）＝（3，3）－Window size＝7×7Click on the four extreme corners of the rectangular complete pattern（the first clicked corner is the origin）...”时，电脑屏幕弹出待处理平面模板图像的图形窗口，如图6－10所示。然后，利用鼠标点击4个点来设定平面模板上的选定区域。点击的第1个角点作为平面模板坐标系的原点，顺时针点击4个角点形成四边形。

图6－10　待处理平面模板图像的图形窗口

图6－11　提取角点的标定图像

当Matlab命令窗口出现“Size of each square along the X direction：dX＝100mm Size of each square along the Y direction：dY＝100mm”时，分别输入平面模板上方格的长度和宽度，单位mm，其缺省值均为100mm。

当Matlab命令窗口出现“Need of an initial guess for distortion？（［］＝no，other＝yes）”时，缺省值为no，表示不输入畸变参数初始值，而选择yes则表示需要输入畸变参数初始值。

按照以上角点提取步骤依次对9幅图像进行相同的操作，所有参数均选择缺省值时，可以得到9张类似于图6－11所示的带有角点的平面模板图像。从图6－10可以看出，每个角点提取的区域窗口均包含了角点，且角点提取结果的十字标记位置与角点位置吻合，表明平面模板上角点提取准确。

③标定摄像机内参数：点击toolbox＿calib工具包操作界面上“Calibration”键实现摄像机内参数标定。

首先，对摄像机内参数进行初始化，即将图像中心坐标作为摄像机主点的初始估计值，其他摄像机内参数则由平面模板上方格的消失点估计得到，而畸变参数初始值为0。点击“Calibration”键后，在Matlab命令窗口显示摄像机初始的标定结果和优化后的标定结果，如图6－11所示。采用是L－M梯度下降法对摄像机内参数进行优化。此外，优化后的标定结果中还给出了各个参数的不确定性，即3倍的标准方差。如图6－12所示，fc为摄像机焦距；cc为摄像机主点坐标；alpha＿c为斜率，对应于图像坐标v的摄像机实际y轴与理想y轴之间的夹角，单位为弧度，默认值为0；kc为畸变参数；err为平面模板上方格反投影到图像空间的误差的标准方差，单位为像素。在优化后的标定结果中，不确定性的数值越小，则说明标定精度越高；反之，如果不确定性数值与结果值相比所占比例较大，则需要对摄像机内参数进行重新标定。

图6－12　摄像机内参数标定结果

④显示平面模板与摄像机之间的关系：点击toolbox＿calib工具包操作界面上“Show Extrinsic”键在新的图形窗口中显示平面模板与摄像机之间的关系，如图6－13所示。

图6－13　摄像机与平面模板之间的关系

图6－14　角点反投影到图像空间中的坐标误差

⑤实验误差分析：点击toolbox＿calib工具包操作界面上“Analyse error”键在新的图形窗口中显示所有角点反投影到图像空间中的坐标误差，如图6－14所示。在图6－14中所示的图形窗口，利用鼠标十字标尺点击选择角点，则可在Matlab命令窗口显示该角点的所属图像、索引号、图像坐标、反投影后的图像坐标、角点提取的区域窗口大小等信息。

⑥反投影到图像空间：点击toolbox＿calib工具包操作界面上“Project on image”键，在Matlab命令窗口中出现“Number（s）of image（s）to show（［］＝all images）＝”时，输入需要进行反投影的平面模板图像的编号并摁“Enter”键。直接摁“Enter”键则表示对所有用于标定的平面模板图像均进行反投影处理。选择对图像left1.bmp进行反投影处理，则在新的图形窗口显示处理结果，如图6－15所示。同时在Matlab命令窗口输出平面模板上所有角点反投影误差的标定方差。如图6－15所示，“＋”为平面模板上角点的图像坐标位置，“o”为角点反投影到图像空间的图像坐标位置。

图6－15　平面模板图像left1的角点反投影结果

⑦矫正图像畸变：点击toolbox＿calib工具包操作界面上“Undistort image”键，则按照标定得到的畸变参数对所有平面模板图像进行畸变矫正处理，得到矫正后的图像并将其保存在toolbox＿calib目录下。图6－16所示为left1平面模板的原始图像和畸变矫正后的图像，其中左图为原始图像，右图为畸变矫正后的图像。

图6－16　平面模板图像left1.bmp的原始图像和畸变矫正后的图像

⑧标定摄像机外参数：点击toolbox＿calib工具包操作界面上“Comp.Extrinsic”键，在Matlab命令窗口输入平面模板图像名称“left1”和格式“b”，通过提取角点可估计出平面模板相对于摄像机的外参数，从而完成摄像机外参数标定。如图6－17所示为摄像机外参数标定结果。其中，Tc＿ext为平面模板坐标系原点相对于摄像机坐标系的平移向量，单位为mm；omc＿ext为对应于平面模板坐标系与摄像机坐标系之间姿态矩阵的Rodrigues旋转向量；Rc＿ext为平面模板坐标系与摄像机坐标系之间的旋转矩阵；err为角点到图像空间的反投影误差的标准差。

图6－17　摄像机外参数标定结果