点跟踪和统计法：目标跟踪的两种常用方法

点跟踪方法中要求用点表示检测目标并建立它们间的对应关系。这种对应关系是一个相当复杂的问题，尤其是目标出现遮挡、误检、进入和消失时。总之，点对应关系的方法可以分为两大类：判定法和统计法。判定法采用量化动作启发式法约束点对应关系问题，而统计法则使用概率手段考察目标并把不确定性引入到点关系的模型中。

1）判定法

这类方法首先使用一系列约束定义了将t-1帧中目标和t帧中某一目标对应的成本。最小化对应关系的成本其实是一个组合优化问题，即通过使用贪婪算法计算出一一对应关系，如图2－6所示。一般地，通常有以下几种定义对应关系成本的约束。

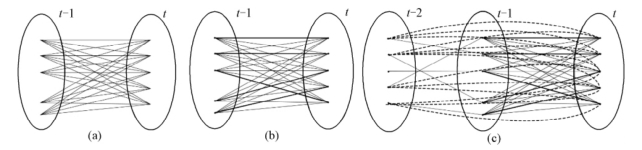
图2－6　点匹配

（1）假设目标的位置在相邻两帧间不会发生显著变化，如图2－7（a）所示。

（2）最大速率定义了目标速度的上限，从而保证了目标在下一帧中的位置不会超过某个半径范围，如图2－7（b）所示。

（3）平滑运动假定目标的运动方向和运动速度不会发生剧烈变化，如图2－7（c）所示。

（4）普遍性运动限制了在小范围内目标的运动速率大致相同。这个约束适用于用多点表示的目标，如图2－7（d）所示。

（5）刚性约束假定物体在三维空间内是刚性的，因此物体上任意两点间的距离是不变的，如图2－7（e）所示。

（6）近似一致性约束是近似性和速率平滑的组合。

然而我们应该注意到，这些约束并不是判定法独有的，它们也可以用在统计法中。

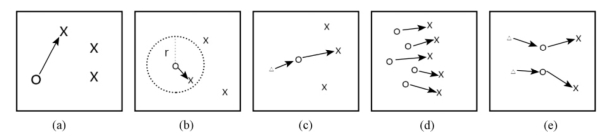
图2－7　运动约束条件差异

很多学者基于近似和刚体约束用贪婪法解决了点对应的问题。这种算法考虑了两个连续帧且基于最近领域标准进行初始化。反复地交换对应关系求得成本最小化。这个算法也可以从后向前取连续帧进行分析。然而，这种方法无法处理目标遮挡、进入和消失等问题。后来，学者们改良了这一方法，先建立检测点的对应关系，然后增加了很多假设点以延伸跟踪消失的目标。

有些研究者基于近似一致性约束提出了贪婪算法实现目标跟踪。算法首先计算最开始的两帧光流得到初始的点对应关系。然而这种方法依然不能处理跟踪过程中目标的出现和消失。如果被检测的点数量减少，可能出现了遮挡或者误检。遮挡可以通过在当前帧中建立检测目标的对应关系；对于剩下的目标，可以基于固定的速度预测它们的位置。此外，也可以使用背景差方法检测目标，检查图像中特定区域以便处理目标数量改变，在计算对应关系之前检测目标的出现和消失。共同动作约束条件对于同一目标上点的连续跟踪具有很强的约束，然而，它不适用于不同运动方向上的多个目标上的点。这一算法初始化时用Two－pass算法获取连通区域，接着使用匈牙利算法最小化连续两帧的匹配成本。这个算法可以解决遮挡和误检的问题，但是不能解决目标出现和消失的问题。

研究者也提出了基于多帧信息的跟踪算法。这个算法可以确保速度和位置的时序一致性。他们把点对应关系问题转换为图论中的理论问题，即多帧的对应关系就是寻找最佳路径Pi＝｛x0，x1，…，xk｝（上标表示帧号）。对于遮挡和误检，这个路径将包含对应帧中的错误的位置。对于k帧中的每个目标点，分裂成两个子节点（“＋”和“－”），有向边连接这两个节点，方向从“＋”到“－”构造一个二分有向图；再通过贪婪法计算匹配关系；处理遮挡问题时，他们使用多帧中点对应的窗口处理。

2）统计法

统计法也是目标跟踪中的常用方法。视频传感器采集到的测量数据总是包含噪声，而且目标的运动可能会受到随机扰动，比如运动的车辆。统计法通过考虑不确定性等因素来实现目标的跟踪。统计法使用状态空间方法来模拟对象的属性，如位置、速度和加速度。测量数据通常包括目标在检测获得的图像中所处的位置。下面，我们将简要介绍在点跟踪的背景下的状态估计方法，这些方法可用于估计任何时变系统的状态，例如，广泛用于轮廓跟踪、活动识别、行为识别、目标识别和运动结构。(www.xing528.com)

通过递归贝叶斯滤波器分两步计算获得理论的最优解。第一步是预测，使用动态方程和已经计算得到的状态概率密度函数获得当前状态下的概率密度先验；第二步是校正，使用最大似然估计函数法计算后验概率。单目标跟踪仅仅需要目标状态的测量数据，而多目标跟踪，测量数据需要对目标状态进行关联。

（1）单一目标的状态估计　如果ft和ht是线性的且初始状态值和噪声服从高斯分布，卡尔曼滤波方法给出了最优状态估计。然而一般情况下，目标的状态未必服从高斯分布，可以使用粒子滤波器对状态进行估计。如果线性系统的状态服从高斯分布，卡尔曼滤波器是用来估计线性系统的状态。该滤波器包含预测和校正两个步骤。预测步骤使用状态模型来预测变量的新状态。校正环节中使用当前的观测值Zt来更新对象的状态值，更新后的状态Xt仍然服从高斯分布。

如果ft和ht是非线性的，可用泰勒级数线性化来得到扩展的卡尔曼滤波器。类似于卡尔曼滤波，扩展卡尔曼滤波器依然需要假设状态服从高斯分布。

卡尔曼滤波器已被广泛应用于视觉跟踪领域。在三维立体视角的目标跟踪中，可以利用卡尔曼滤波器预测目标在x－z维平面上的位置和速度或利用扩展卡尔曼滤波器从二维运动轨迹中估计目标的三维轨迹。

卡尔曼滤波器的一个局限就是假设状态变量符合正态分布。因此，卡尔曼滤波器对不遵循高斯分布的状态变量的估计不足。通过使用粒子滤波可以克服这个限制。

在粒子滤波中，除了跟踪最好的粒子外，算法需要再采样以便淘汰掉权重过低的样本。后验密度不用必须服从高斯分布，粒子滤波器近来受到计算机视觉领域的广泛关注，特别应用在目标检测和跟踪中。

卡尔曼滤波和粒子滤波方法都假设每一个时间段进行一次度量，即估算单目标的状态。跟踪多目标需要对数据关联性和状态估计问题的一个联合解决方案。

（2）多目标数据关联与状态估计　在使用卡尔曼滤波或者粒子滤波进行多目标跟踪时，必须先解决匹配问题。最简单的匹配方法是最近邻方法。然而，如果多目标彼此接近，这种方法往往失效，最终会导致滤波方法无法收敛。目前由几种统计数据关联技术可以解决这个问题。联合概率数据关联滤波（JPDAF）和多假设跟踪（MHT）是两种广泛使用的数据关联技术。

①JPDAF：用一个测量值的序列定义轨迹，假设该测量值来自于同一目标。如果在时刻t存在N个轨迹，m个测量值Z（t）＝z1（t），…，zmt（t）。我们需要将这些测量值分配到现有的轨迹上。定义η是分配方案的集合，假设轨迹的数量保持不变。定义vi，l为关于轨迹l和测量zi的更新项。JPDAF将所有的测量值同每个轨迹关联起来，如果测量值zi（k）与轨迹l相关联，那后验概率的值为1，否则为0。权重更新的公式可以插入到每个轨迹的卡尔曼滤波和粒子滤波中。

Chang和Aggarwal使用这个方法从视频序列实现三维结构重建。Rasmussen和Hager对跟踪区域使用带约束的JPDAF滤波器。然而，该算法的主要缺陷是不能处理新进入视野（FOV）或退出视场的跟踪目标。由于JPDAF算法实现了两帧中固定数量目标跟踪的数据间关联，如果目标数量发生变化，就会导致严重的错误。接下来的多假设跟踪算法将会解决这个问题。

②MHT：如果只使用两帧建立运动的对应关系，很有可能会得到不正确的对应结果。如果直到检查了多帧之后，对应关系才判定，会得到更好的跟踪结果。MHT算法维持了对每帧中每个目标的几个对应关系的假设，最后目标跟踪是最相似的对应关系集合。该算法对进入视野的目标能够创建新的跟踪，对离开视野的目标能够终止跟踪。该算法也可以处理遮挡问题，即便跟踪目标消失了，跟踪还能够继续。

MHT是一种迭代算法，每次迭代都从当前一个跟踪假设开始。每个假设是一个不相交的跟踪集合。对于每个假设，需要预测每个目标在下一帧中的位置，计算预测和实际值之间的距离。基于距离度量为每个假设建立一个对应关系的集合，这将会为下一次迭代引入新的假设。基于当前的度量，每个新的假设表示一个新的跟踪集合。每个度量可以属于进入视野的新目标，或者之前跟踪的目标或者假的度量。而且，由于目标可以离开视野或者对应目标的度量值不能获得，度量值不能设置给目标。

确定意义上，MHT算法计算关联关系并枚举所有可能的关联。为了减少计算负载，Streit和Luginbuhl提出了概率MHT算法（PMHT）。关联关系被视为独立随机变量，故无需枚举所有的关联关系。近来，Hue等人提出了处理多度量跟踪多目标的粒子滤波器。该算法数据关联关系以类似PMHT的方式处理，状态估计通过粒子滤波获得。由于MHT算法是指数时间和空间的，为了解决这一问题，Cox和Hingorani利用Murty算法以多项式时间决定最优的k个假设跟踪兴趣点。Cham和Rehg利用多假设框架跟踪人的身体。

点跟踪方法可以基于是否产生了正确的点轨迹进行评估。基于真实值，可以通过计算准确率和召回率评价方法的好坏，其中准确率和召回率可以分别定义为：

另外，目标跟踪算法的量化比较可以从能否处理新目标进入和目标消失；能否处理目标被遮挡；能否提供成本函数最小化问题的最优方案三个方面实施。

点跟踪的一个重要的问题是处理目标消失和观测噪声。为了解决这些问题，确定的点跟踪算法经常使用运动约束，即共同运动或者近似一致性。统计点跟踪方法考虑了模型的不确定性能够处理噪声。这些不确定性通常假定具有服从正态分布的噪声。然而，测量值未必正态分布于预测值周围，且噪声参数未知。如果分布和噪声假设有效，卡尔曼滤波器和MHT就能够给出最优的解决方法。

处理噪声和观测消失的另一种可能的方法是强制约束目标的三维结构，如多体分解方法可通过强制目标点拟合三维目标的形状来处理带有噪声的观测值。Bregler等人用这个方法来解决非刚性目标的跟踪。他们首先基于一组可靠的跟踪定义一组形状基，所计算的形状基作为剩下的标为不可靠的点轨迹上的约束。点跟踪算法适合跟踪非常小的目标，那些目标可以用点表示。多点跟踪需要更大的目标。在使用多点跟踪多目标的过程中，属于同一目标的点自动聚类是一个重要问题，这是出于需要区分多目标与分辨背景和目标。基于运动的聚类或分割方法为了简化分割问题，通常假设点处于刚体上。