高温高压阀门通常采用楔形垫组合自紧密封结构(伍德密封结构)(见图2-6)和楔形密封垫结构(见图2-7)。
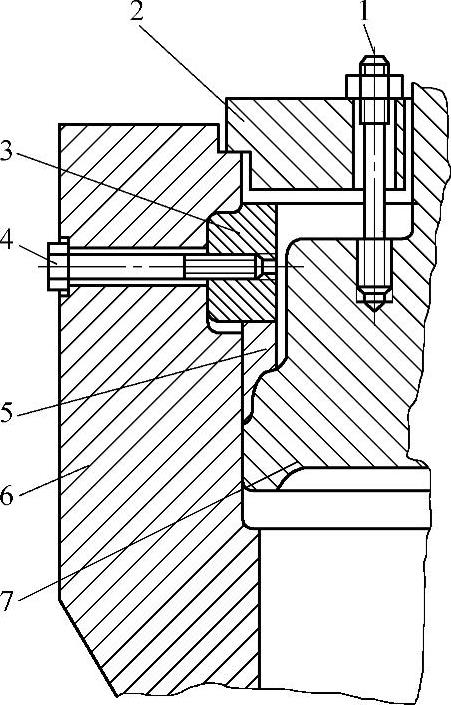
图2-6 楔形垫组合自紧密封结构(伍德密封结构)
1—预紧螺栓 2—支承环 3—四合环 4—拉紧螺栓 5—楔形密封垫 6—阀体顶部 7—阀盖
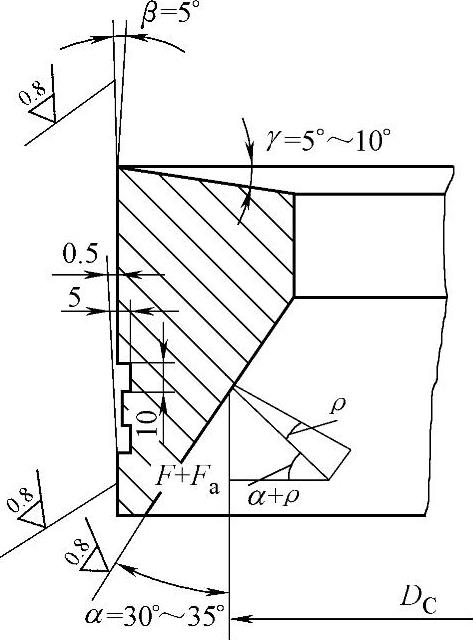
图2-7 楔形密封垫结构
阀盖和楔形密封垫之间按线接触密封设计,楔形密封垫的外锥面上开有1~2条环形沟槽。楔形密封垫的锥角分别为:α=30°~35°;β=5°;γ=5°~10°。
(1)载荷计算 内压引起的总轴向力为
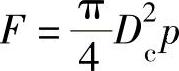
式中 F——内压引起的轴向力(N);
Dc——密封接触圆直径(mm);
p——设计压力(MPa)。预紧状态时,楔形密封垫密封的轴向分力,即预紧螺栓的载荷为
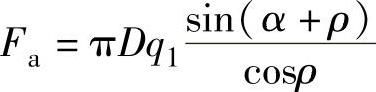
式中 Fa——楔形密封垫密封力的轴向分力(N);
q1——线密封比压,对碳素钢、低合金钢取q1=200~300N/mm;
ρ——摩擦角,钢与钢接触ρ=8°30′;钢与铜接触ρ=10°31′;钢与铝接触ρ=15°。
(2)支承环的设计计算 支承环结构如图2-8所示。
支承环结构尺寸确定后,需对作用于纵向截面的弯曲应力和a—a环向截面的当量应力进行强度校核。
纵向截面的弯曲应力校核:
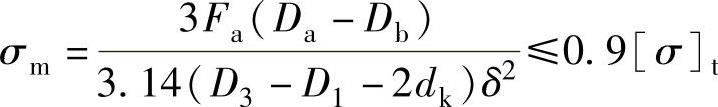
式中 σm——弯曲应力(MPa);
Da——a—a截面的直径(mm);
Db——螺栓孔中心圆直径(mm);
D3——支承环外径(mm);
D1——支承环内径(mm);
dK——螺栓孔直径(mm);
δ——支承环厚度(mm);
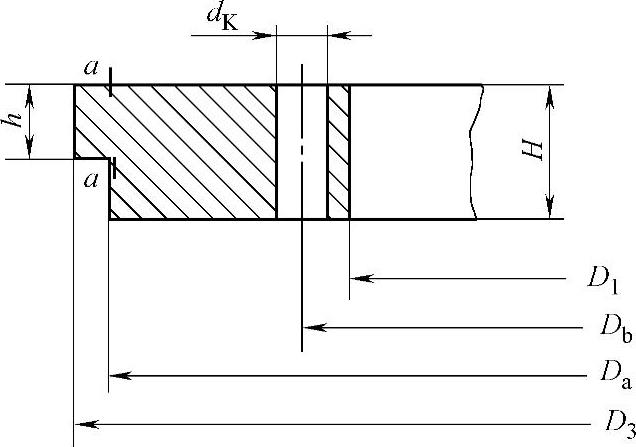
图2-8 支承环
[σ]t——设计温度下元件材料的许用应力(MPa)。
a—a环向截面的当量应力校核:
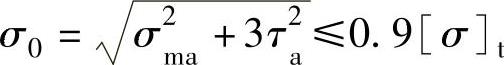
式中 σ0——当量应力(MPa);
σma——a—a环向截面的弯曲应力(MPa),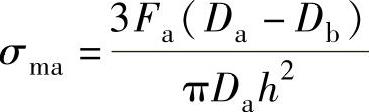 ;
;
τa——a—a环向截面的切应力(MPa),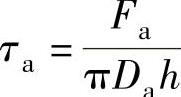 ;
;
h——厚度(mm),见图2-8。
(3)四合环的设计计算 四合环由四块元件组成,每块元件均有一个径向螺孔,如图2-9所示,计算时视为一个圆环。
对作用于a—a环向截面的切应力校核:
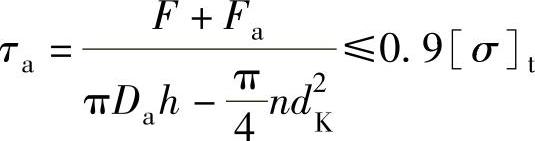
式中 Da——a—a截面直径(mm);
dK——拉紧螺栓孔直径(mm);
n——拉紧螺栓数量(mm);
h——厚度(mm),见图2-9。
(4)预紧螺栓的设计计算 预紧螺栓光杆部分直径计算:
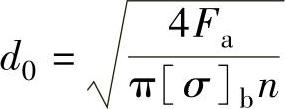
式中 d0——预紧螺栓光杆部分直径(mm);
[σ]b——常温下螺栓材料的许用应力(MPa);
n——螺栓数量。
(5)阀盖的设计计算 阀盖的结构如图2-10所示。
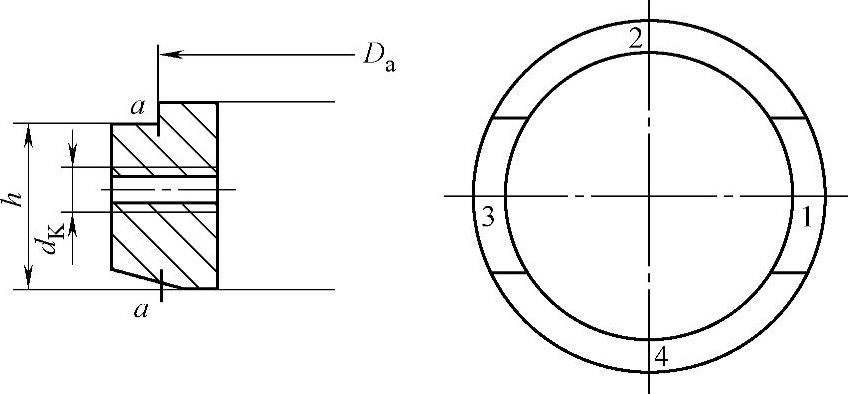
图2-9 四合环
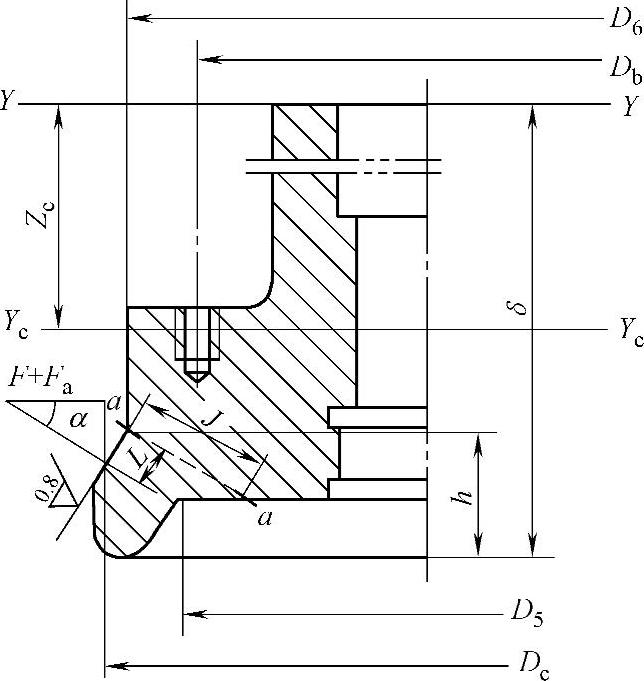
图2-10 阀盖
阀盖的结构尺寸确定后,对作用于纵向截面的弯曲应力和a—a环向截面的当量应力进行强度校核。
纵向截面的弯曲应力校核:
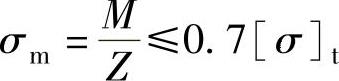
式中 M——纵向截面的弯矩(N·mm);
Z——纵向截面抗弯截面系数(mm3)。
M按下式计算:
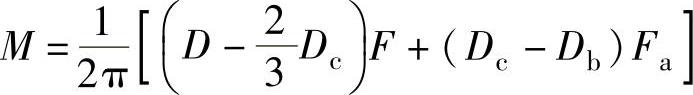
Z按下述方法确定:
当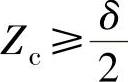 时,
时,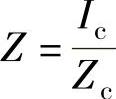
当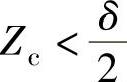 时,
时,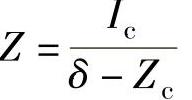
式中 Zc——纵向截面形心离截面最外端距离(mm);
δ——阀盖高度(mm);
Dc——密封接触圆直径(mm)。
a—a环向截面的当量应力校核:

式中 σma——弯曲应力(MPa);
τa——切应力(MPa);
σma按下式计算:(https://www.xing528.com)
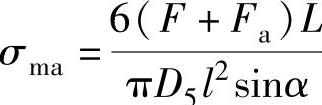
式中 D5——a—a环向截面的平均直径(mm)。
D5按下式计算:
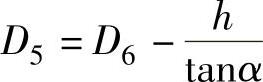
τa按下式计算:
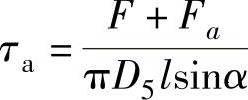
(6)阀体顶部的设计计算 阀体顶部结构如图2-11所示。
阀体顶部的结构尺寸确定后,需对作用于a—a和b—b环向截面的当量应力进行强度校核。
1)a—a环向截面的当量应力校核:
σoa=σa+σma≤0.9[σ]t
式中 σoa——a—a环向截面的当量应力(MPa);
σa——拉应力(MPa);
σma——弯曲应力(MPa)。
σa按下式计算:
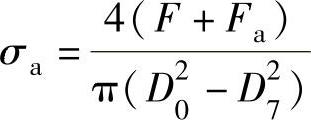
式中 D0——外直径(mm);
D7——直径(mm),见图2-11。
σma按下式计算:
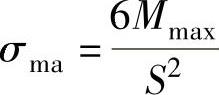
式中 S——a—a环向截面处厚度(mm)。
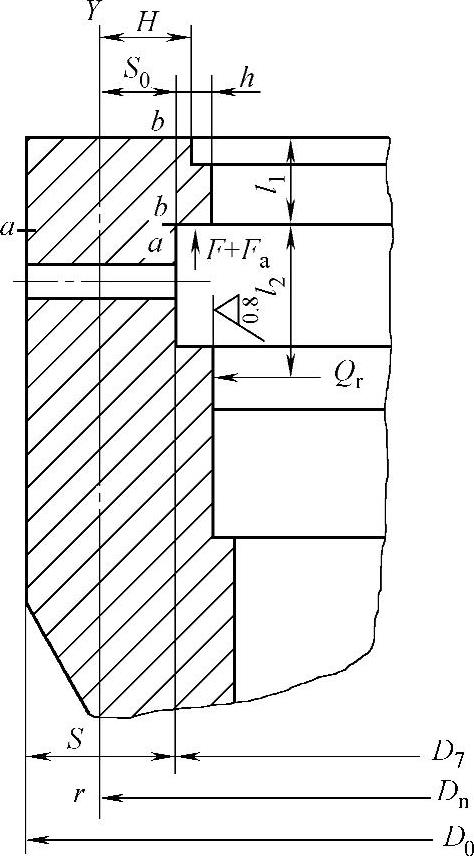
图2-11 阀体顶部
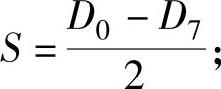
Mmax——作用于a—a环向截面单位长度上的最大弯矩(N·mm/mm);
Mmax按下列步骤计算:
①F+Fa引起的弯矩M按下式计算:
M=(F+Fa)H
式中 M——F+Fa引起的弯矩(N·mm);
H——力臂(mm),H=S0+0.5h;
S0——阀体顶部中性面Y—Y离直径D7的距离(mm):
当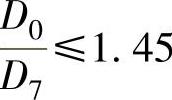 时,
时,
当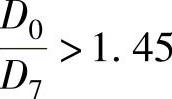 时,
时,
②中性面单位长度的弯矩:
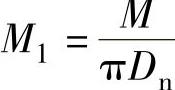
式中 M1——中性面单位长度的弯矩(N·mm/mm);
Dn——阀体顶部中性面Y—Y的直径(mm),Dn=D7+2S0。
③计算系数β:
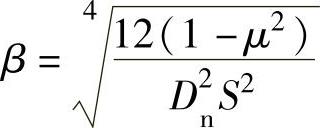
式中 β——计算系数(mm-1);
μ——平均壁温下材料的泊松比、当缺乏数据时,可取μ=0.3。
④根据βl1值查图2-12,得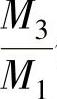 值和
值和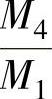 值。
值。
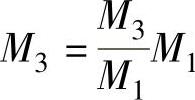
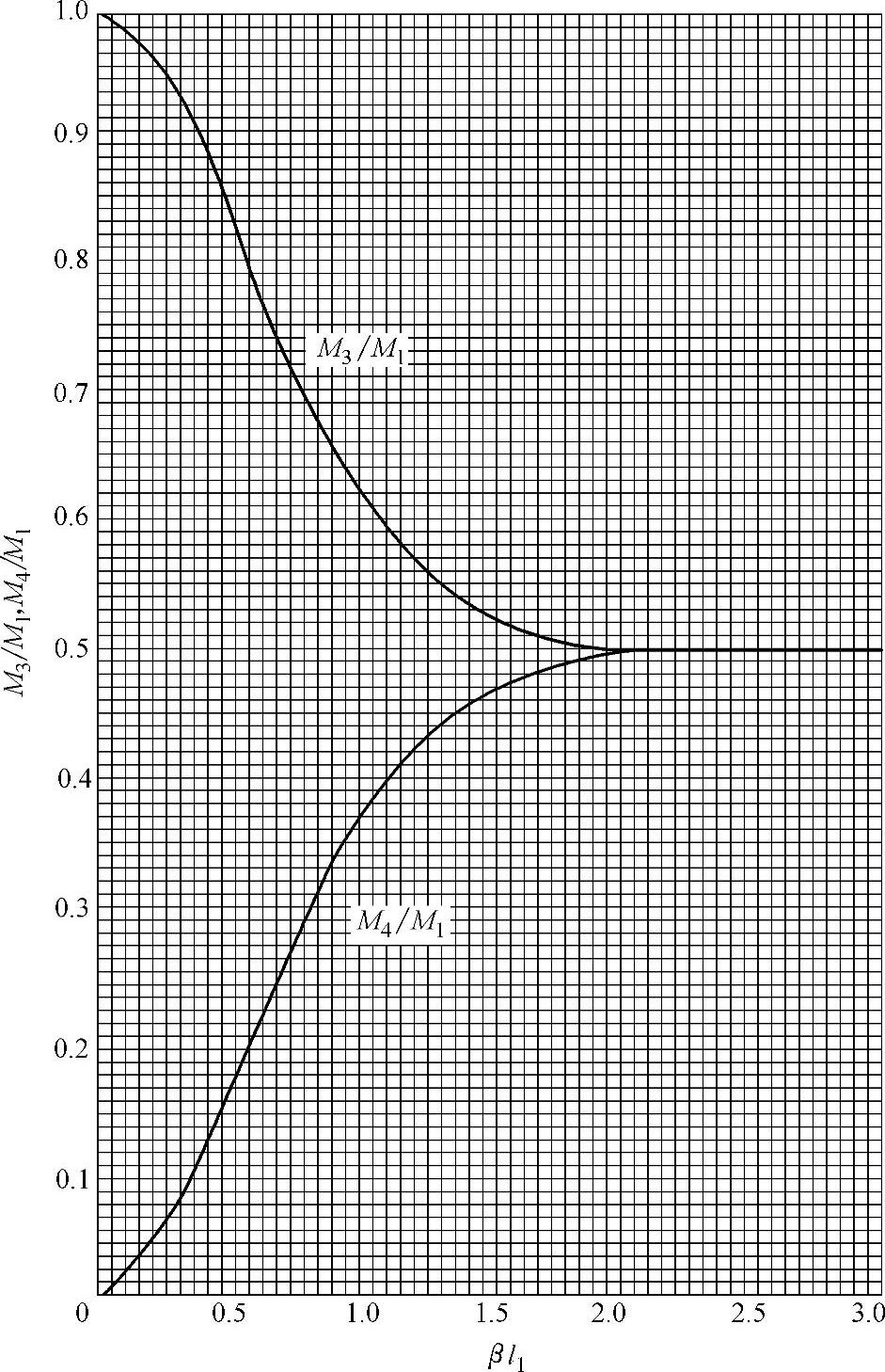
图2-12 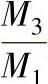 及
及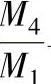 与βl1的关系
与βl1的关系
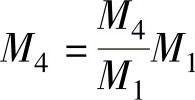
⑤计算系数C:
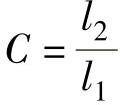
⑥根据βl1及C值查图2-13得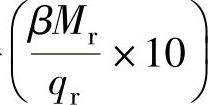 的值。
的值。
⑦沿中性面Y—Y单位长度上的径向载荷qr:
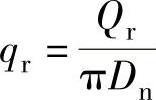
式中 qr——沿中性面Y—Y单位长度上的径向载荷(N/mm);
Qr——密封反力引起的径向载荷(N),
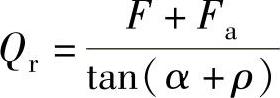
⑧计算弯矩Mr:
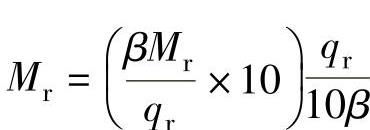
式中 Mr——计算弯矩(N·mm/mm)。

图2-13 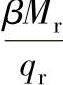 与βl1的关系
与βl1的关系
⑨最大弯矩Mmax取下式中绝对值较大者:
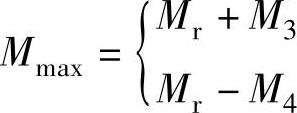
2)b—b环向截面的当量应力校核:
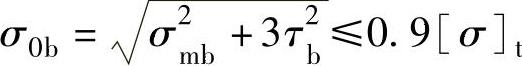
式中 σ0b——b—b环向截面的当量应力(MPa);
σmb——弯曲应力(MPa);
τb——切应力(MPa)。
σmb按下式计算:
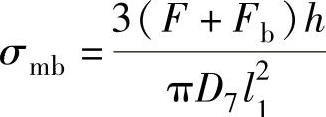
τb按下式计算:
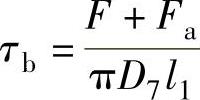
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




