并联变换器的载波移相技术

类比多电平变换器，另一种主流的变换器拓扑结构就是逆变器并联。在第6章中，载波移相（Interleaving）型PWM在并联变换器中的应用得到了介绍。载波移相型PWM通过两个逆变器之间开关函数的互相抵消，能够有效地抑制输入和输出电流纹波以及差模EMI噪声等^[10-12]。本节中将进一步介绍并联型逆变器及其PWM策略在抑制共模噪声上的作用。

图7-32所示是一个典型的三相并联逆变器拓扑结构。两个三相逆变器共用直流侧，并且通过耦合电感在交流侧连接。耦合电感的公共端输出给三相负载。耦合电感的作用是利用其主电感抑制两个逆变器由于输出电压不同带来的环流，并将两个逆变器输出电压平均后输出给负载。并联逆变器的共模电压如式（7-8）所示，即输出三相A、B、C相对直流母线电压的平均值，等价于两个逆变器输出电压的平均值。式（7-8）中六个相加量均为切换于V_dc/2和-V_dc/2之间的数字量。式（7-8）将传统三相逆变器共模电压由奇数个数字量相加转换为了偶数个数字量相加，在理论上存在共模电压为零的可能性。这一点和三电平逆变器类似却又不同。三电平逆变器是将每个二维数字量（+，-）变为（+，0，-）这样的三维数字量，从而实现了理论上零共模电压的可能性。在两个并联逆变器的空间矢量中，如果存在三个“1”和三个“0”，则共模电压保持为零。

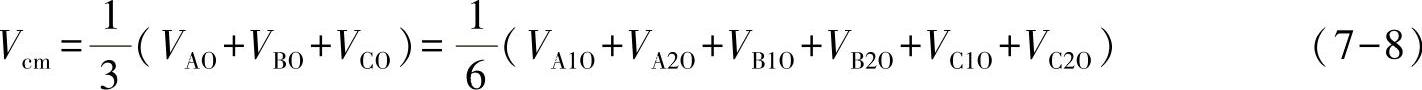
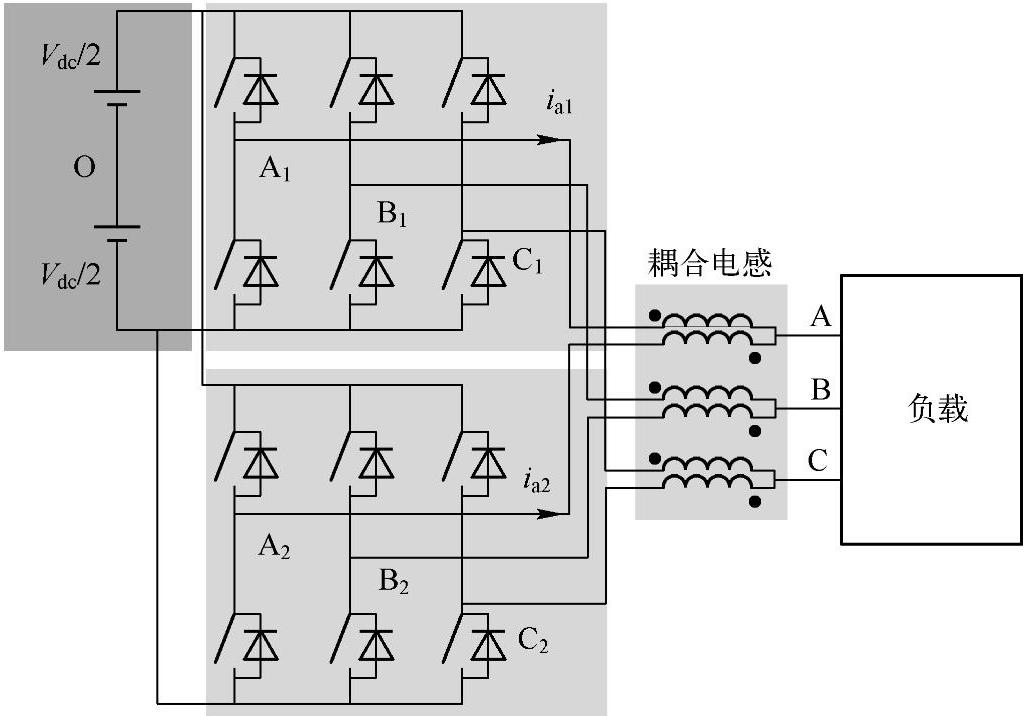
图7-32 并联逆变器拓扑结构

首先，分析载波移相PWM对共模电压的抑制作用。图7-33是180°载波移相PWM的原理图，在保持参考电压和占空比相同的情况下，将两个逆变器的载波移相180°，使逆变器2的输出脉冲由中间对齐改为两侧对齐，与逆变器1的输出脉冲形成交流移相的效果。第6章中分析了这样的移相方法可以在输入和输出开关纹波上实现对消的效果。

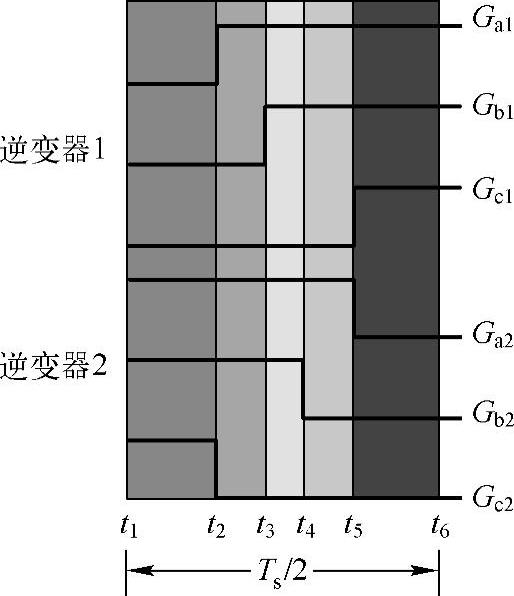
图7-34是分析180°载波移相方法对共模电压的影响。不失一般性，认为d_a≥d_b≥d_c。在图7-34中，半个开关周期内逆变器1和2的三相输出电压逻辑被分成了五段，其电压矢量和对应的共模电压见表7-3。在第1段中，逆变器1的输出电压矢量为000而逆变器2的输出电压矢量为111，因此共模电压为0。在第2段中，逆变器1的输出电压矢量为100而逆变器2的输出电压矢量为110，共模电压为0。在第3段中，逆变器1的输出电压为110而逆变器2的输出电压矢量为110，共模电压为V_dc/6。第4段中，逆变器1的输出电压为110而逆变器2的输出电压为100，共模电压为0。第5段中，逆变器1的输出电压为111而逆变器2的输出电压为000，共模电压为0。在开关周期的后一半中，开关顺序和共模电压将逆向重复前半周期的过程。

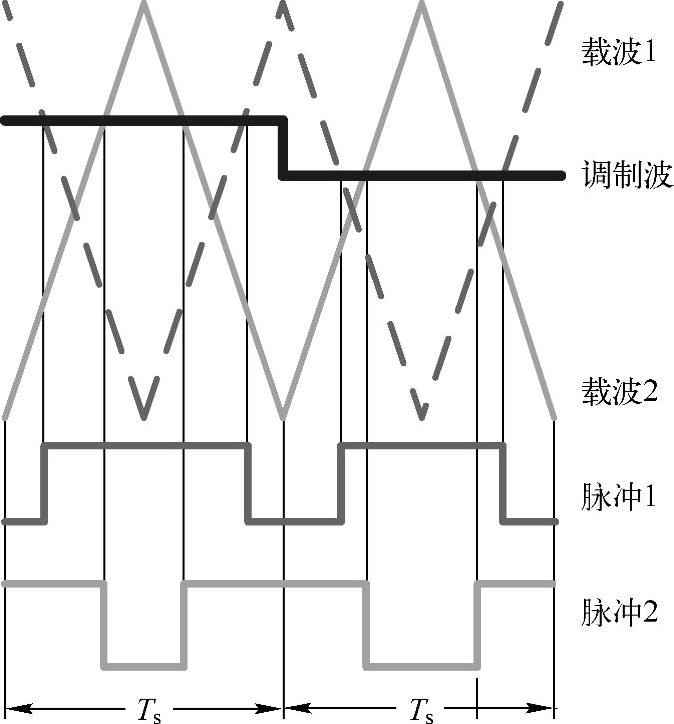
图7-33 载波移相PWM的原理

(www.xing528.com)

图7-34 载波移相PWM下半个开关周期的输出电压逻辑

表7-3 载波移相PWM后半个开关周期的电压矢量和共模电压

可以看出，在一个开关周期内并联逆变器的共模电压仅存在两个幅值为V_dc/6的窄脉冲电压。为了分析这两个窄脉冲，图7-35展示了空间矢量PWM的合成图。V₂和V₁矢量作用时间分别为d₂T_s和d₁T_s。由于这两者的不同，造成了表7-3中的第三段时间，长度为（d₂-d₁）T_s/2。因此存在共模电压不为零的一小段脉冲。如果d₂<d₁，共模电压在第三段将变为-V_dc/6，时间长度为（d₁-d₂）T_s/2。图7-36展示了d₂>d₁和d₂<d₁两种情况下一个开关周期的共模电压和共模伏秒。与普通三相逆变器共模电压在V_dc/2和-V_dc/2之间变换相比，载波移相PWM下的并联逆变器不论是共模电压幅值还是持续时间都明显得到改善。但是由于这两段幅值为V_dc/6的共模电压存在，共模噪声仍然是逆变器系统的一个主要问题，需要加入共模滤波器加以抑制。而这两段共模电压的伏秒积分又影响了共模电感的饱和等，成为滤波器设计中体积和重量的限制条件。

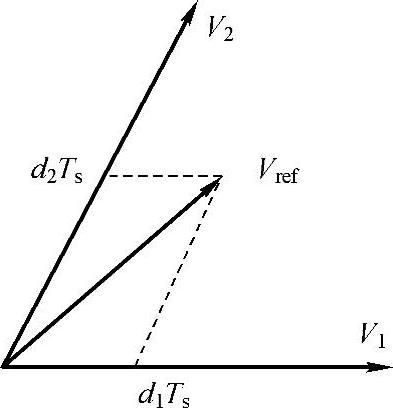
图7-35 空间矢量合成图

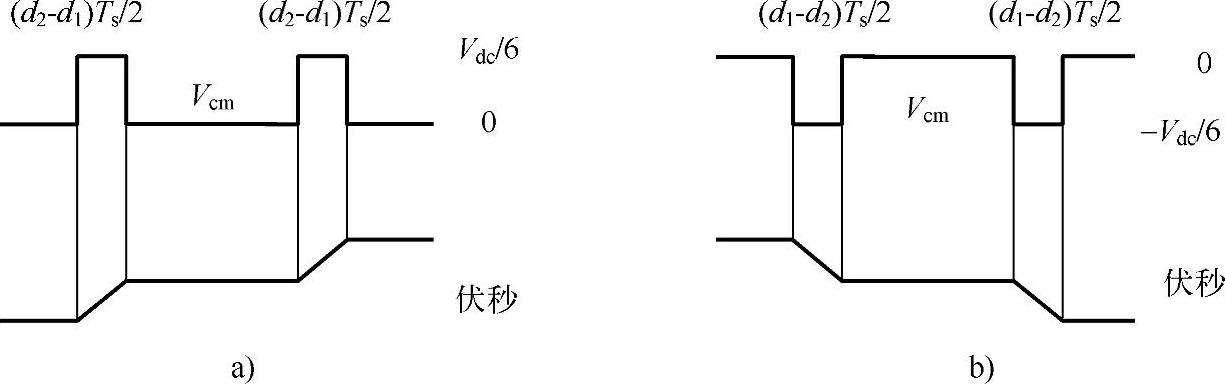
图7-36 采用载波移相PWM的并联逆变器共模电压和共模伏秒

a）d₂>d₁ b）d₂<d1