多电平变换器的零共模PWM技术

图7-19所示为一个典型的二极管钳位型（Neutral Point Clamped，NPC）三相三电平逆变器与负载连接的电路。每相桥臂通过四个开关的组合，可以分别实现与直流正母线、直流母线中点（O₁）以及直流负母线的连接。即每相输出电压相对O₁点可以有正母线电压（p）、零电压（o）和负母线电压（n）三种状态。这样，即使仍然是三相逆变器，三个桥臂输出的相对O₁的电压之和也可以为零。

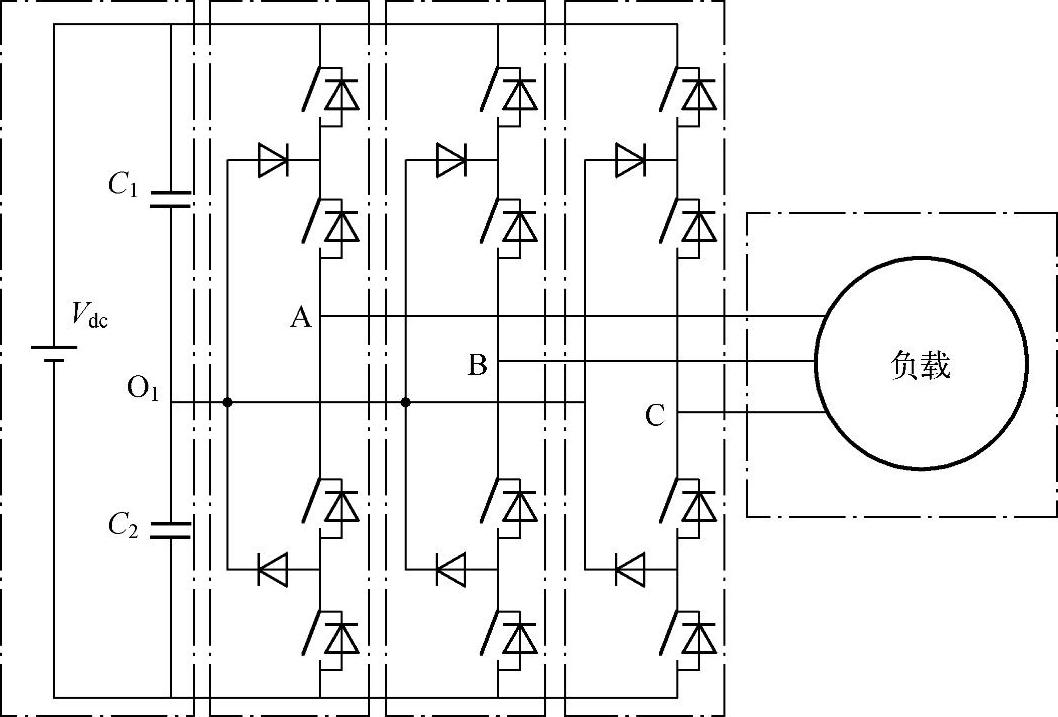
图7-19 典型的三相三电平逆变器与负载连接的电路

图7-20所示为三电平变换器的空间矢量分布。按照矢量的长度，可以分为大矢量（比如pnn）、中矢量（比如pon）、小矢量（比如poo）和零矢量（包括ppp、ooo和nnn三种）。其中，用粗线标出的六个中矢量（pon、opn、npo、nop、onp和pno）恰好都是由p、n、o三种状态组成的，它们对应的共模电压恰好为0。同时，三个零矢量中，ooo矢量对应的共模电压也为0。这样，利用这七个矢量实现参考电压的合成，就可以保持在整个开关周期内共模电压为0；而六个中矢量恰好把电压空间等弧度划分为6个扇区，参考电压矢量就可以由所在扇区相邻两个中矢量以及ooo矢量合成实现，这样的合成方式与两电平空间矢量类似。实验结果表明，应用这样的调制方式，系统的共模电压可以明显下降，这是因为系统非理想特性造成了少量共模分量^[8，9]。图7-21所示为三电平变换器的共模电压比较的实验结果，可以看出普通SVPWM下三电平变换器共模电压存在脉冲序列，而零共模PWM下的共模电压除了少量毛刺外，基本控制在零附近。

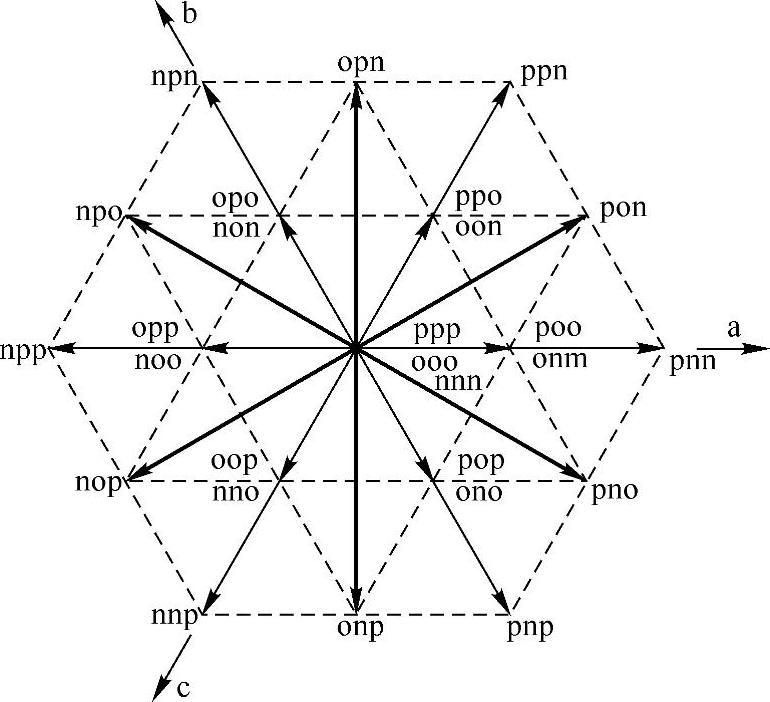
图7-20 典型的三相三电平逆变器的空间矢量分布

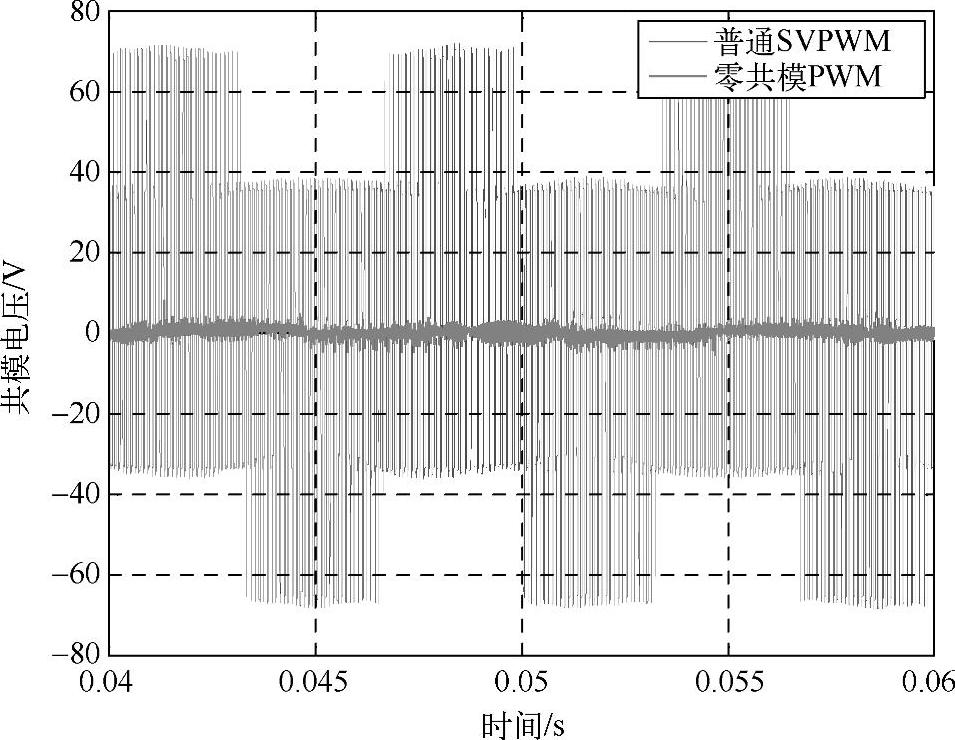
图7-21 实验结果中的三电平变换器共模电压比较（普通SVPWM与零共模PWM）(www.xing528.com)

三电平零共模PWM的算法亦可用以正弦脉宽调制（SPWM）为代表的载波比较的方法来实现。普通的三电平主要采用同相载波层叠法，而零共模则采用类似于两电平的单载波法^[8]。如图7-22所示，三相对称的正弦参考波V₁、V₂、V₃与在±1之间变化的三角载波V_r比较得到参考信号V_g1、V_g2、V_g3，再根据式（7-3）确定三相桥臂的驱动参考信号V_a、V_b、V_c，显然式（7-3）中三相电压之和恒为零，即输出的共模电压为零。

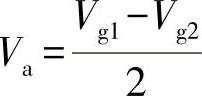
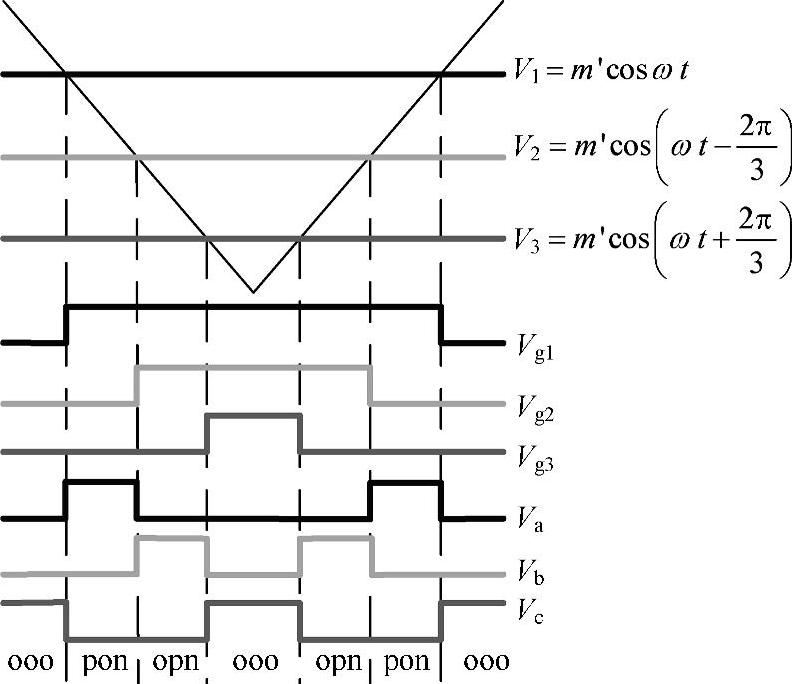
图7-22 三电平零共模载波比较PWM的驱动信号产生原理

在实际应用中，由于载波比较PWM算法简单，易于实现，故常用以等效实现SVPWM。一般情况下，SVPWM在每个载波周期内采用七段式的矢量安排顺序（零矢量→有效矢量1→有效矢量2→零矢量→有效矢量2→有效矢量1→零矢量），显然与图7-22中载波比较产生的矢量顺序完全一致，因此只需证明各段的作用时间相同即可。空间矢量调制可用矢量合成的原理计算矢量作用时间，而载波比较的方法利用平面几何的知识也可计算作用时间。不论从理论计算还是伏秒平衡的角度解释，两种调制方法的有效矢量和零矢量的作用时间都是一致的。两种PWM唯一的区别在于零矢量在中心与两侧的分配比例不同，而载波比较法可以通过零序分量的注入改变零矢量在中间及两侧的作用时间而不影响有效矢量的分配，从而实现与零共模SVPWM的完全等效。其等效的方法就是在三相平衡的参考波V₁、V₂、V₃内注入零序电压分量v_z=-0.5（v_max+v_min），其中v_max（v_min）表示三相参考波瞬时值最大（小）的一相。

然而零共模情况下两种PWM的等效理论与普通三电平的两种PWM调制的等效原理有两点不同。其一，如图7-22所示，最终产生的A相驱动波形是V₁与V₂之差除以2，即线电压的一半。那么最终A相的基波电压幅值仅是调制波V₁的0.866同时相位超前30°，图7-22中三相对称参考波的调制比m′并非真正的调制比，真正的调制比只有普通SVPWM的0.866，这也解释了直流母线电压利用率降低的原因。第二，如图7-20所示，对6个中矢量进行矢量编号（SV₁～SV₆）。虽然在一次矢量合成中，两个中矢量发送的先后次序对输出的宏观特性没有影响。但是为了使两种PWM达到完全一致的等效，现给出空间矢量调制时发送中矢量次序的规律：在每个载波的前半周期总是先发送该扇区中下标为奇数的中矢量再发送下标为偶数的中矢量，后半周期的发送次序与前半周期对称。根据两种PWM的等效规律，便可以用载波比较的方式消除共模电压，从而简化控制算法。