技术的应用：并联逆变器和载波移相PWM

如6.1节所述，并联逆变器可以通过分别合成参考矢量来实现，也可以通过载波比较来实现。本节所述的载波移相PWM实际上是一种通过利用载波比较的方法改进PWM性能的方法。下一章介绍并联逆变器的零共模PWM则会采用空间矢量合成的思路。由于共模抑制是独立章节的内容，因此本节不再详细介绍。

本节介绍的载波移相PWM是基于图6-2c所示的并联结构实现的。本节的最后部分也会介绍如何将载波移相PWM应用在多模块电机上，通过电机结构实现并联的效果。

图6-14所示是最基本的载波移相结构^[14]。对于两个并联的电力电子变换器，对应的载波在一个开关周期的间距为2π，载波移相示意图如图6-14a所示。当两个变换器的载波移相κ时，对应的开关时序也会有相应的延迟。两个变换器的输出PWM电压就会存在差别。这个差别在变换器上产生两个效果：经过耦合电感之后的公共端输出电压将在原始PWM电压的基础上产生对消效果，谐波得到改变，如图6-14b中的输出电流i_A；两个变换器的电压差也通过耦合电感产生环流，在两个变换器之间流动，即图6-14b中的i_A1与i_A2之差。

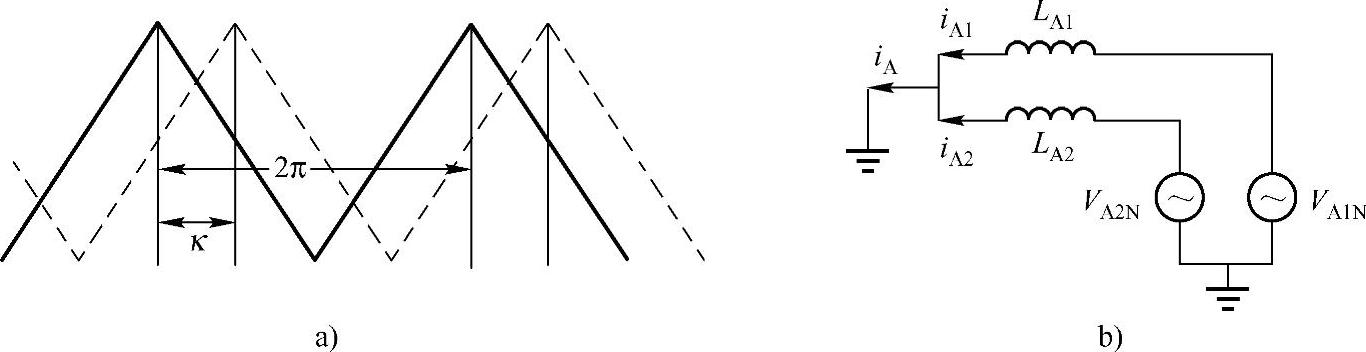
图6-14 并联变换器载波移相的基本原理

a）载波移相示意图 b）简化等效电路

如本书第2章简单介绍的分析方法，可以对载波移相PWM的输出电压进行双傅里叶变换。以基波频率ω₀、载波频率ω_c为例，图6-14b中的输出电压V_A1N如式（6-1）所示，表示m次谐波加n次基波所在频率的分量。C_mn是幅值，θ_c和θ₀指的是基波和载波的初始角度。当第二个变换器的载波移相κ时，其输出电压V_A2N就可以用式（6-2）表示。此时，两个电压的平均值V_AN=1/2（V_A1N+V_A2N）就是输出端口的等效电压。

V_A1N（m，n）（t）=C_mncos[（mω_c+nω₀）t+mθ_c+nθ₀] （6-1）

V_A2N（m，n）（t）=C_mncos[（mω_c+nω₀）t+m（θ_c+κ）+nθ₀] （6-2）

图6-15所示为输出端口电压V_AN的合成在第m次开关频率的原理。图6-15a所示为无载波移相的情况：此时两个电压分量所在的矢量是同相位的，等于代数叠加。因此输出的对应谐波含量是最大的。图6-15b所示为存在载波移相κ时的合成，此时两个电压源对应谐波分量的矢量存在mκ的相位差，是矢量合成，输出对应次谐波相对前者可以减小。

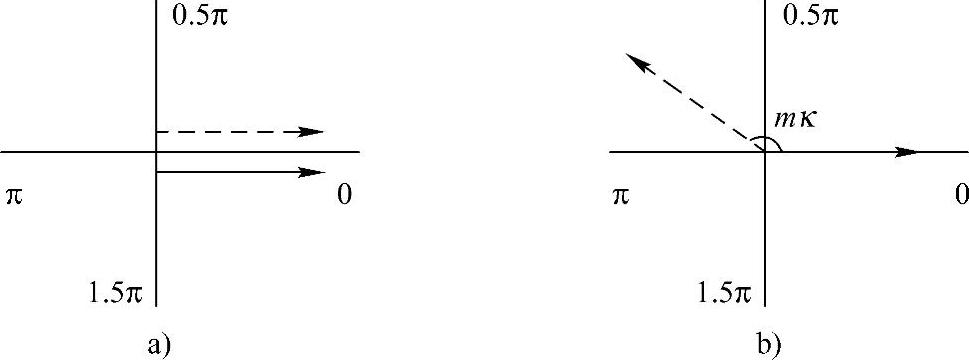
图6-15 并联变换器输出电流开关m次谐波的矢量合成图

a）无载波移相 b）载波移相κ[14]

因此，可以利用图6-15的原理，设计合适的移相角度κ来消除对应次谐波的含量。最简单的例子就是设置κ=π，这样第一次开关频率对应的谐波在图6-15中就是互差180°的矢量相加，理论上等于零。其他奇数次开关频率也都是对消的情况。而偶数次开关频率下两个矢量将重合，与无移相的情况类似。这样并联变换器的输出电流中将消除奇数次谐波分量，大大改善了输出电流的质量。而如果为了抑制开关频率的偶数次谐波，则可以设置κ=π/2。这样m为偶数时，图6-15b中的谐波矢量实现了对消。因此，对不同的消除谐波要求可以设置不同的移相角κ。电流谐波中开关频率的奇偶次分量的比重随调制比的变化而变化。图6-16所示为不同移相角κ下谐波畸变率THD的衰减（残余）率随调制比的变化。可以看出，调制比增加的情况下，采用κ=π的移相角，谐波改善越多；采用κ=π/2的移相角，谐波改善越少。因此，不同的调制比下存在最优的移相角κ使谐波的改善达到最佳[14]。

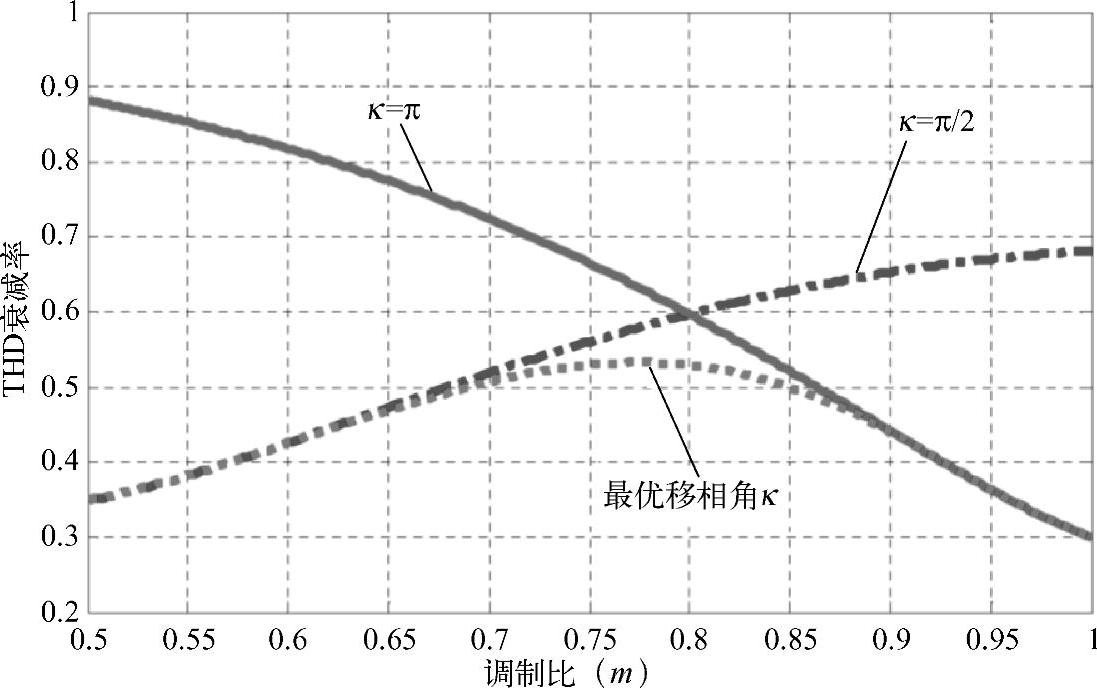
图6-16 不同移相角κ下THD衰减率随调制比的变化[14]

另外，由于负载的特性不同，载波移相的效果也会有所不同。尤其在传导回路中存在谐振点的电路，需要特别消除谐振频率附近的谐波。因此移相角也会根据这些要求设计^[15-17]。

实验结果能够清晰地反映载波移相的消除谐波效果。图6-17所示为并联变换器交流侧输出电流的波形。图6-17a所示为无载波移相的结果，三相电流中存在丰富的谐波，如图6-18a所示。采用κ=π的载波移相后，图6-17b所示的电流中纹波大大减小。THD从21.2%降到6.7%，但是基波电流基本保持不变。从图6-18b可以看出，主要的奇数次谐波都被抑制了。

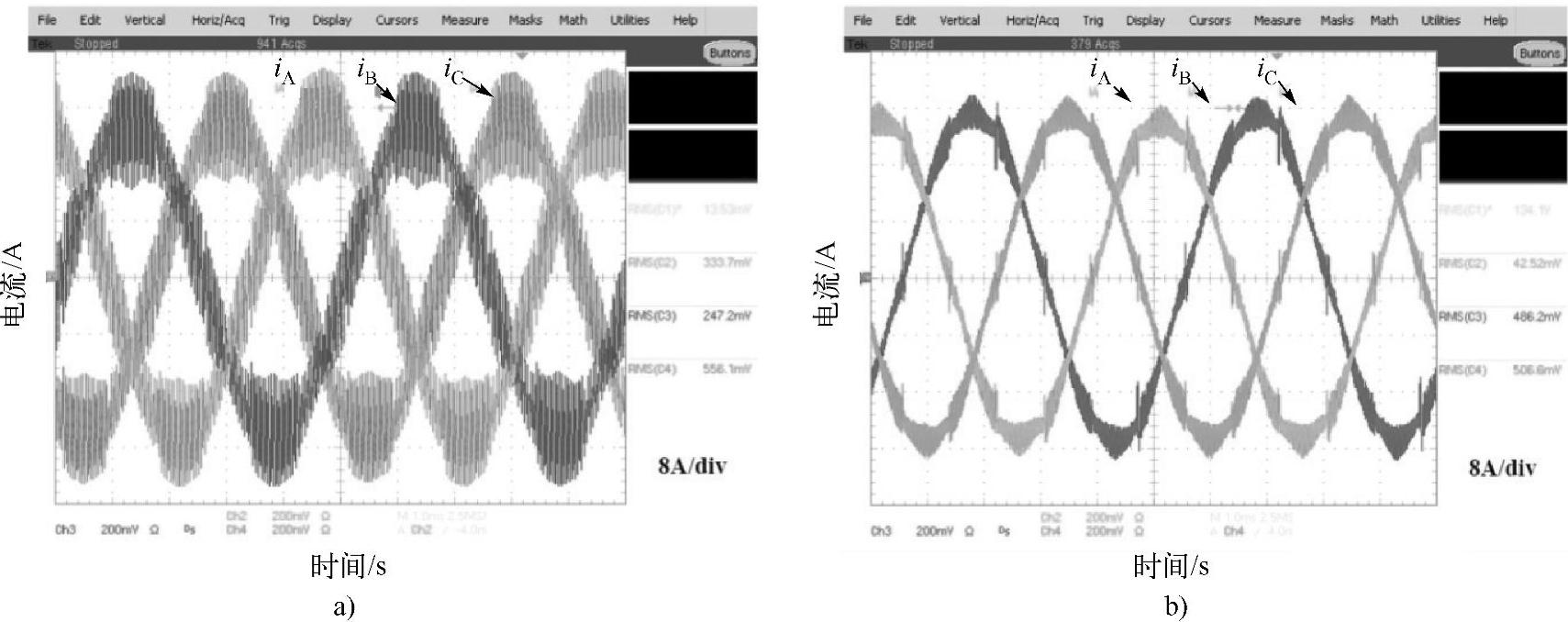
图6-17 并联变换器输出电流实验结果

a）无载波移相 b）载波移相κ=π[14]

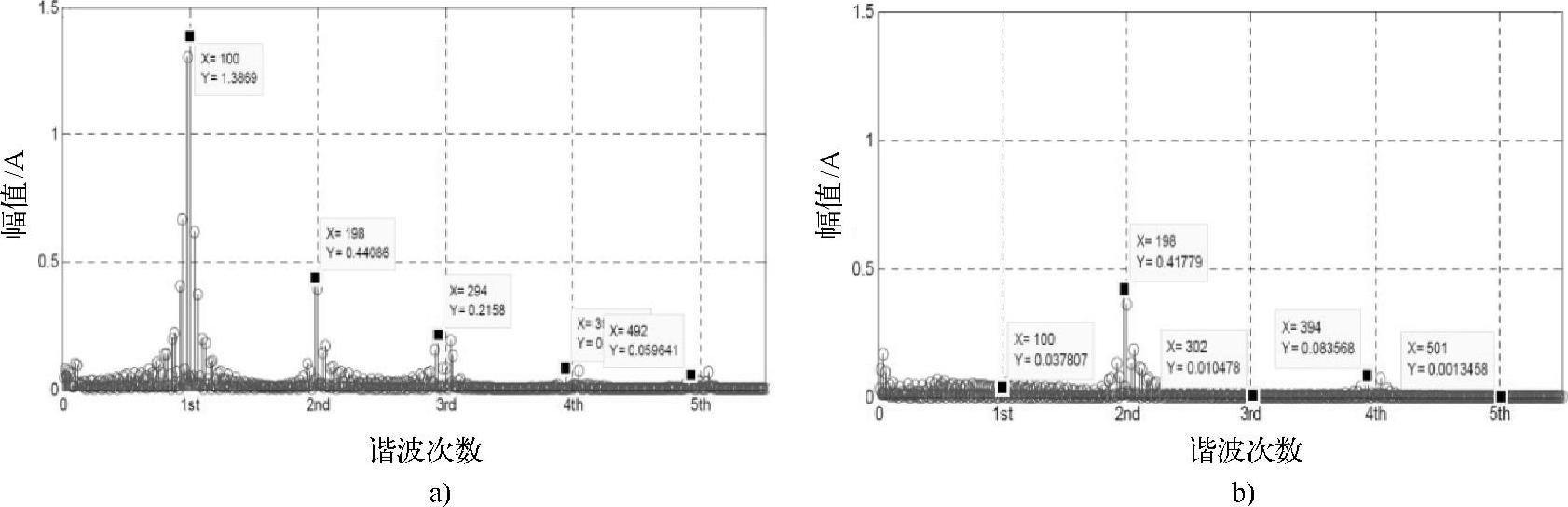
图6-18 并联变换器输出电流频谱分析

a）无载波移相 b）载波移相κ=π[14]

由以上论述不难看出，采用载波移相的方法，可以有效地抑制开关频率相关的部分谐波和电磁干扰，因此对系统滤波器的设计也有对应的优势。但是为了抑制两个逆变器之间的电压差产生的环流，也需要增加环流抑制电感，即图6-2c中标注的耦合电感。从数学上解释，式（6-1）与式（6-2）相减得到的电压差需要有阻抗抑制，否则环流将会无穷大。幸运的是由于载波移相PWM中两个变换器的参考电压是一致的，仅仅变换了载波的相位，因此两个变换器电压之差也在每个开关周期内实现了平衡，或者说电压之差只存在开关次及其以上的频率。式（6-1）与式（6-2）相减通过和差化积得到的结果也可以证明这一点。因此，耦合电感只需要抑制开关次的环流，可以设计得较小。图6-19所示就是一个典型的耦合电感结构。采用两个U形磁心组合而成的耦合电感，通过反向绕线实现。这种情况下，两个逆变器之间的环流产生的磁链将沿图6-19中磁心的主回路流动，而各自电流独立产生的磁链沿图6-19的漏磁通传导。因此，耦合电感的主电感作为环流抑制电感，而漏感对负载的影响也较小。并联变换器对于共模噪声抑制的方法以及对应的并联耦合电感的问题，在第7章还会描述。

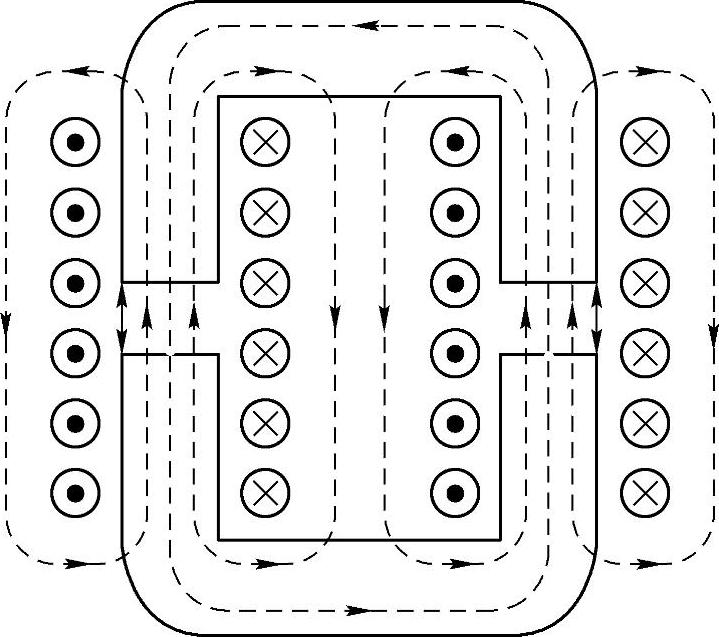
图6-19 典型的耦合电感结构[14]

以上描述的都是典型的三相负载下的并联变换器载波移相PWM技术，通过载波移相对消部分谐波分量实现输出谐波和EMI的改善。而这种思路还可以用于非常规的负载，即通过负载本身实现并联而不需要采用耦合电感的方式改善负载的谐波特性。图6-20所示就是一种非常规的负载：多模块三相电机。在电机中有N个三相模块，由N套三相绕组通过N个驱动电路所驱动。这实际上等于通过电机本身将N个变流器并联在一起，最后实现功率和转矩的累加。(www.xing528.com)

如果对于这N个驱动变流器也采用载波移相的控制方法，则可以在输出转矩上实现脉动转矩开关频率分量的对消效果。实际上，交流电机的电磁转矩的主要谐波分量是开关频率的二次谐波，因此主要对消目标也是二次开关频率的转矩纹波分量。图6-21所示就是N个驱动变流器的载波移相方法。从第一组载波开始，相邻两组载波之间存在1/（2N）开关周期的时间差，即π/N的相位差，最终得到N组载波。此时，每两组相邻载波在对应的变流器产生的电流谐波在时域上就会相差1/（2N）开关周期，而二次开关频率分量在相频特性上也有2π/N的相位差。由于每部分产生的转矩是由电流直接产生的，相邻两个模块产生的转矩在二次开关频率上也会有2π/N的相位差。

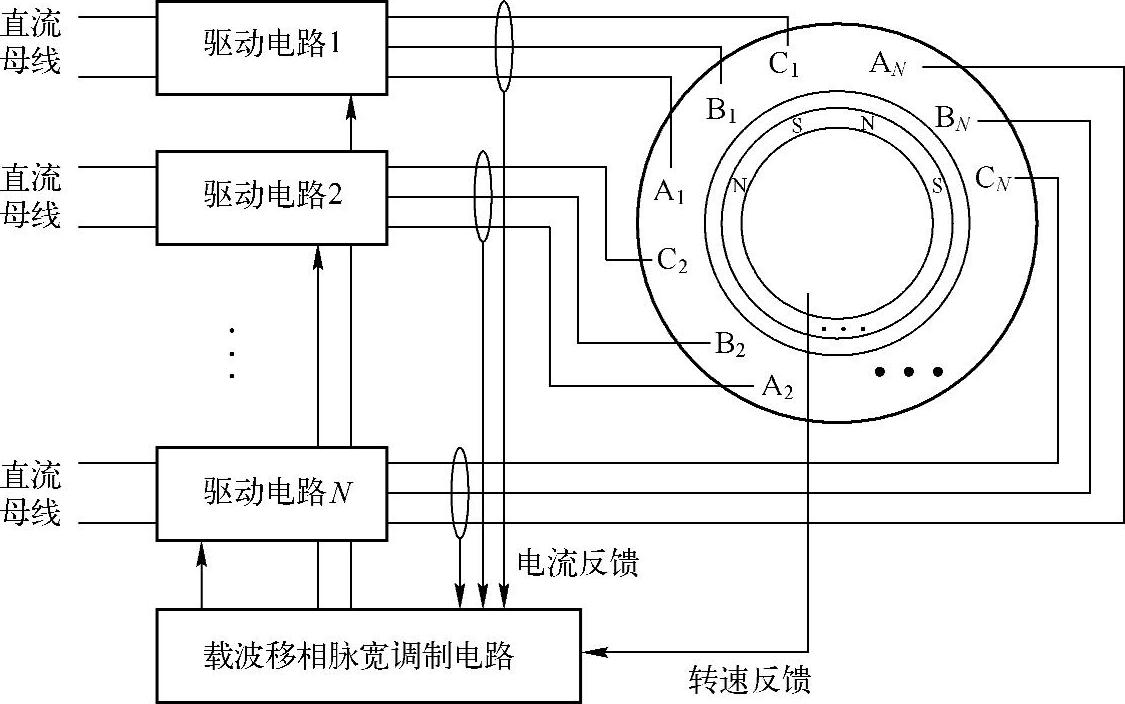
图6-20 模块并联驱动电机结构图

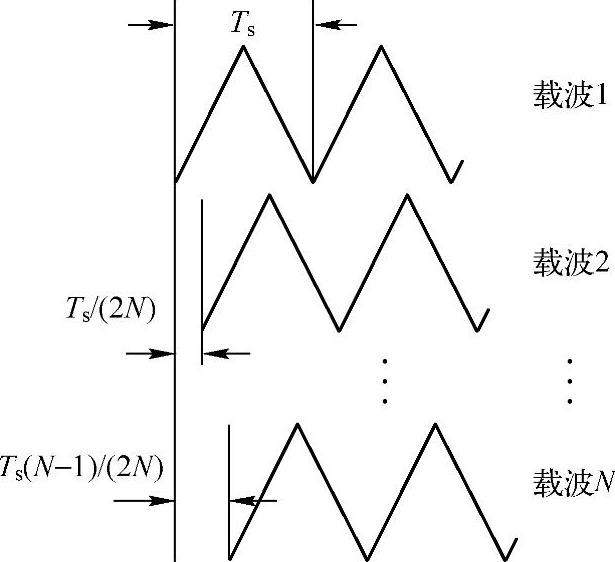
图6-21 N模块载波移相结构图

图6-22所示为二次开关频率分量转矩合成的原理图。当没有载波移相时，各个模块转矩分量是同相位的，因此合成转矩等于代数相加的结果，即近似为每个模块转矩的N倍，如图6-22a所示。采用图6-21所示的载波移相时，二次开关频率下的相邻模块产生的转矩分量互差2π/N，合成转矩将表现为矢量相加，最后理论上等于零，如图6-22b所示。因此，载波移相PWM下电机对应的转矩脉动将明显改善。

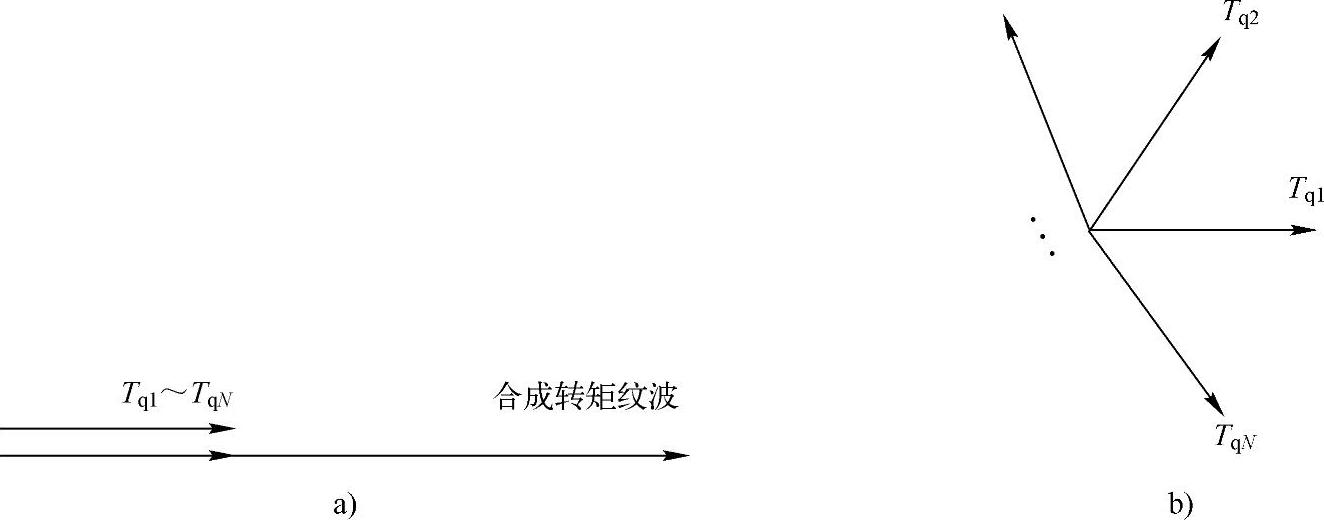
图6-22 转矩纹波合成原理图

a）载波不移相 b）载波移相

图6-23所示为一个双逆变器并联驱动两模块电机的电磁转矩时域波形仿真结果。可以看出四组转矩的开关纹波在时域上互差1/2开关周期，合成转矩上开关频率分量实现了对消。

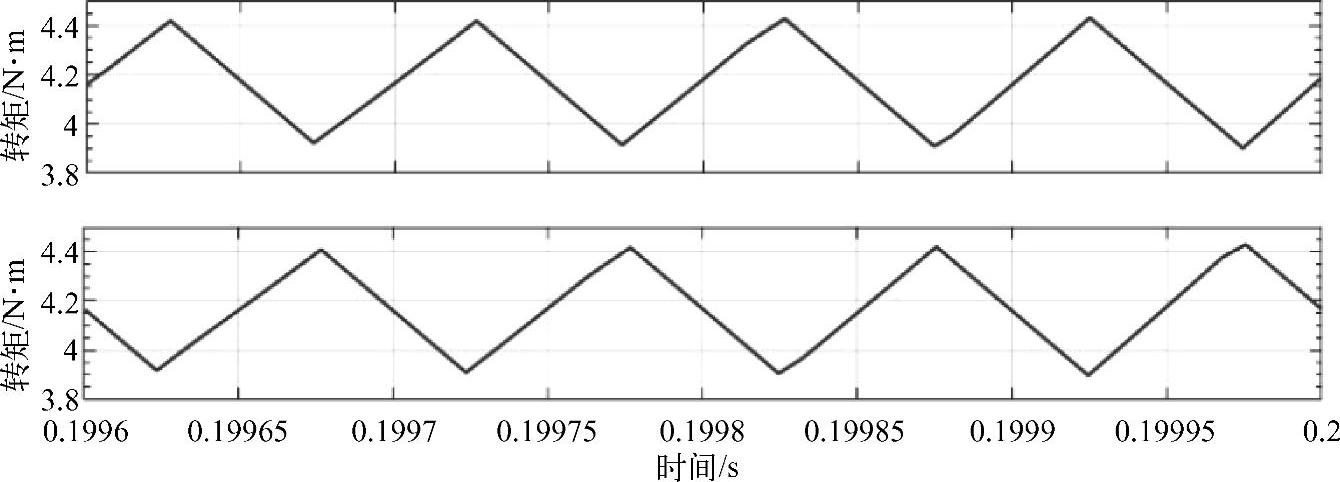
图6-23 两模块电机驱动的仿真结果

图6-24所示是两组转矩的FFT分析。两组转矩在二次开关频率附近的分量幅频响应近似一致，但是相频特性依次错开180°。频域分析的结果印证了时域转矩纹波对消的原理。

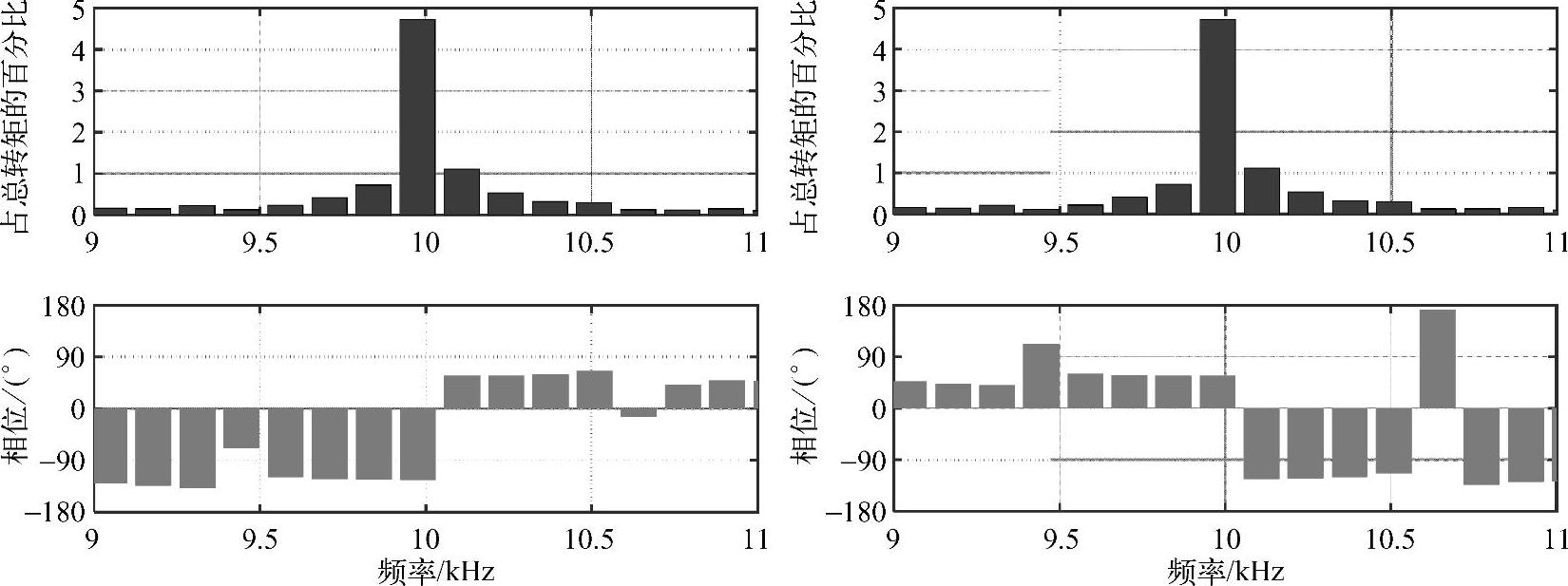
图6-24 两组转矩的FFT分析

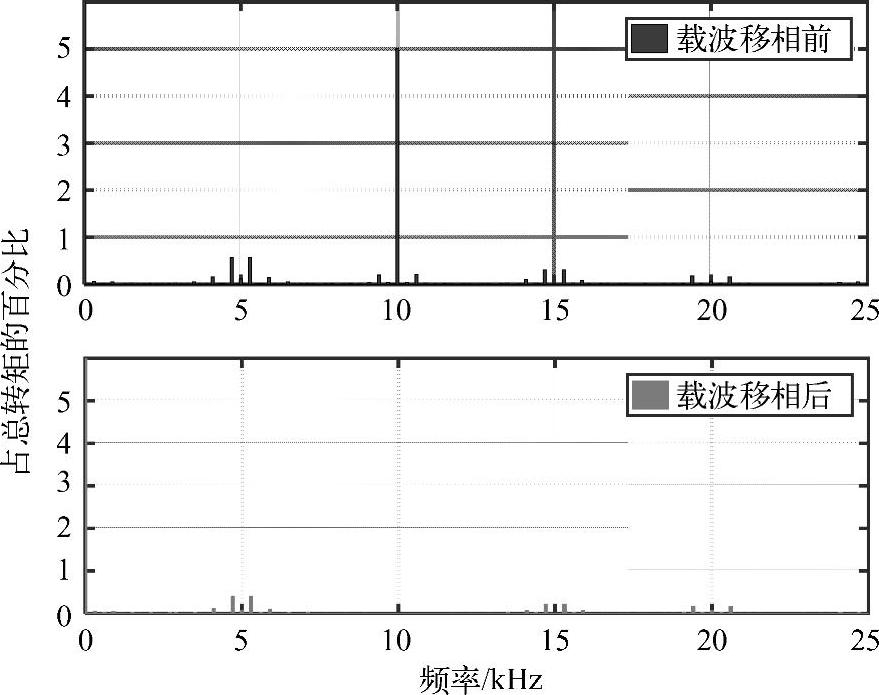
图6-25 未采用载波移相和采用90°载波移相的转矩的FFT幅频响应比较结果

图6-25所示是未采用载波移相和采用90°载波移相的转矩的FFT幅频响应比较结果。在未采用载波移相时，转矩脉动的主要分量集中在二次开关频率（10kHz）附近，幅值约为平均转矩的5%（上图）；采用90°载波移相后，由于两个模块产生的转矩在10kHz的分量幅值相等、相位相反，合成之后实现了对消，所以合成的转矩在10kHz附近被大大减小（下图）。此图证明了载波移相的效果。

多模块电机控制实验结果有效地验证了载波移相对转矩纹波的消除效果。以两模块电机为实例，采用传统矢量控制，开关频率为5kHz。这里要强调的是，两模块电机在未采用载波移相前，将等同于一台普通的三相电机。图6-26所示为不同模块在载波移相前与载波移相后的a相电流的波形。可以清楚地看出在移相后两个模块电流纹波在时域上错开一个角度。图6-27所示是实验测得的电机转矩脉动频谱分析结果，采用90°的载波移相后，转矩纹波大大减小，其中主要频次的10kHz谐波及其边带基本完全消除。图6-28所示是实验测得的未采用载波移相和采用90°载波移相的转矩时域波形，在采用了多模块电机结构控制后，整个电机转矩脉动大大减小。

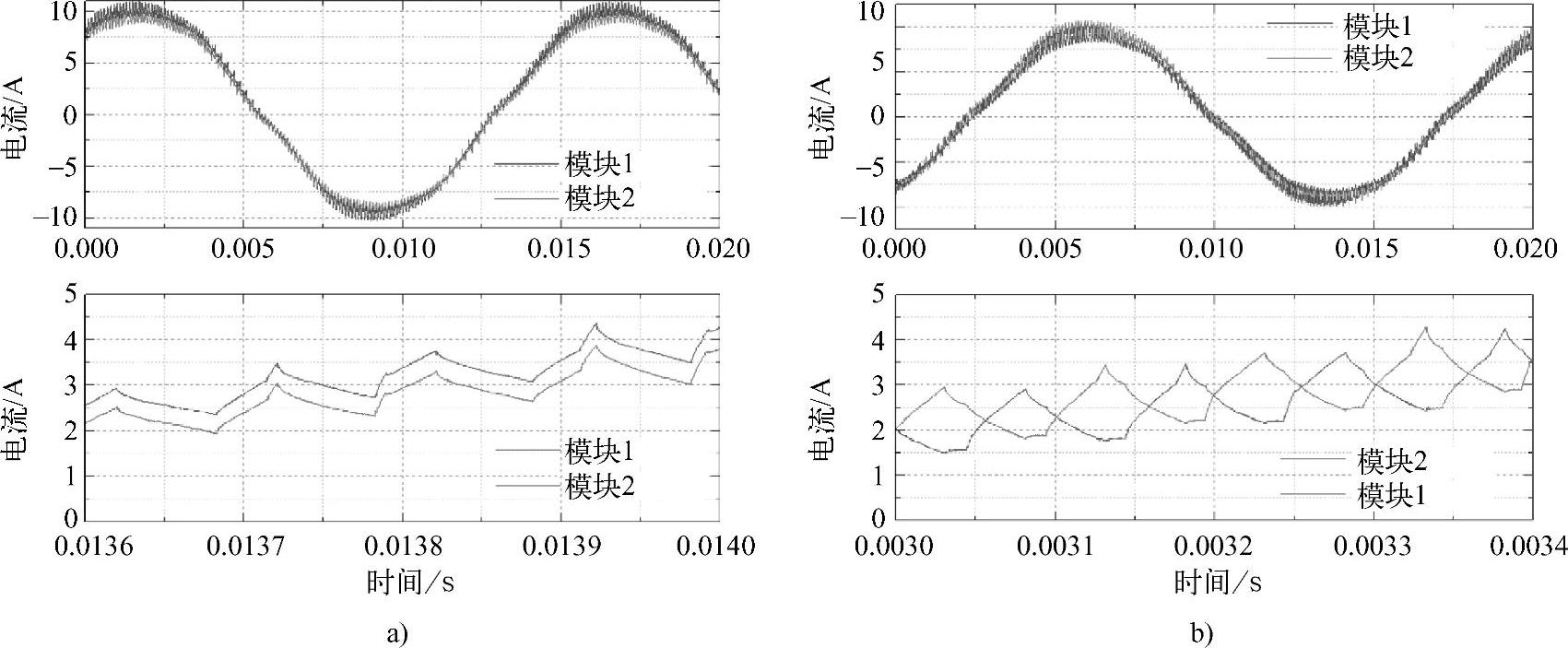
图6-26 实验测得的电流纹波对比

a）未采用载波移相 b）采用90°载波移相

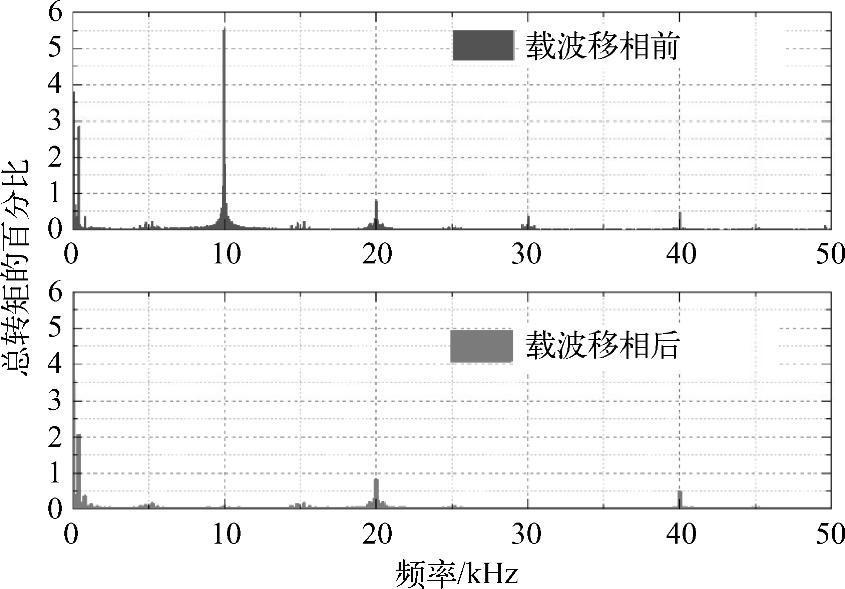
图6-27 实验测得的未采用载波移相和采用90°载波移相的转矩幅频响应对比

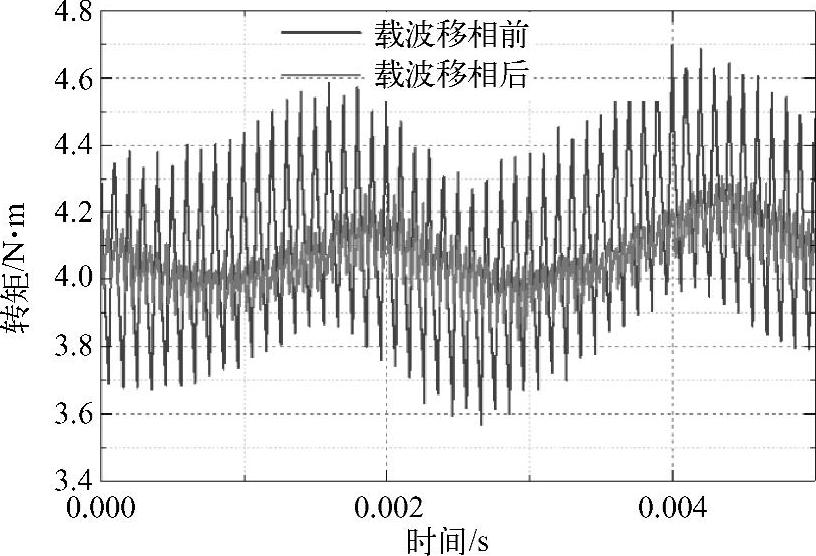
图6-28 实验测得的未采用载波移相和采用90°载波移相的转矩时域波形（见文后彩插）