通用多相变换器电流纹波预测方法优化

4.2节中介绍的基于每个开关矢量的戴维南等效电路的电流纹波预测方法对三相变换器是比较适用的方法，但是对于较为复杂的多相逆变器则存在明显的缺陷。两电平n相电压型变换器的开关矢量总数目为2ⁿ，因此，对于多相变换器，电压矢量数量将急剧增加。例如，五相变换器存在32个电压矢量，六相变换器存在64个电压矢量。继续采用4.2节中的对每个开关矢量均做戴维南等效电路并得到电流纹波变化率解析表达式的方法将变得很困难，同时将增加控制器硬件的计算负担。

本节介绍一种更为通用的多相变换器电流纹波预测方法，不需要对每个开关矢量均求戴维南等效电路，而是通过通用的等效电路求解电流纹波。该方法对于多相变换器的电流纹波预测将大大简化。

图4-24展示的是一个典型的n相电压型变换器等效电路。n相变换器的n个桥臂通过n个输出端B₁、B₂、…、B_n接出，通过n个电感L₁、L₂、…、L_n接到n相等效电压源负载。和图4-7所示的三相变换器类似，n个等效电压源V_m1～V_mn表征n相负载的平均（基波）电压。O₁和O₂表示的是直流侧和交流侧的中点。

图4-24中，每个桥臂的输出点对直流母线中点O₁的电压都是由PWM决定的切换于正负直流母线电压的脉冲电压序列，因此可以将n相电压型变换器的等效电路简化为图4-25的形式。其中V_B1～V_Bn表示的就是n个桥臂相对O₁的输出脉冲电压。

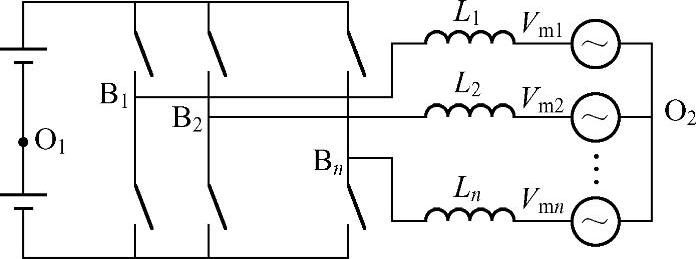
图4-24 n相电压型变换器

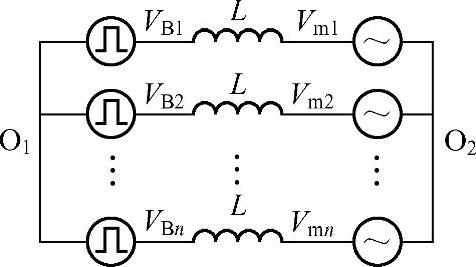
图4-25 n相电压型变换器的等效电路

在图4-25中，抽取任意一相，如第k相（1≤k≤n），得到的电路如图4-26所示。由于交流侧中点O₂与直流侧中点O₁电压并不相同，为了将图4-25的单相回路闭合还需要得到O₂与O₁之间的电压。根据对称性，图4-25的n相支路共模电压就等于O₂和O₁之间的电压，包括n个脉冲电压V_B1～V_Bn的共模电压V_cm以及n个平均电压源V_m1～V_mn的共模电压V_{l_cm}。这样第k相支路就闭合了。由于图4-26中每段电压都可以由n相变换器的占空比得到，这样电感上的电压也能够由占空比得到。这个电路对每个支路都适用，而不需要针对每个开关矢量独立做等效电路的分析。

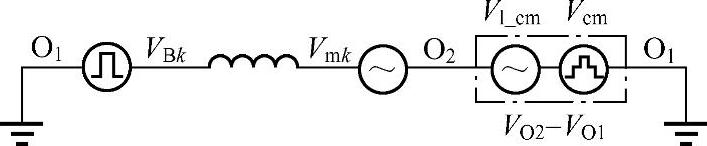
图4-26 n相电压型变换器第k相的等效电路图

图4-26中，每个开关周期内平均电压V_mk和V_{l_cm}都可以视为常量，由占空比决定，而开关电压量V_Bk和V_cm则是阶梯变化量。在一个开关周期内，V_mk等于占空比d_k′与一半直流母线电压的乘积（V_mk=d_k′V_dc/2）。如第2章所述，共模平均电压V_{l_cm}是一个不可忽略的量，等于共模占空比（d′_cm）与一半直流母线电压的乘积。比如对于SVPWM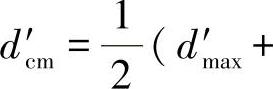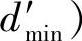，。只有对SPWM此项才为零。图4-27所示为一个开关周期之内的V_Bk和V_cm。图4-27a表示V_Bk在V_dc/2和-V_dc/2之间切换，图4-27b表示在一个开关周期内V_cm有n+1个台阶，每个台阶的电压差为V_dc/n。

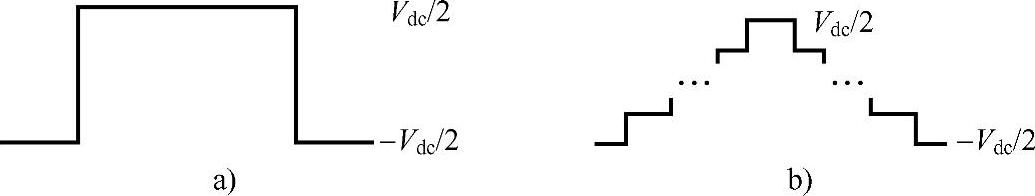
a）逆变器输出电压（V_Bk） b）变换器的端口共模电压（V_cm）

图4-27 第k相等效电路中的开关电压

因此，图4-26中的电压方程可以描述为式（4-14）。在式（4-14）中，（d_k′+d_c′_m）V_dc/2为常数，V_cm是一个2n+2段的电压，如图4-27b所示，前后n+1段对称。其中第m段（0≤m≤n）的电压为式（4-15）。V_Bk是一个三段的两电平电压，如图4-27a所示，在开关周期内可以表示为式（4-16）。为简单起见，定义d″_k=d_k′+d′_cm。

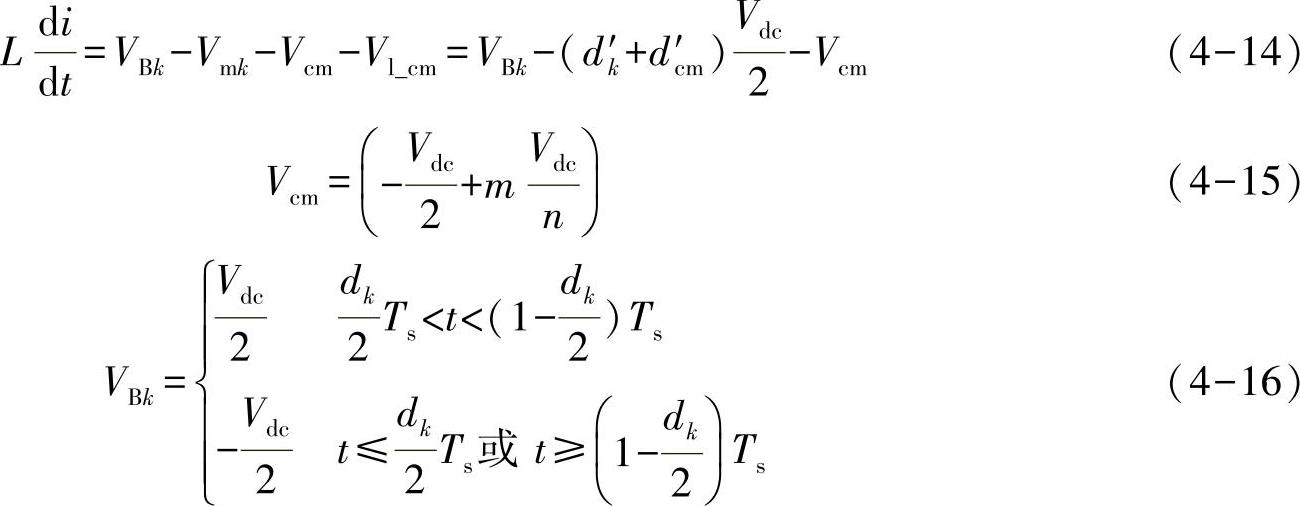
在n相变换器中，每个开关周期可以分为2n+2段，包括中间连续两段，并且前后n+1段对称分布，其电流纹波如图4-28所示。每一段对应一个电压和一段线性的电流纹波。电流纹波斜率由式（4-14）决定。第k段的电流纹波和第（2n+3-k）段是对称的。因此电流纹波的分析可以简化到半个开关周期。

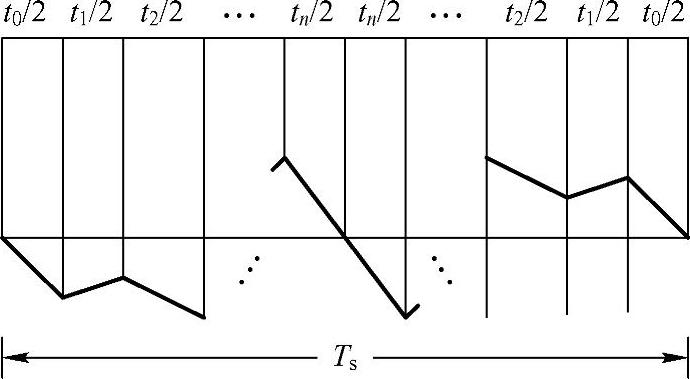
图4-28 n相电压型变换器一个开关周期内的电流纹波

不失一般性，假设占空比大小顺序为d_n≤d_n-1≤…≤d₁。第m相的占空比为d_m。则开关周期中第m段的作用时间由式（4-17）决定，最后第n段的作用时间t_n=d_nT_s，第0段的作用时间为t₀=（1-d₁）T_s。由于脉冲对称性，图4-27中每段时间都要在t_m上除以2。

t_m=d_mT_s-d_m+1T_s （4-17）(www.xing528.com)

根据式（4-15）和式（4-16），在第k相中，第m段的电流纹波变化率由式（4-18）决定，并且可以进一步简化为式（4-19）。

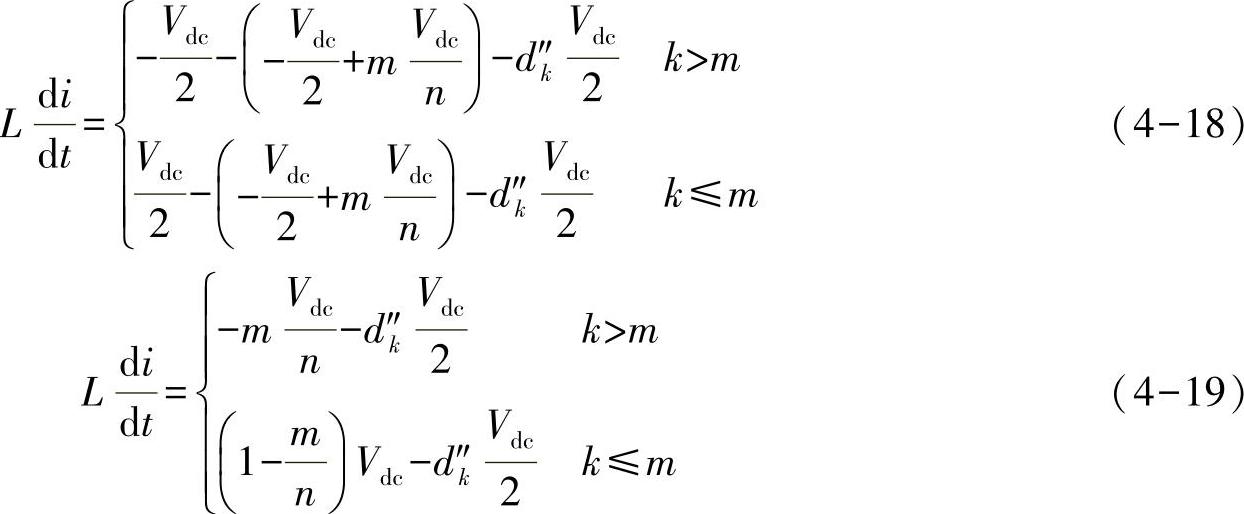
以三相变换器为例，n=3，d₃≤d₂≤d₁。对A相，k=1。在A相的第一段（m=0），Ldi/dt=-d″₁V_dc/2；第二段（m=1），Ldi/dt=（1-1/n-d″₁/2）V_dc=（2/3-d″₁/2）V_dc；第三段（m=2），Ldi/dt=（1-2/n-d″₁/2）V_dc=（1/3-d″₁/2）V_dc；第四段（m=3），Ldi/dt=（1-3/n-d″₁/2）V_dc=-d″₁×V_dc/2。后四段与前四段对称。这样得到的di/dt表达式与4.2节中的结果是一致的。

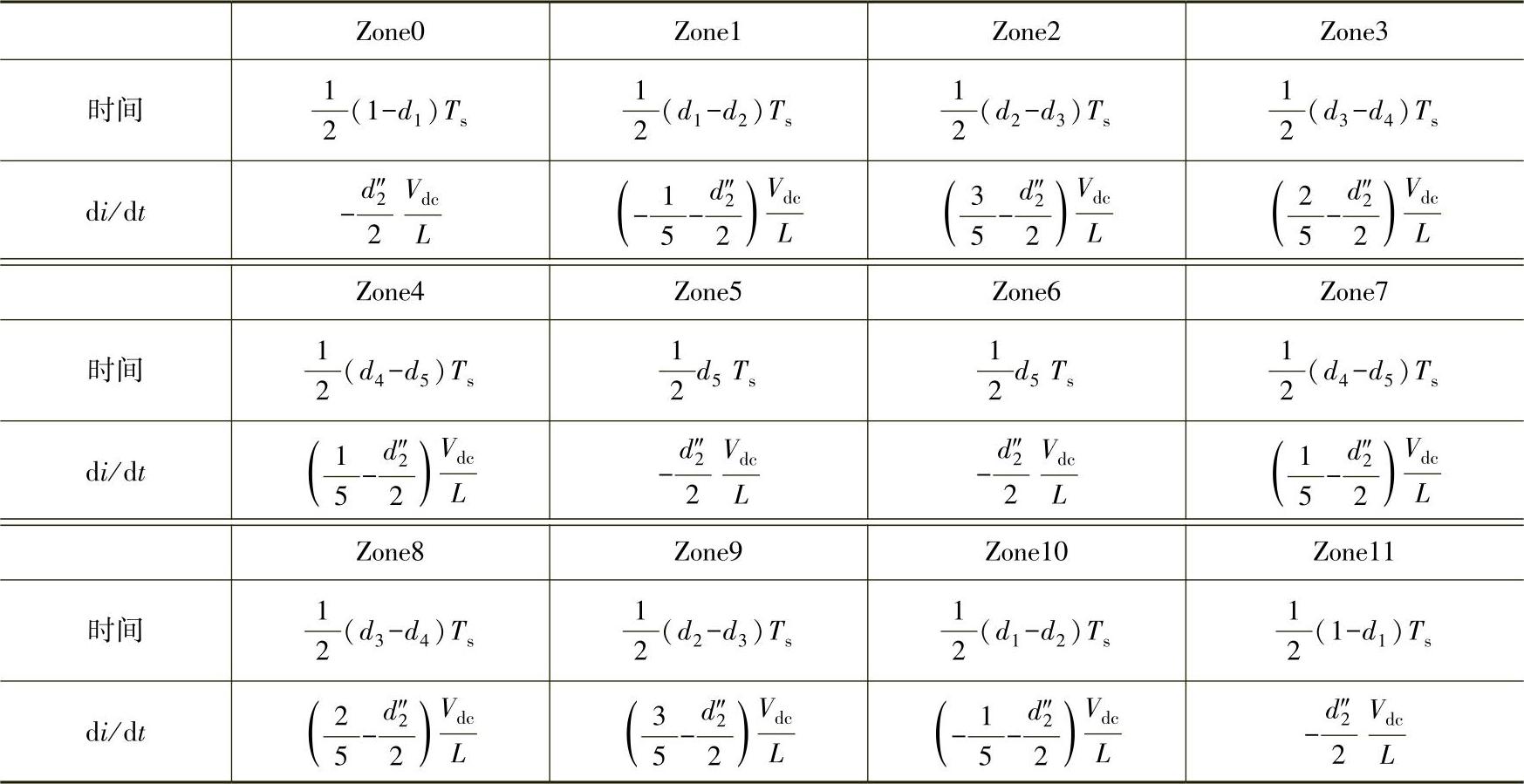
这样的方法很容易推广到多相变换器中。以五相（n=5）变换器为例，每个开关周期有12段直线段的电流纹波。其中第2相（k=2）的电流纹波变化率分析如下：在前半个开关周期内，一共有m=0～5共6段纹波。当m<2时，电流纹波斜率按照式（4-19）中第一个公式，当m≥2时，电流纹波斜率按照式（4-19）中的第二个公式。再考虑到前半开关周期与后半开关周期的对称性，全部12段电流纹波斜率见表4-2。

表4-2 电流纹波变化率的范例：五相变换器的第2相

根据12段电流纹波变化率以及每段的作用时间，即可预测出五相变换器的电流纹波。图4-29展示的是一个典型的五相变换器电流纹波的预测结果，包括一个整基波周期的全图以及局部放大。和三相变换器电流纹波类似，五相变换器的电流纹波分布不均匀。在以T_sV_dc/L为基值的情况下，电流纹波峰值在0.04p.u.和0.06p.u.之间变化。

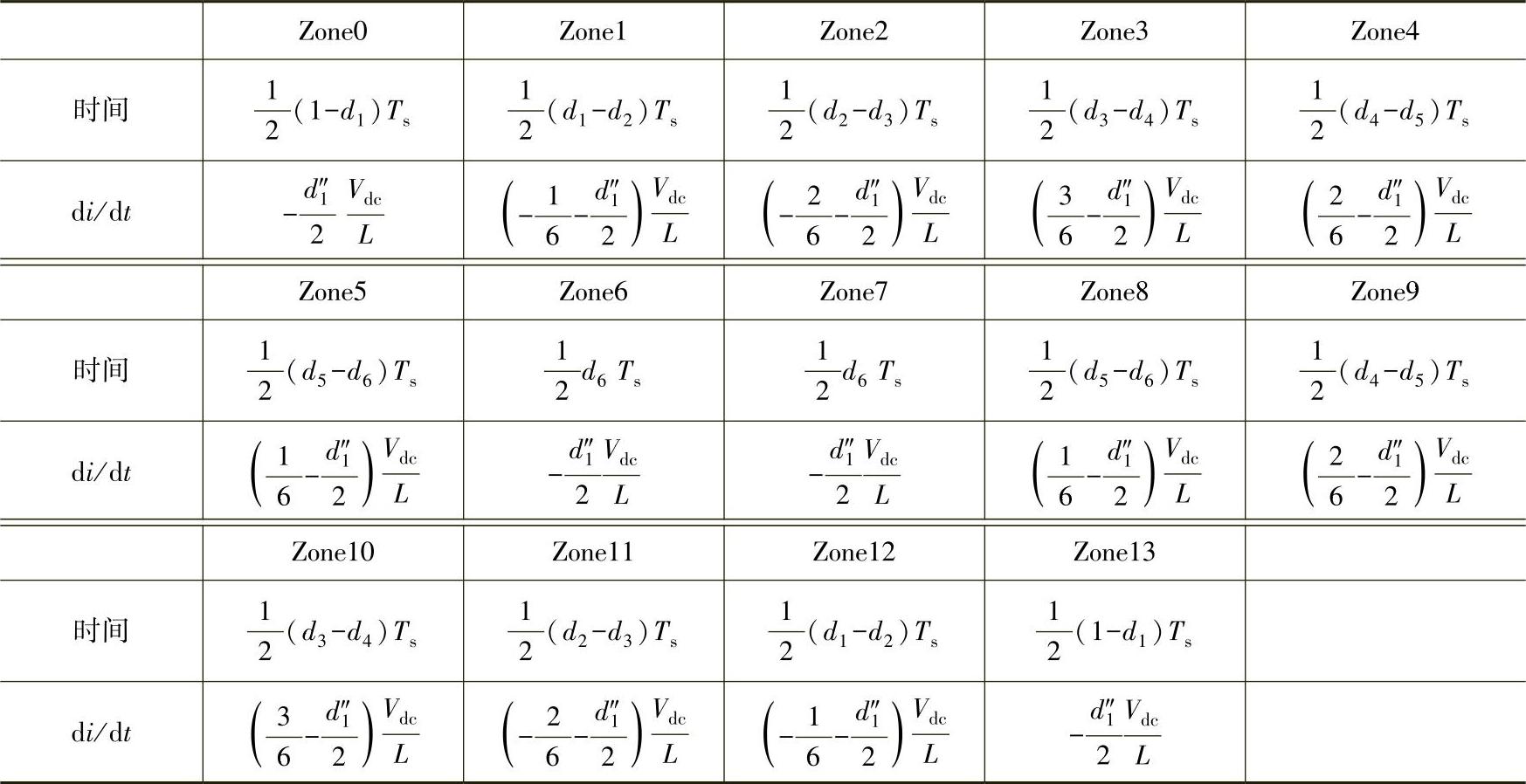
以六相变换器为例，即n=6。考虑其中第3相（d₃）。在式（4-19）中，k=3。每个开关周期有14段电流纹波。在前半开关周期内，m=0～6。m<3时，电流纹波变化率按照式（4-19）的第一个公式，m≥3时，电流纹波变化率按照式（4-19）中的第二式。后半开关周期的7段与前半周期对称，因此可以得到整个开关周期内14段电流纹波变化率的表达式，见表4-3。进而得到六相变换器输出电流纹波预测结果，如图4-30所示。

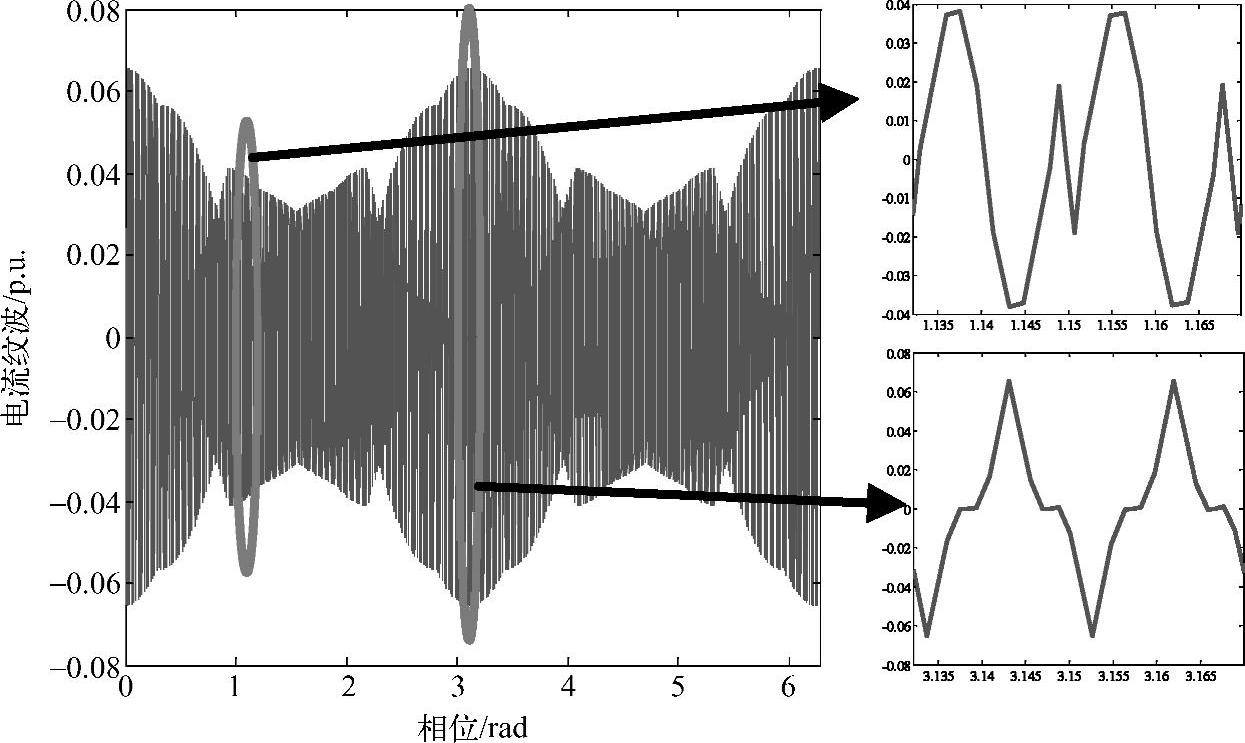
图4-29 五相变换器的电流纹波预测结果：整基波周期和局部放大

表4-3 电流纹波变化率的范例：六相变换器的第3相

同样地，可以将电流纹波预测结果与仿真结果和实验结果进行比较，如图4-31与图4-32所示。图4-31中，对于五相和六相变换器，电流纹波预测峰值和仿真得到的电流纹波的包络线很好地重合在一起。图4-32中，对于五相和六相变换器，电流纹波预测峰值和实验结果的包络线也基本重合。实验中需要考虑到系统的非理想特性，包括电感的非线性等，因此相对误差比仿真结果要大一些。对比结果验证了通用多相变换器电流纹波预测方法的准确性。该电流纹波预测方法相对4.2节中的方法更为简单，尤其适用于多相变换器。

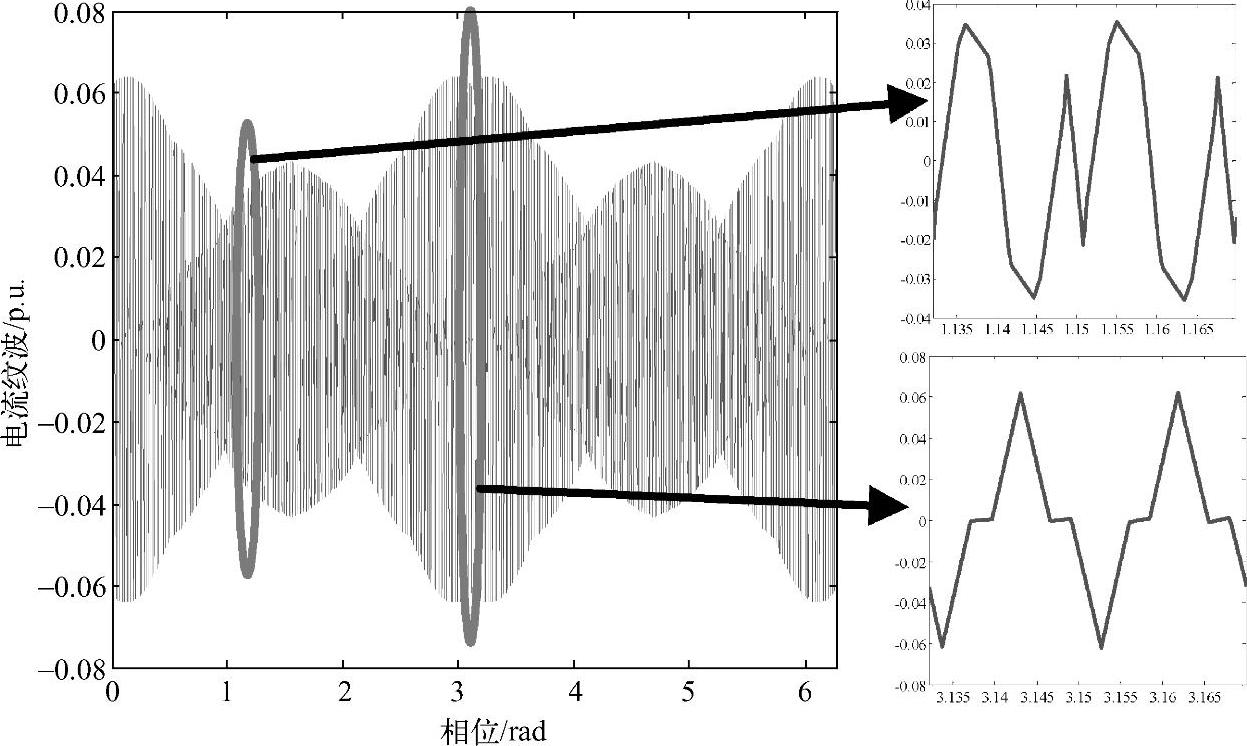
图4-30 六相变换器的电流纹波预测结果：整基波周期和局部放大

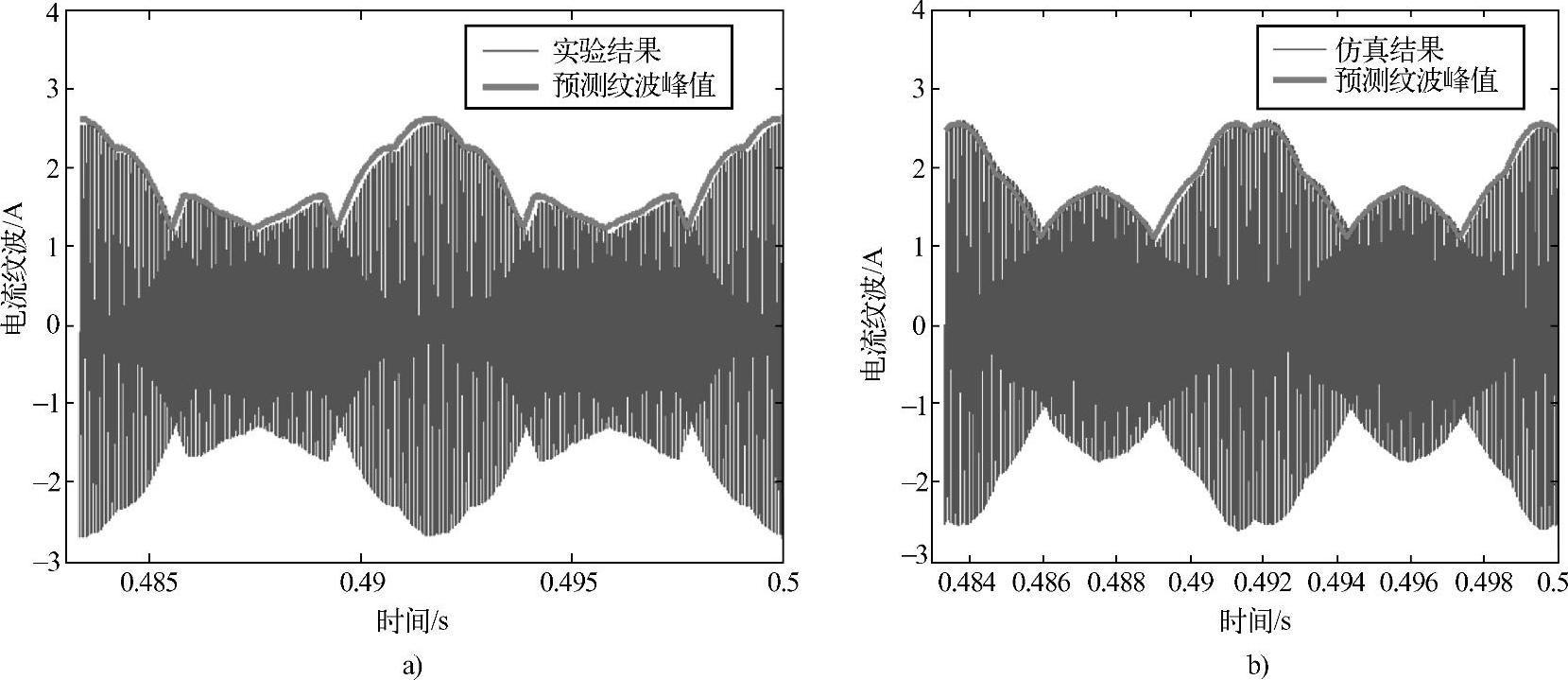
图4-31电流纹波预测结果仿真比较

a）五相变换器 b）六相变换器

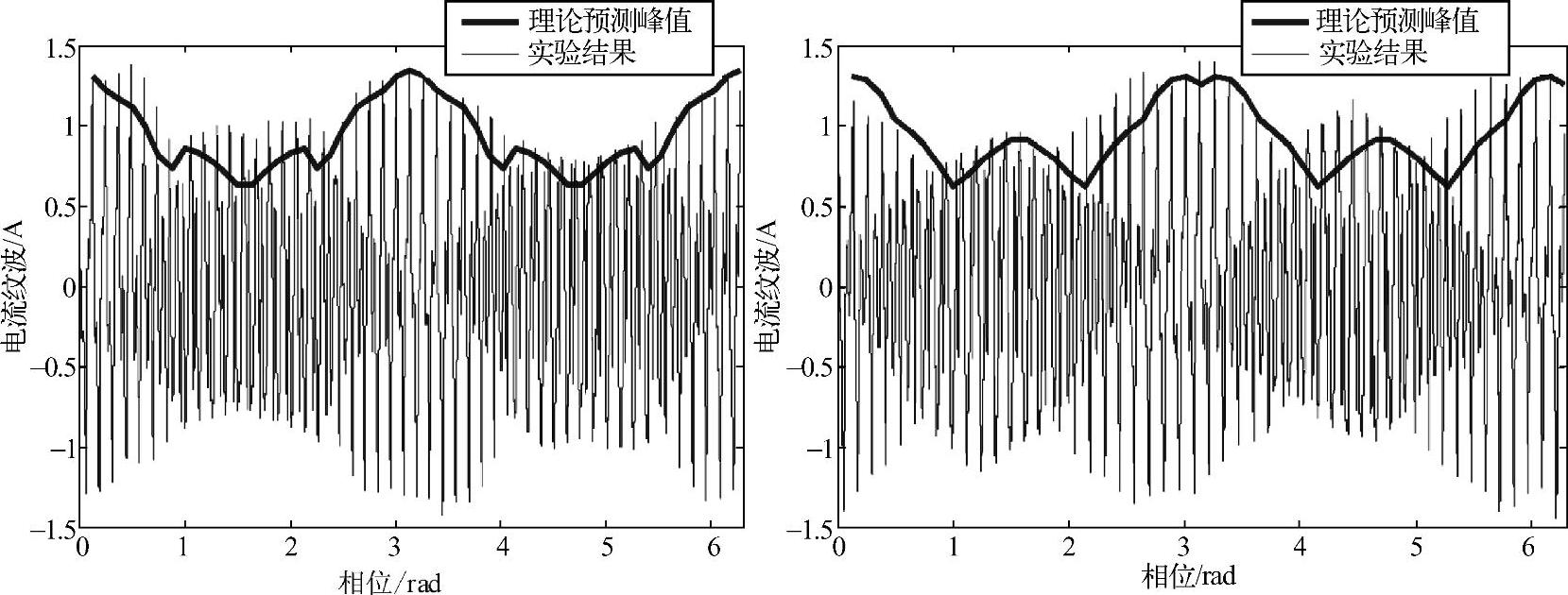
图4-32 电流纹波预测结果实验比较

a）五相变换器 b）六相变换器