三相电压型变换器电流纹波预测——基于戴维南等效电路

和家用单相供电相比，工业应用中普遍采用三相供电，因此三相电力电子变换器在工业应用中更为广泛。图4-7所示是一个典型的三相电压型变换器等效电路。负载用星形联结的三相交流正弦电压源代替，既可表征变频器中负载电动机的反电动势，也可表征并网逆变器中的网侧电压。三相对称电感滤除逆变器高频电压成分，并产生电流纹波。在三相逆变器中，三相占空比为d_a、d_b和d_c，在0～1之间变化。为便于介绍交流电压的调制函数，引入“准占空比”d_x′。d_x′在-1～1之间变化，并且满足d_x′=2d_x-1（x=a，b，c）。在准占空比下，每相输出的平均电压相对于直流母线中点可以表示为

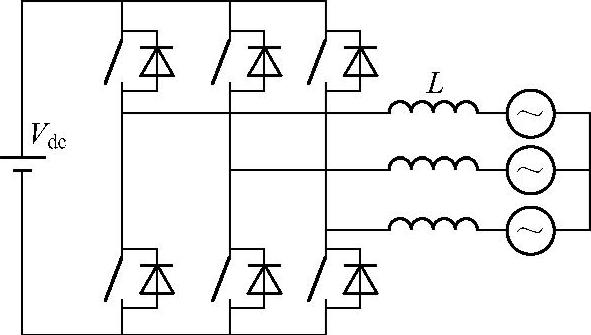
图4-7 三相逆变器与通用交流负载的连接

4.1节中对单相逆变器的电流纹波的分析，可以类似地应用在三相逆变器的电流纹波分析中，即每个电压矢量下，电感两端电压视作固定而电流纹波线性变化。但是和单相逆变器相比，三相逆变器的开关状态要复杂得多。单相逆变器中，单个开关周期只有两种不同的开关状态，而三相逆变器有8种不同的开关状态，三相桥臂中每个桥臂的开关动作都会影响电流纹波。对三相变换器而言，很难推导出如式（4-4）或式（4-6）这样的解析表达式，但是这并不代表三相变换器的电流纹波无法预测。对于8个开关矢量中的任何一个，三相逆变器都对应一个等效电路，通过分析这样的等效电路，可以得到电流纹波的相关信息。图4-8所示是000开关矢量下系统的等效电路，在该矢量下，每个桥臂都通过下管导通接到负母线。如果针对a相进行研究，可以将b、c两相进行戴维南等效，重新与a相一起研究。此时通过单回路的基尔霍夫电压定律，就可以比较简单地得到a相电感上的电压。同时，根据负载电压与变换器输出平均电压平衡的原理，利用式（4-7）代替负载电压，a相电感上电流纹波的变化率可以表示为

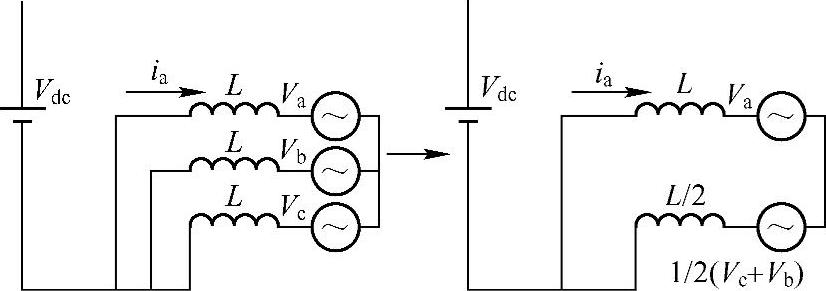
图4-8 矢量000对应的等效电路与其戴维南等效电路

图4-8所示是一个典型的零矢量状态下的等效电路，如果采用非零矢量，如100矢量，对应的等效电路如图4-9所示。a相通过上管导通接入正母线，b、c两相通过下管接入负母线。在研究a相电流时，将b、c相及其与直流母线连接的回路两个端口间的戴维南等效电路与a相支路联立，就得到了单一回路的电路模型，并可以通过基尔霍夫电压定律得到a相电感的电压，并通过式（4-8）得到a相电感的电流变化率，即

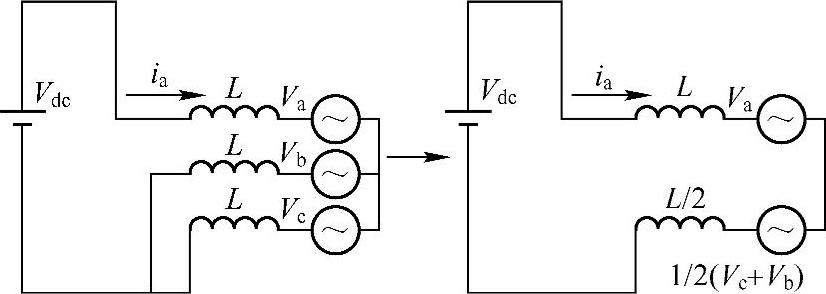
图4-9 矢量100对应的等效电路与其戴维南等效电路

同理，对三相变换器8个电压矢量均做戴维南等效，得到了8组不同的等效电路，如图4-10所示。

综合图4-10所示的8个电压矢量的戴维南等效电路，可得到8个电压矢量中每个矢量对应的电流纹波斜率表达式，见表4-1。

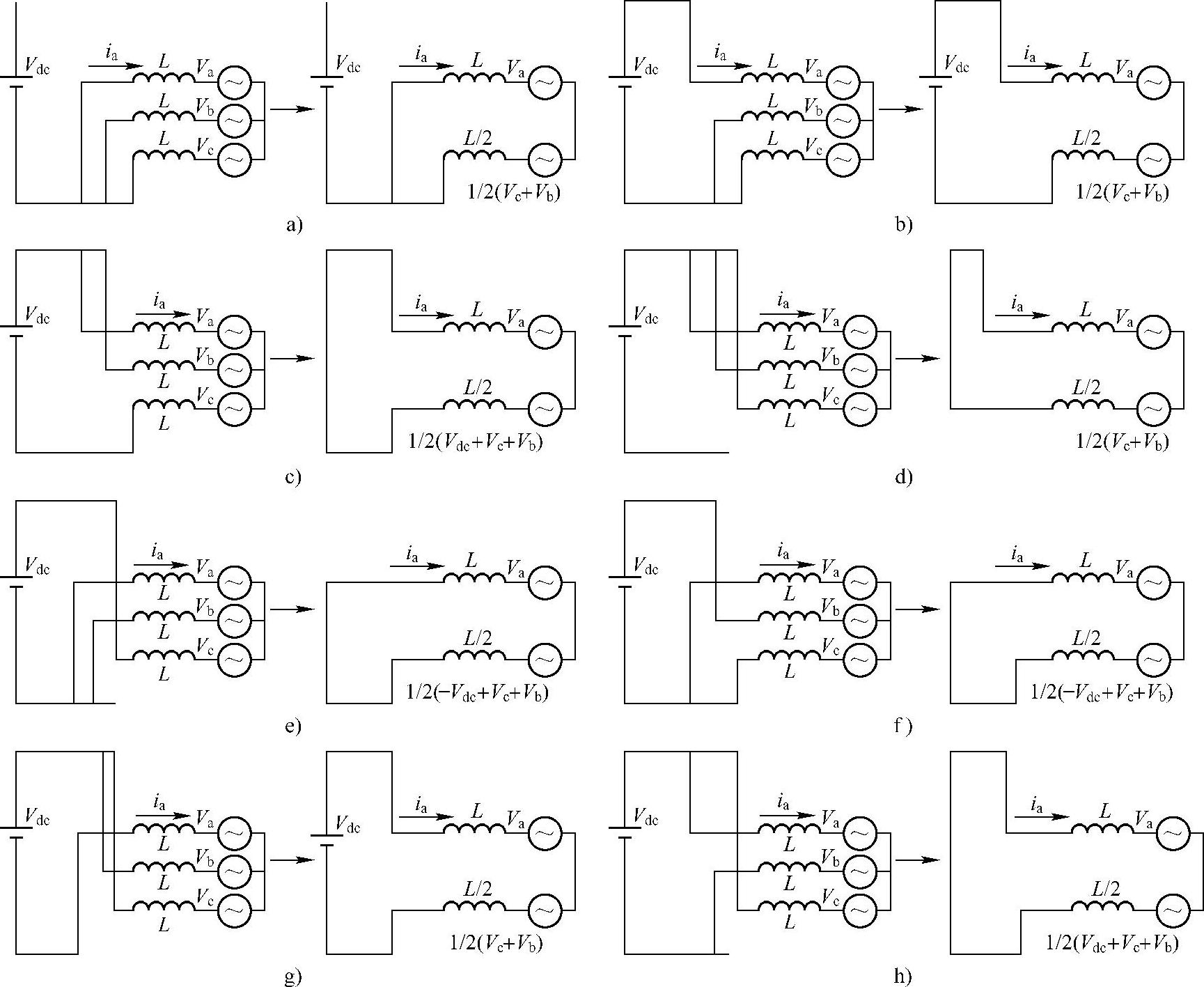
图4-10 8组电压矢量对应的等效电路与其戴维南等效电路

a）矢量000 b）矢量100 c）矢量110 d）矢量111 e）矢量001 f）矢量010 g）矢量011 h）矢量101

表4-1 8个开关矢量及其对应的电流纹波斜率

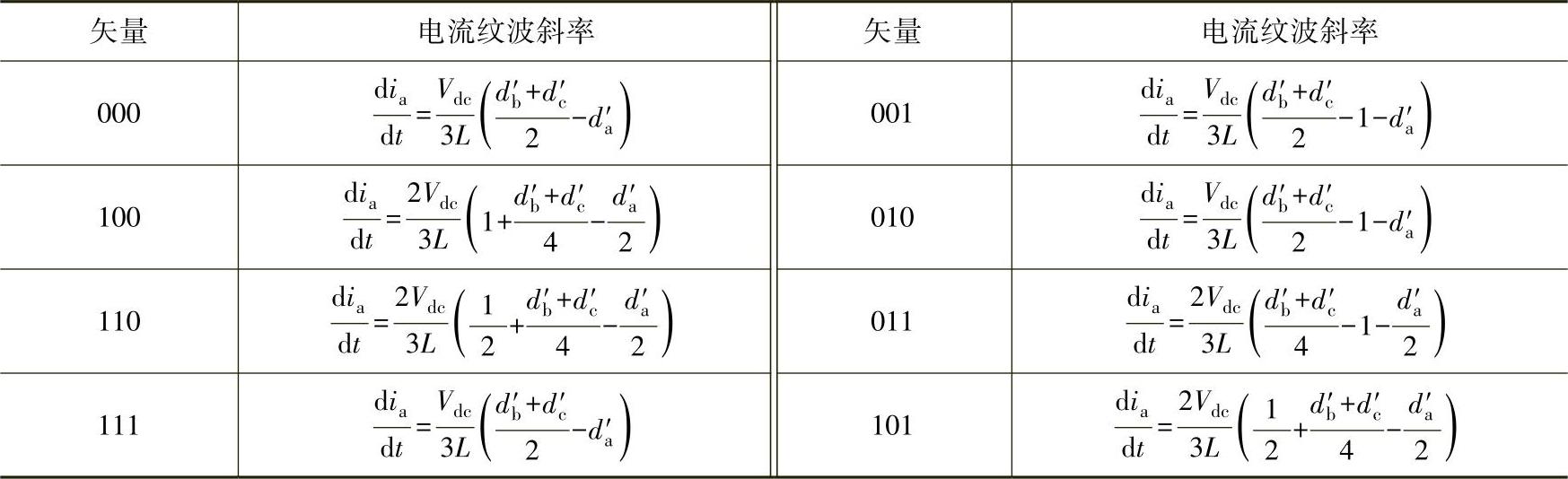
图4-11所示是一个典型的七段式SVPWM单开关周期示意图。在三相变换器中，每个开关周期共具有7段区间。每一段区间对应一个开关矢量，开关矢量作用时间可以由占空比得到；同时，开关矢量所对应的电流纹波斜率可由表4-1得到。即每一段对应电流纹波的时间和斜率都可以由占空比得到。因此，三相逆变器的电流纹波可以预测。

在图4-11的基础上，结合每段电压矢量对应的di/dt和作用时间，可以把七段折线型的电流纹波预测出来，如图4-12所示。以图4-11中的开关矢量顺序为例，在第一段，电压矢量000加载在逆变器上，等效电路如图4-10a所示，根据表4-1中对应的表达式，可以得到a相电流纹波的变化率为k₁。第二段对应矢量为100，在表4-1中也能类似得到a相电流的变化率为k₂，则第一、二段的电流纹波拐点值由式（4-10）得到。根据SVPWM的对称性，最终得到整个开关周期的电流纹波七段式折线，如图4-12所示。根据图4-12的折线形电流纹波，该开关周期内电流纹波的峰值为max（|x|，|y|）。电流纹波的有效值也可以通过图4-12得到，即对应折线型电流纹波的均方根，如式（4-11）所示。

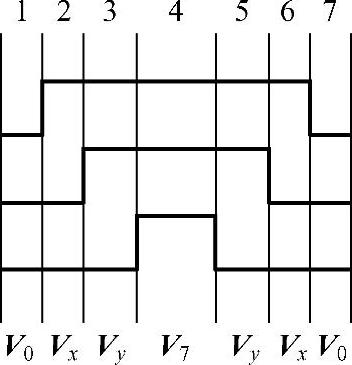
图4-11 典型的七段式SVPWM及每一段对应的电压矢量

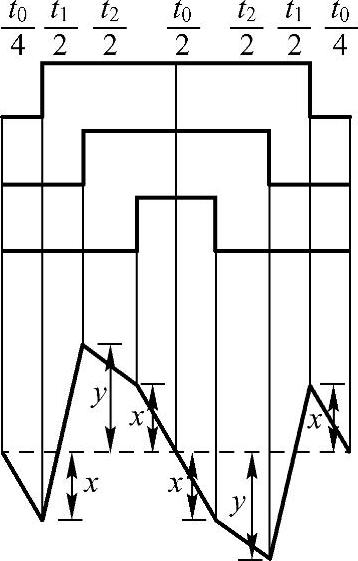
图4-12 典型的七段式SVPWM及对应的电流纹波

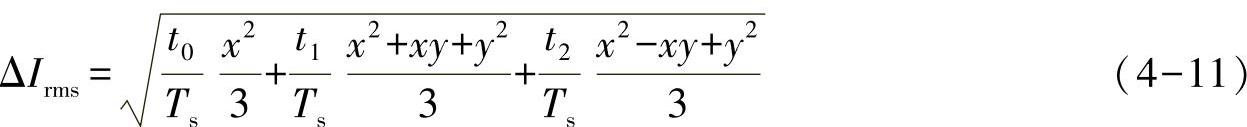
对于五段式DPWM，电流纹波将有所不同。在每个开关周期内电流纹波将呈现五段折线段，每一段对应的电流纹波变化率同样由表4-1得到。根据DPWM中最小脉宽保持为0的DPWMMin和最大脉宽保持为1的DPWMMax这两种不同情况，电流纹波和PWM的示意图如图4-13所示。类似于七段式SVPWM的分析，五段式DPWM的电流纹波的折线拐点也可以由式（4-12）得到。在每个开关周期内，DPWM对应的电流纹波峰值为max（|x|，|y|），而有效值由式（4-13）得到。

(www.xing528.com)

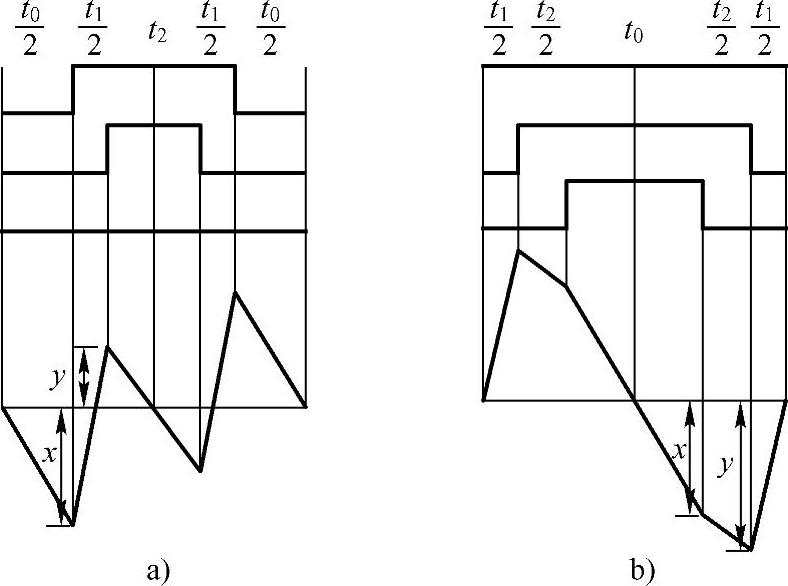
图4-13 典型的五段式DPWM及对应的电流纹波

a）DPWMMin b）DPWMMax

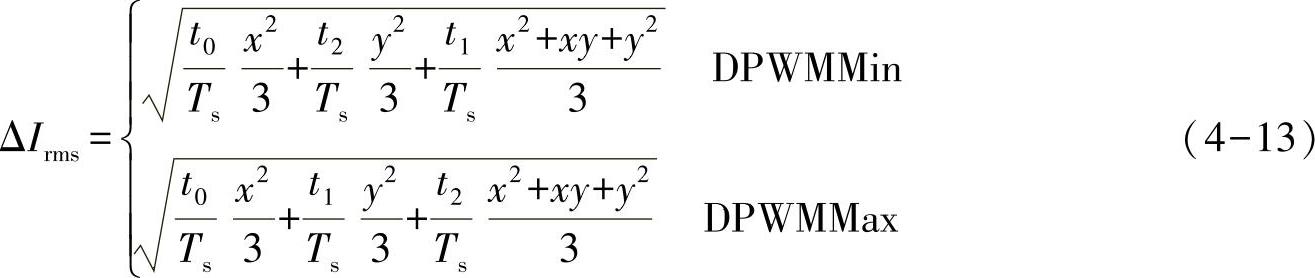
为了验证本节所述的电流纹波预测方法，图4-14～图4-19给出了MATLAB/Simulink仿真波形和理论预测值的对比分析结果。仿真中采用了400V直流母线电压，500μH输出电感，开关频率20kHz和60Hz基波的并网逆变器。图4-14～图4-16采用七段式SVPWM。A相电感电流如图4-14所示，对其进行FFT得到基波幅值相位后，重构得到基波值如图4-14中的粗线所示。将电流仿真结果减去基波值即可得到电流纹波，如图4-15所示。可以看出，不论整体电流纹波（一个线周期内）还是局部的放大比较，仿真结果都和理论预测结果高度一致。如果将理论预测的每个开关周期内电流纹波峰值与仿真结果放在同一张图里，如图4-16所示，电流纹波的预测峰值和仿真结果的包络线重合完好。

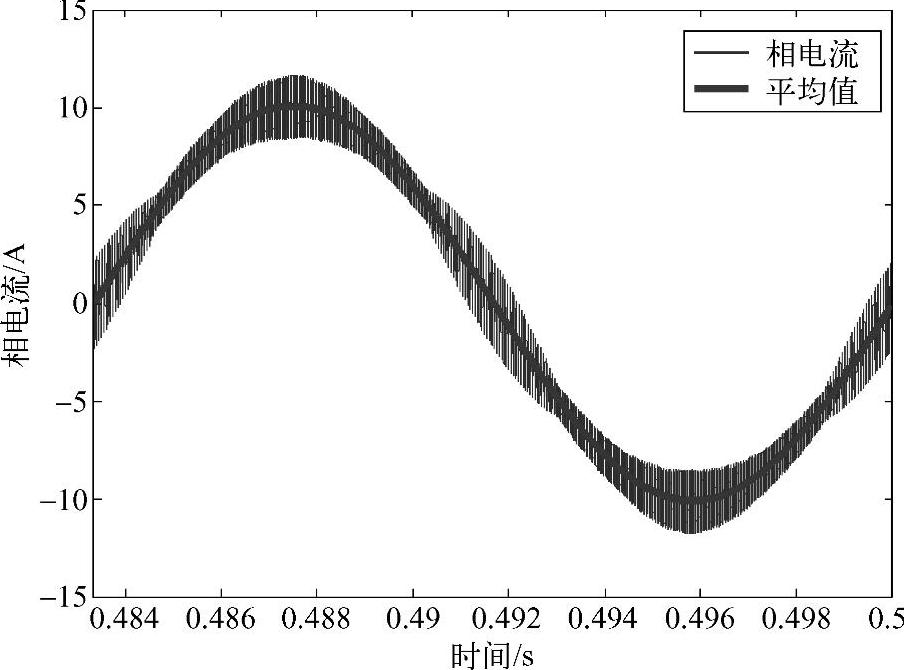
图4-14 仿真结果（SVPWM下的相电流）

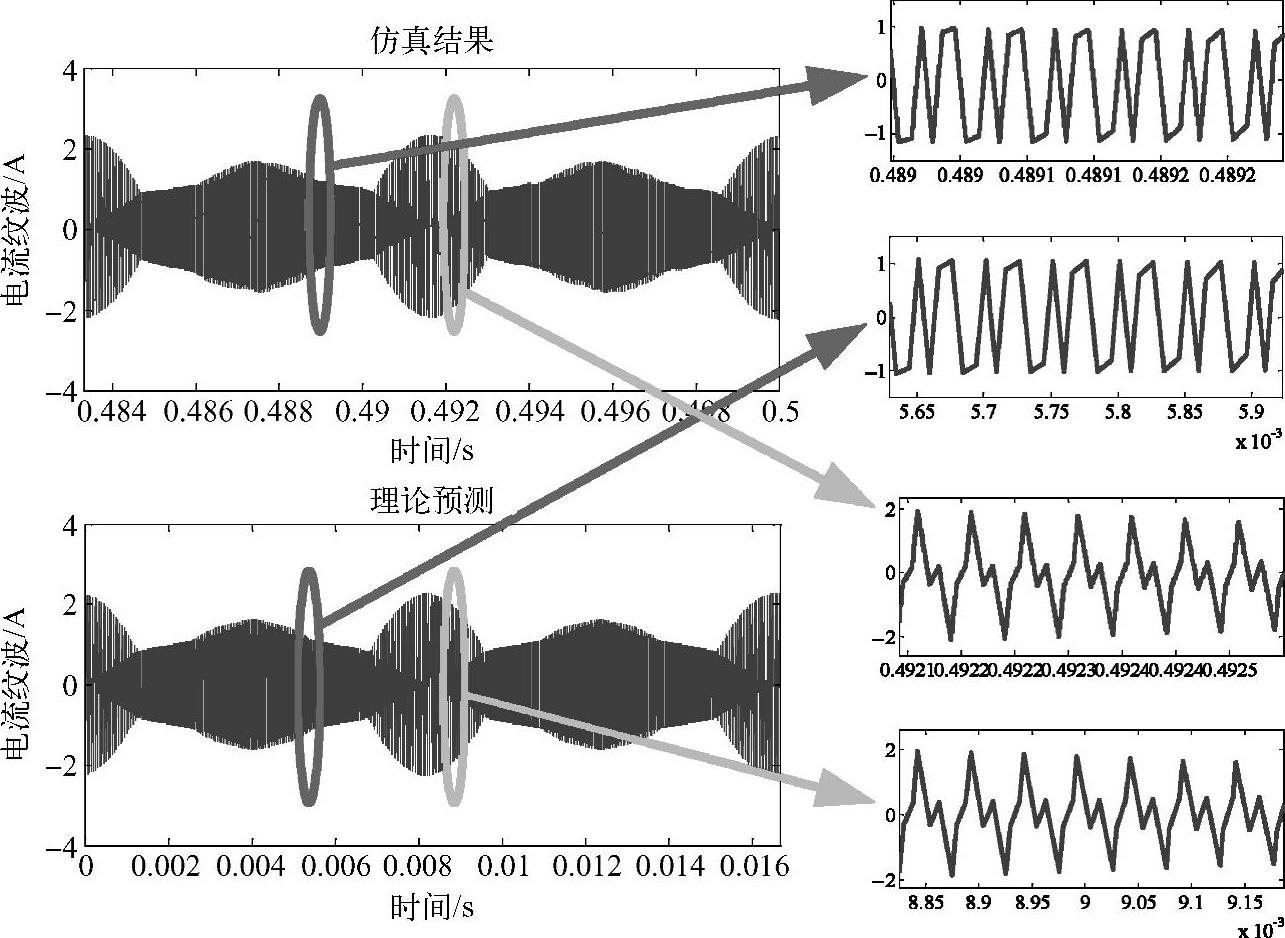
图4-15 电流纹波仿真结果与理论预测的比较（SVPWM）

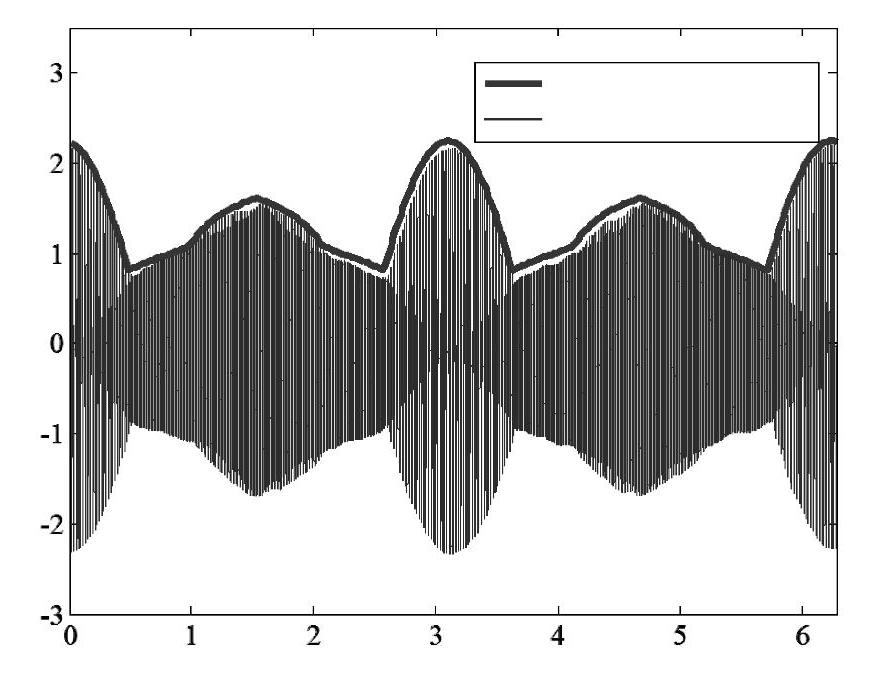
图4-16 电流纹波仿真结果与理论预测峰值的比较（SVPWM）

图4-17～图4-19所示为五段式DPWM仿真理论比较分析的结果。图4-17为DPWM下的相电流波形及其基波（平均）值，相减后得到电流纹波的仿真结果，与预测结果完好吻合，如图4-18所示。图4-19所示是开关周期预测的电流纹波峰值与仿真结果电流纹波的比较结果，可以看出预测的峰值与仿真电流纹波的包络线较好地重合在一起。比较DPWM和SVPWM的电流纹波，可以看出，DPWM的电流纹波峰值要大于同等条件下的SVPWM，这是因为等效开关频率下降了。

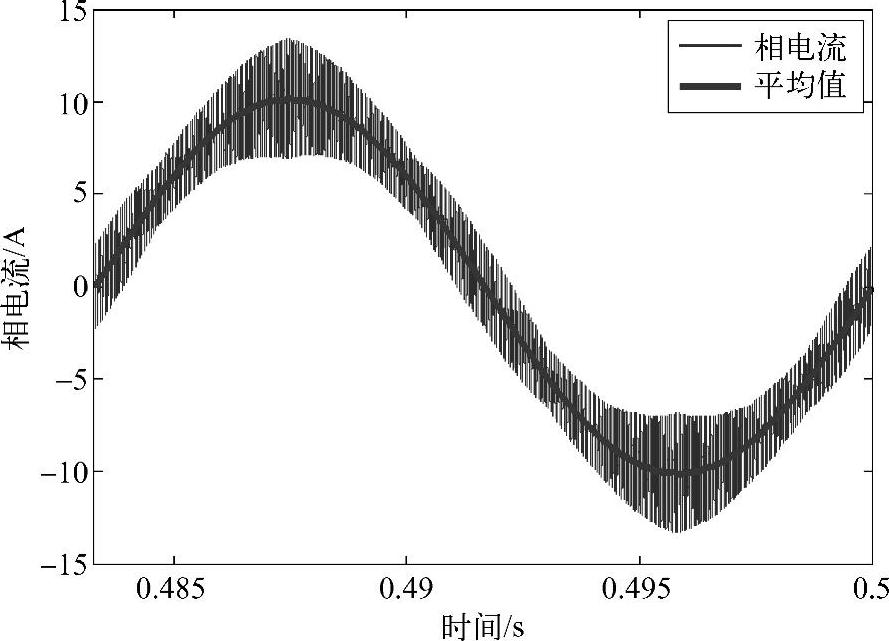
图4-17 仿真结果（DPWM下的相电流）

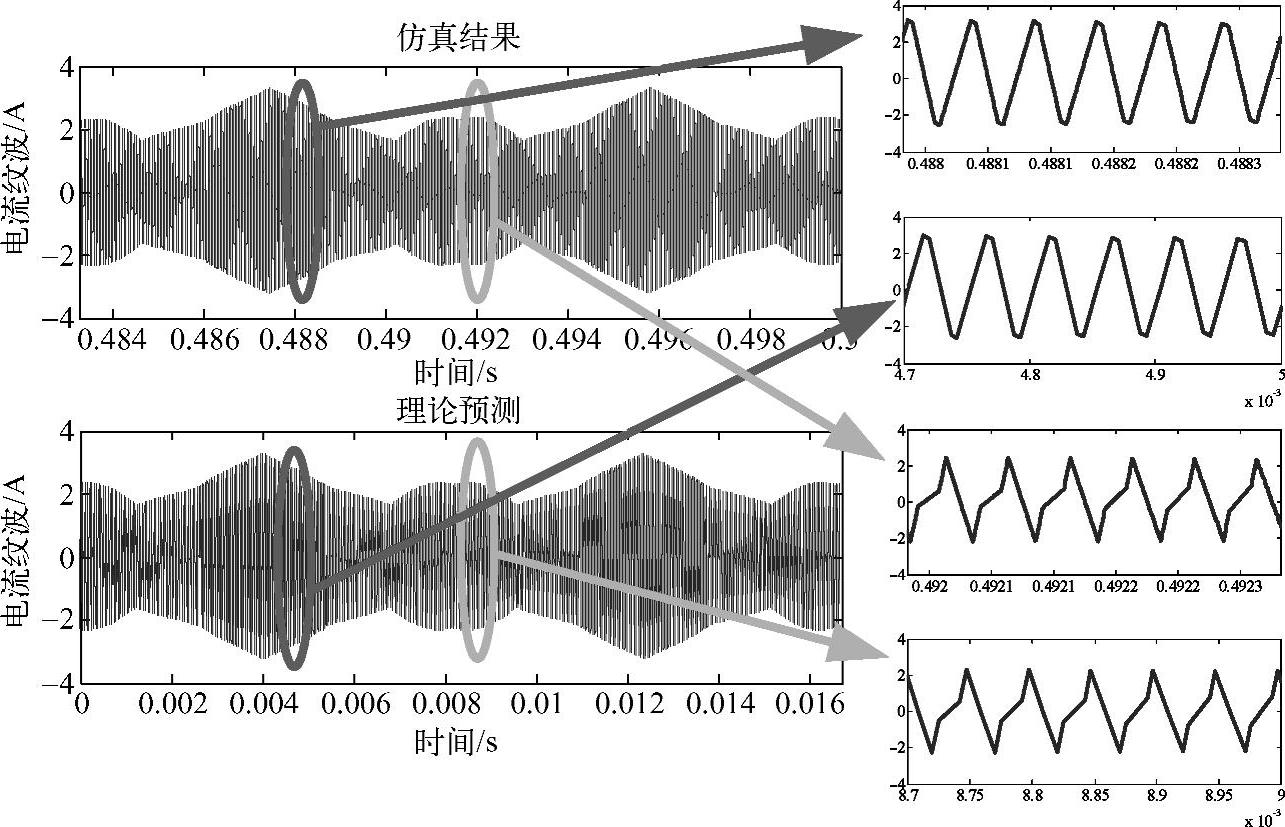
图4-18 电流纹波仿真结果与理论预测的比较（DPWM）

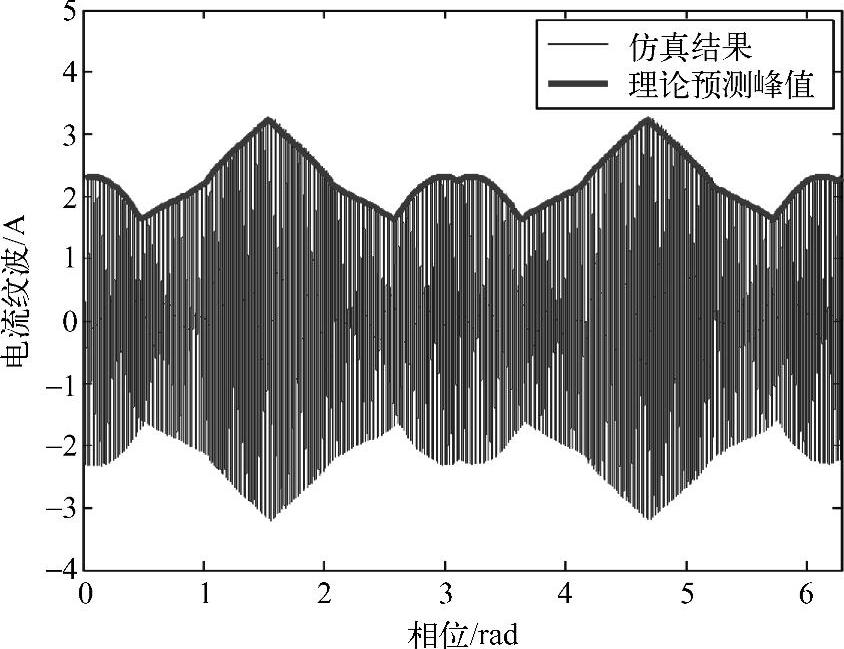
图4-19 电流纹波仿真结果与理论预测峰值的比较（DPWM）

在仿真比较的基础上，进一步进行试验的比较。试验中采用了如下参数：240V直流母线电压，L=800μH，开关频率6.25kHz。采用SVPWM和DPWM的相电流及其基波（平均）值如图4-20和图4-21所示。用实际电流减去基波（平均）电流，得到的纹波电流如图4-22与图4-23所示。可以看出，不论是SVPWM还是DPWM，预测电流纹波峰值和试验结果的电流纹波包络线接近。和仿真结果相比较，试验结果的预测误差要大一些，因为需要考虑试验中包括电感参数变化等非理想情况。

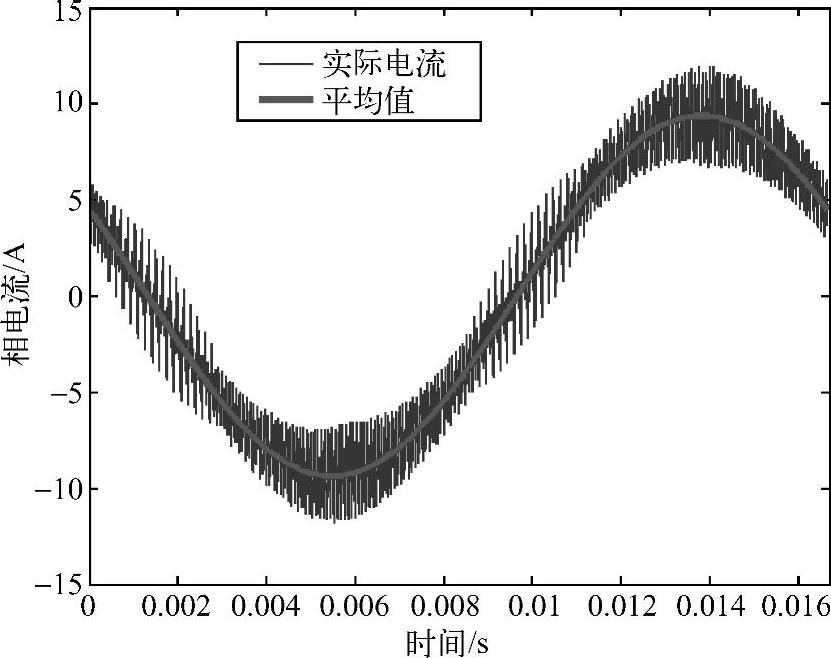
图4-20 试验结果（SVPWM下的相电流）

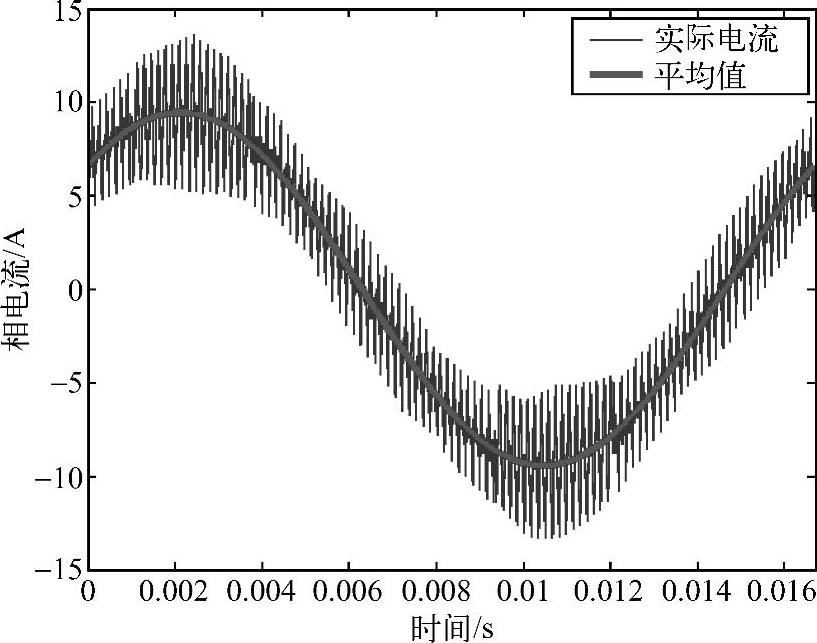
图4-21 试验结果（DPWM下的相电流）

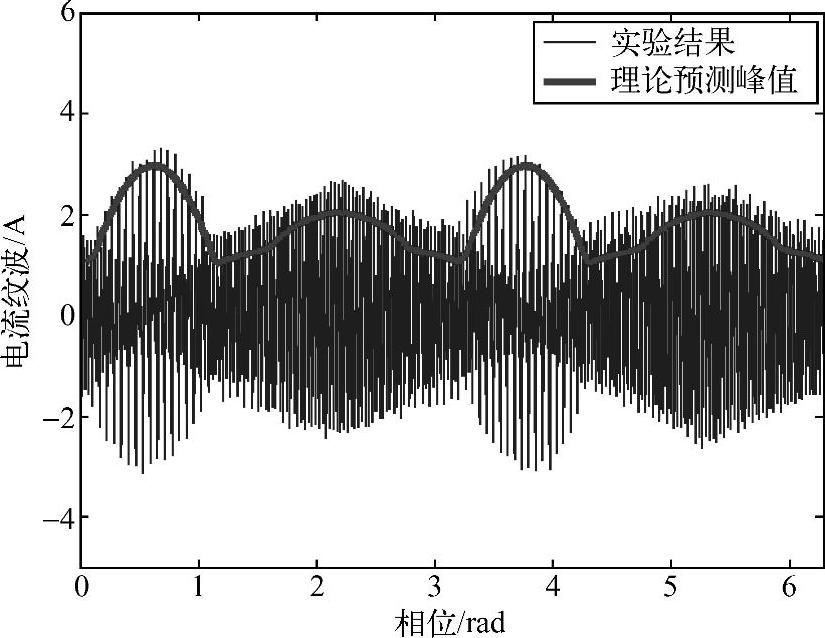
图4-22 试验结果（SVPWM下的电流纹波与预测结果的比较）

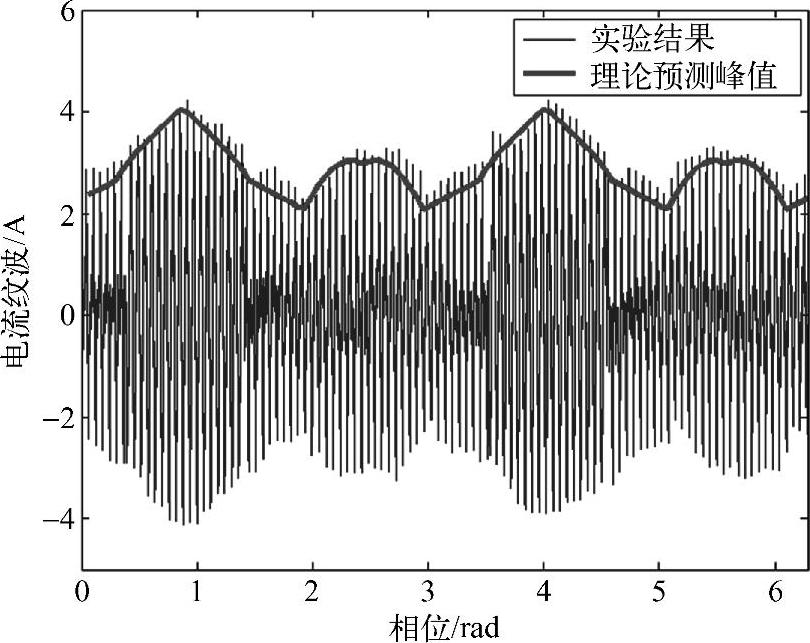
图4-23 试验结果（DPWM下的电流纹波与预测结果的比较）

本节中，利用三相变换器八个开关矢量的戴维南等效电路推导得到了电流纹波的预测方法，并通过仿真和试验比较，验证了预测方法的准确性和有效性。纹波预测方法可以有效地应用在变开关频率PWM的设计中，将在下一章介绍。但是，该方法也有其局限性，4.3节将介绍一种更通用的方法。