预测单相逆变器电流纹波的模型

如第3章所述，电力电子变换器通过对开关器件的通断进行控制，从而实现数字化的电压（流）转换，其端口电压（流）为一系列幅值相等的脉冲，而负载电压（流）呈连续状态。在单个开关周期内，脉冲电压（流）的平均值与负载电压（流）平衡，其瞬时电压（流）差将产生对应的电流（压）纹波。电流（压）纹波通常是评估电力电子变换器性能的一个重要指标，也是PWM的直接控制标准。以较为简单的直流-直流变换器为例，如图4-1所示。针对特定稳态工作点，任意开关周期内开关器件占空比均为定值，电流纹波均保持一致。然而，对于直流-交流以及交流-直流变换器，由于交流侧电压与占空比同步随时间变化，电流纹波也将随时间变化，每个开关周期内并不一致。因此，对于交流-直流以及直流-交流变换器的纹波预测更为复杂；与此同时，也有更多的空间可以加以利用。

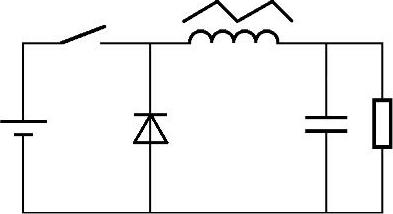
图4-1 典型的直流-直流变换器及电感电流纹波示意图

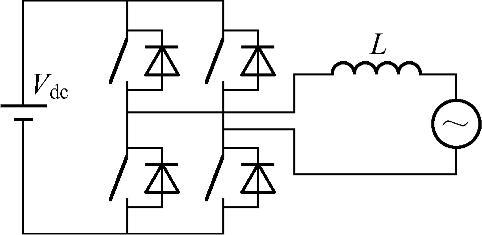
图4-2 典型的单相全桥逆变器结构图

图4-2为单相全桥逆变器拓扑，通过PWM控制，将直流电压逆变成为交流脉冲电压，经滤波电感给交流负载供电。当前，该电路拓扑广泛应用于国内外家用设备供电，比如入户型光伏并网以及插入式混合动力汽车等。针对特定工况，直流母线电压为400V，参考正弦电压频率为50Hz，载波调制比为0.8，PWM开关频率为10kHz。单相逆变器输出负载电流如图4-3所示，实际负载电流由基波电流（平均电流）和电流纹波两部分叠加而成。图4-4给出了一个基波周期内的电流纹波成分，不难发现，单相逆变器的输出电流纹波分布极不均匀，局部电流纹波峰值可达5A左右，而最小电流纹波接近0A。

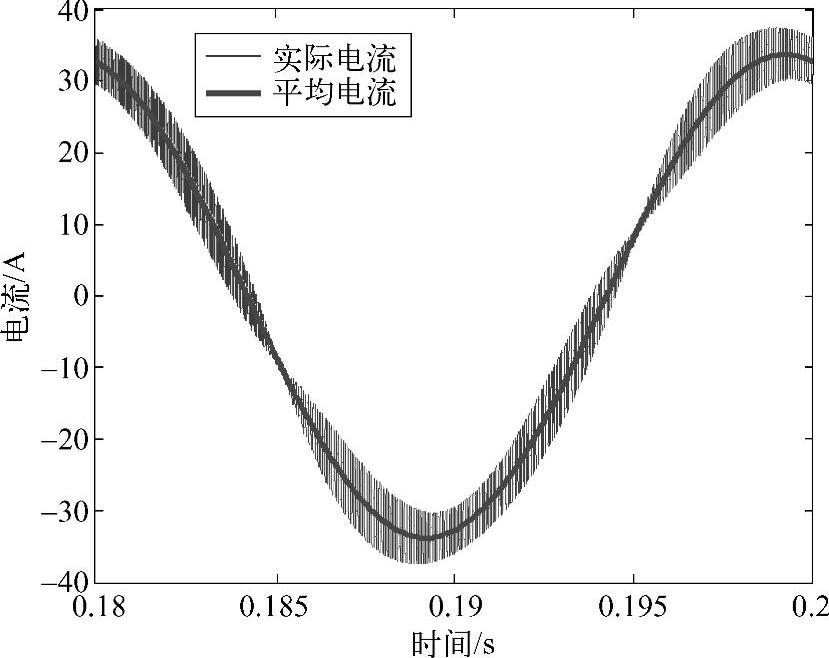
图4-3 单相逆变器输出电流（实际值与平均值）

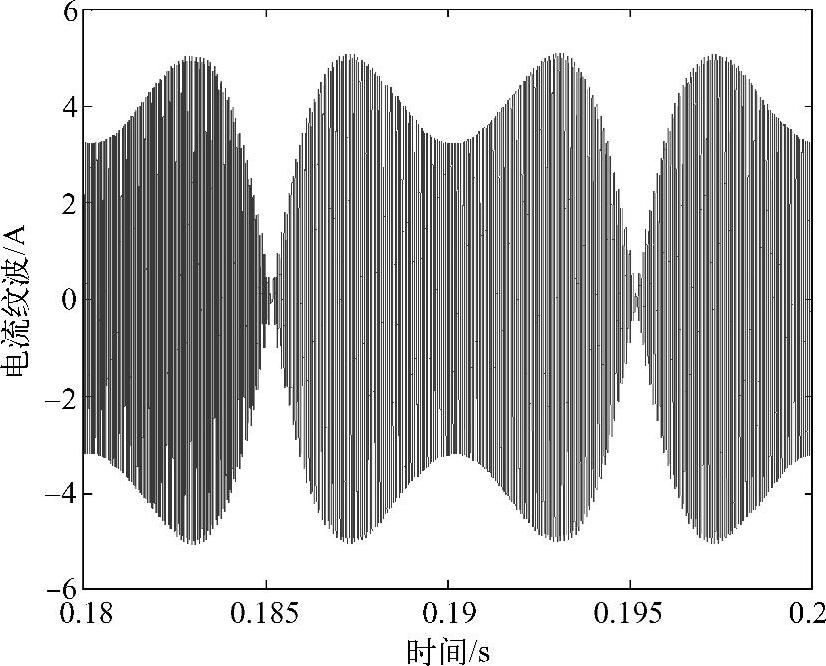
图4-4 单相逆变器的输出电流纹波

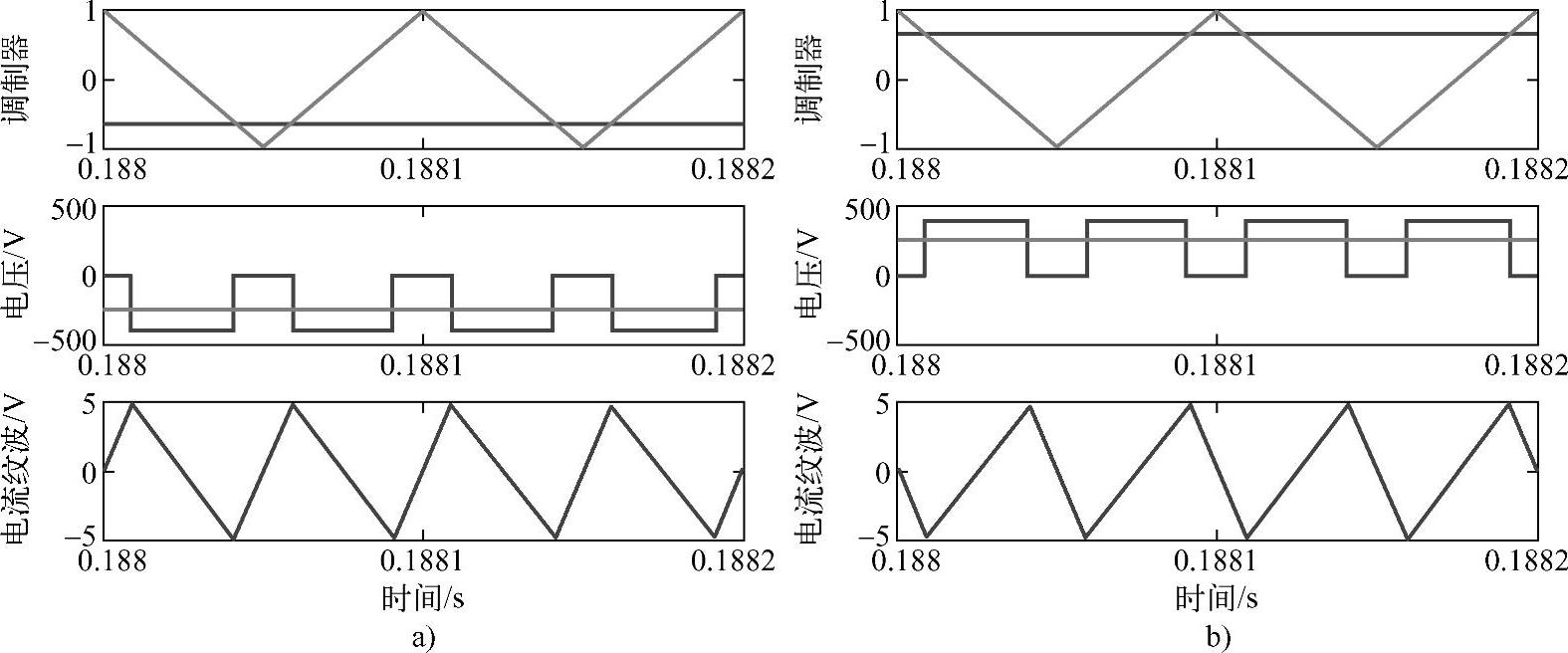
图4-5给出了两个开关周期内参考波-载波、输出电压-输出平均电压和电流纹波示意图，参考波与载波比较生成PWM脉冲信号，通过对开关器件的控制，从而实现输出电压的切换。当参考波处于负半周波时，如图4-5a所示，此时输出电压在负直流母线电压和0电压之间进行切换。在0电压区间，输出电压与平均电压之差为正值，即电感电压降为正值，电感电流线性增加；在负直流母线电压区间，输出电压与平均电压之差为负值，即电感电压降为负值，电感电流线性下降。当参考波处于正半周波时，如图4-5b所示，此时输出电压在正直流母线电压和0电压之间进行切换。在正直流母线电压区间，输出电压与平均电压之差为正值，即电感电压降为正值，电感电流线性增加；在0电压区间，输出电压与平均电压之差为负值，即电感电压降为负值，电感电流线性下降。因此，在单个开关周期内，电流纹波呈现折线状。

在PWM控制过程中，单个开关周期中占空比给定，即各部分电压降作用时间给定，因此电流纹波的线性变化时间可以预先计算；同时，平均电压由参考波决定，即各部分电压降给定，因此电流纹波的斜率di/dt可以预先计算。文献[2]依据这一原则，推导了单相逆变器的电流纹波峰峰值正、负半周波的表达式，如式（4-1）和式（4-2）所示。其中，V_dc为直流母线电压，L为输出电感，T_s为开关频率，d（t）为实时的占空比，其变化范围为-1～1。

(www.xing528.com)

图4-5 单相逆变器电流纹波分析

a）负半周波 b）正半周波

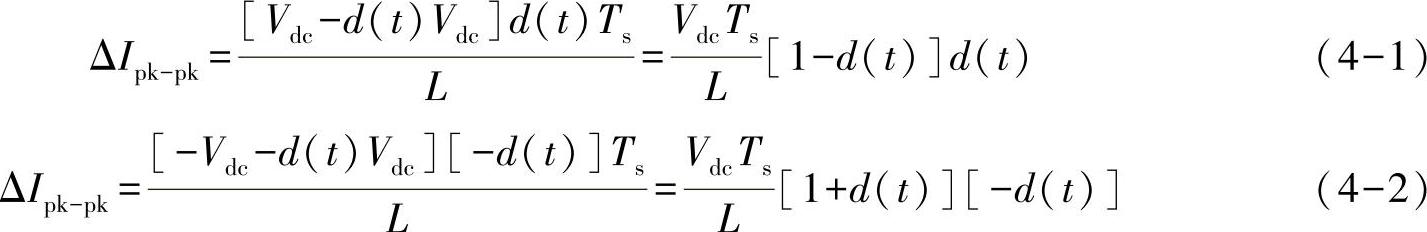
以正弦PWM（SPWM）为例，其占空比d（t）=m_acos（ωt）。其中，m_a为调制比，代入式（4-1）和式（4-2），可得到每个周期的电流纹波峰峰值的统一表达式为

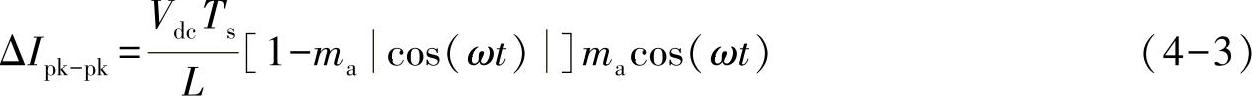
从式（4-3）分析可得，电流纹波分布与相角ωt相关。当相角为π/2时，电流纹波峰峰值达到最小值0；当相角为arccos（0.5m_a）时，电流纹波峰峰值达到最大值V_dcT_s/（4L）。图4-6给出了电流纹波理论计算峰值与仿真结果的比较，可以看出，电流纹波的理论预测值与仿真电流纹波的包络线完全重合，证明了预测方法的正确性。

进一步地，对折线状的电流纹波求均方根可以得到单个开关周期内电流纹波的有效值，如式（4-4）所示。式（4-5）为一个基波周期内电流纹波有效值计算表达式，可化简为式（4-6）。

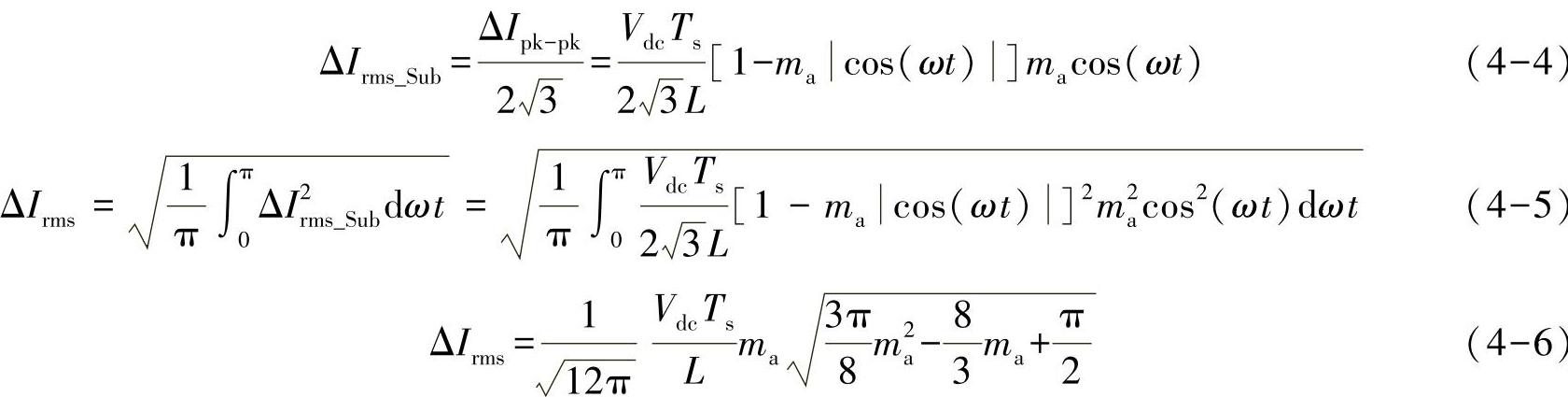
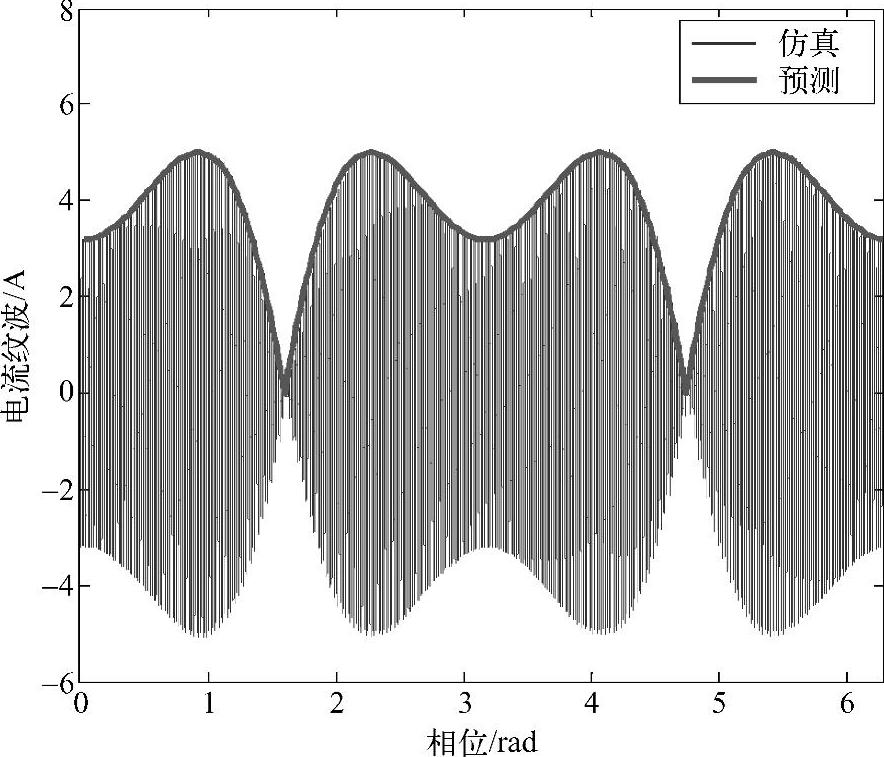
图4-6 仿真与预测电流纹波比较

由式（4-3）和式（4-4）可知，单个开关周期内，电流纹波峰峰值以及有效值和开关频率成反比；同时，单相逆变器的电流纹波在基波周期内分布不均匀。在同样的电流纹波峰峰值或有效值标准下，基于电流纹波的预测模型可实时修改单相逆变器开关频率，从而控制电流纹波峰峰值和有效值在任一开关周期内保持一致。在满足单相逆变器输出电流纹波峰峰值或有效值标准的前提下，可有效降低单相逆变器的平均开关频率，从而降低开关损耗；同时，由于开关频率的变化，系统的电磁干扰不再集中于固定开关频率的整数倍上，这有利于EMI峰值的降低，将在下一章中详细介绍。