PWM的数学分析技巧介绍

PWM是通过脉冲序列的方式逼近连续的参考值，因此必然伴随着不受欢迎的谐波和畸变。在时域上，这些谐波和畸变表现为与正弦连续电压/电流的波形差，但是难以量化描述差别的大小。因此需要通过数学工具来定量评估这些差别。傅里叶变换是实现时域-频域转换的主要数学工具^[2]。

通过对主分量周期为T的电压或者电流波形x（t）进行傅里叶变换，可以得到时域下的级数分解为

x（t）=X₀+X₁cos（ω₁t+φ₁）+X₂cos（2ω₁t+φ₂）+X₃cos（3ω₁t+φ₃）+… （2-18）

式中，ω₁是基波的角频率；X₁和φ₁表示的是基波的幅值和相位，也是需要通过PWM实现的目标值。其他分量就是不希望得到的谐波值，包括直流分量X₀和高次谐波X₂、X₃等。

输出电（压/流）有正有负，但是由于负载的主要功率损耗都表现为欧姆损耗，在评估谐波性能时，有效值是一个重要的参数。通过对时域波形求方均根可得到时域波形的有效值。如果对式（2-18）两侧在一个基波周期内求方均根，由于傅里叶级数的正交性，不同频率分量之间的有效值为零，因此得到的有效值表达式为

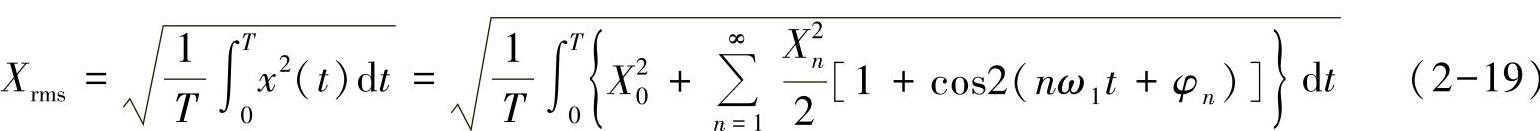
由于积分项中含余弦函数的部分在整个周期的积分值为零，因此通过式（2-19）得到的有效值的表达式可简化为式（2-20）。即时域波形的有效值二次方等于各频率有效值的二次方和。

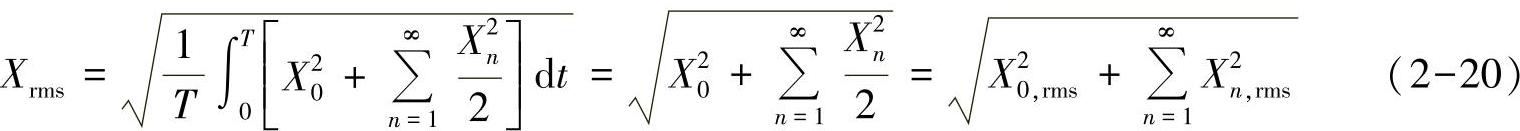
大多数情况下，期望的输出是基波分量X₁，其余部分作为谐波畸变量，可以将式（2-20）改写为

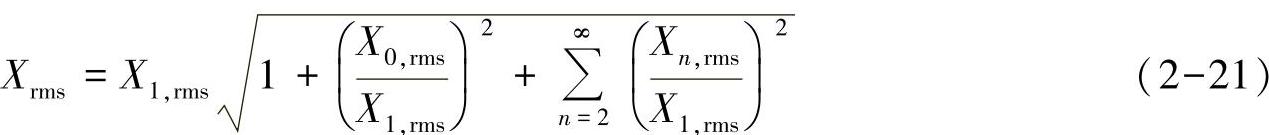
于是可以定义总谐波畸变率（THD）如式（2-22）所示，即各次谐波与直流分量相对基波分量的二次方和之二次方根，表征的是除基波分量的其他量的畸变程度。

如上定义的THD中，X可以是电流也可以是电压。当X是电流时，THD的物理意义更为明确，因为电阻损耗都是和各次谐波电流的二次方成正比的，THD的二次方正比于各次谐波的二次方和，代表了谐波电流造成的电阻损耗的趋势。而当X是电压时，其代表的物理意义不再是电阻损耗的趋势。由于电机等典型的负载都是电感特性的，因此阻抗与频率成正比，在各次谐波电压下，对应的谐波阻抗与谐波次数成正比。对应这种情况，还有一种加权的总谐波畸变率，如式（2-23）所示。首先认为直流分量为零，每次谐波求二次方和的时候还需要除以对应的谐波次数n再求二次方。这样，权重系数1/n就能反映阻抗随频率正比增加的影响了。图2-26所示是感性负载下PWM逆变器输出的电压和电流波形以及不同频率下的电压谐波、电压加权谐波和电流谐波（均为标幺值）。可以看出，电压谐波远高于电流谐波，而电压加权谐波基本接近电流谐波的值。电压THD为1.21，电压加权THD为0.023，而电流的THD为0.025。

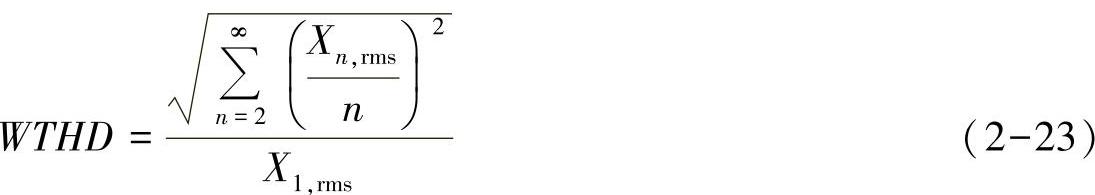
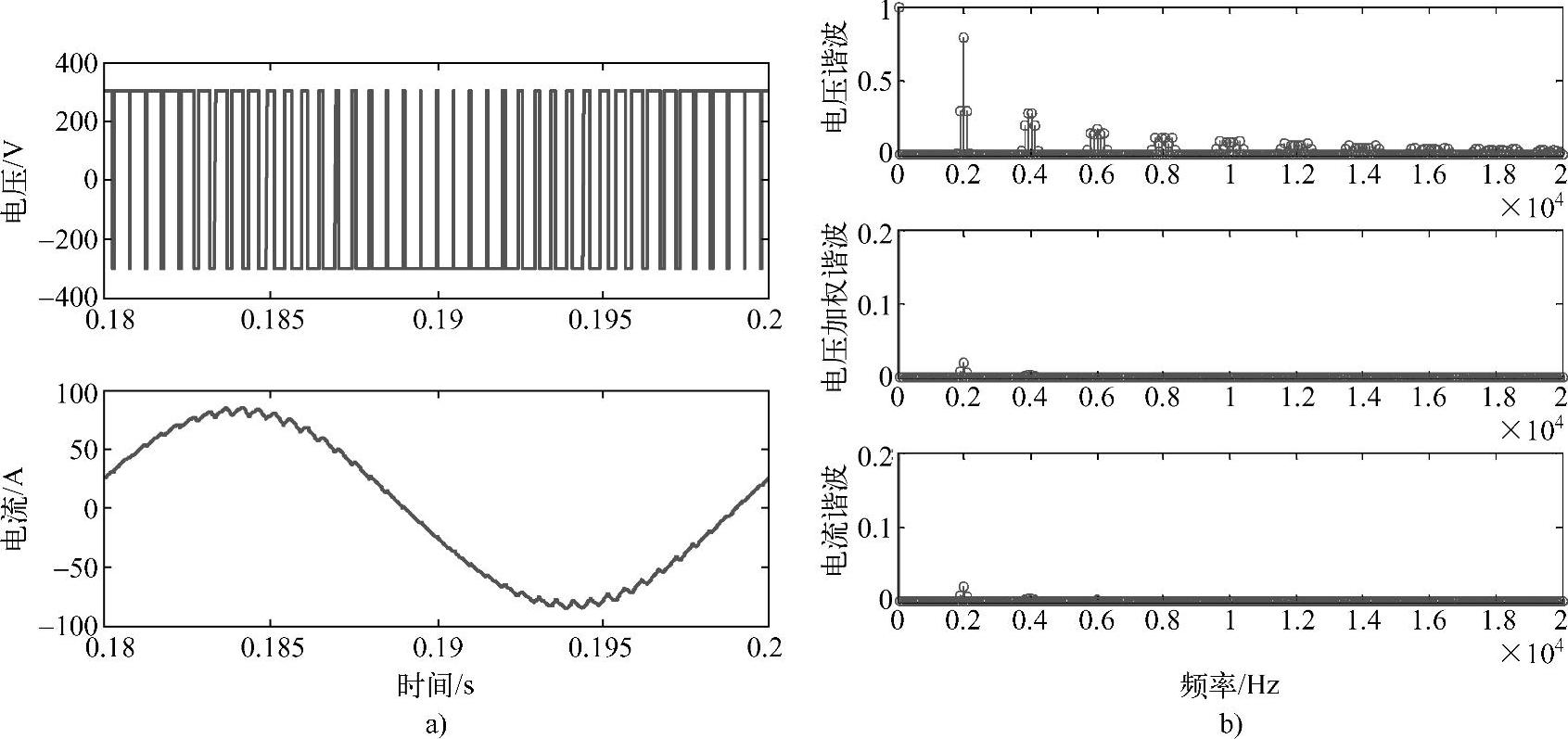
图2-26 PWM逆变器的输出电压及电流(www.xing528.com)

a）时域波形 b）谐波频谱

另外，不同负载对于谐波的阻抗和损耗等也有不同的影响，比如感应电机中转子电阻、转子漏感随频率的变化以及铜损随频率的变化，都能够影响谐波加权系数，综合考虑这些因素得到的加权系数远比式（2-22）复杂。评估谐波的影响还需要针对负载进行^[2]。

以上的数学分析都是通过傅里叶变换实现的。傅里叶变换被称作“信号处理的眼睛”，可以对任意时域波形进行分析，得到频域的对应结果。快速傅里叶变换（FFT）算法被发明以来，基于傅里叶变换的信号分析和处理得到了广泛的应用，但是傅里叶变换在分析高载波频率的PWM系统时面临计算量和分析精度的矛盾，并且难以以较为简单的数学表达式描述各次频率分量。正是因为这些原因，基于解析表达式的双傅里叶变换（二重傅里叶变换）在PWM系统的分析中得到了应用，在很多场合能够得到比FFT方法更好的效果^[2]。

PWM系统的一个主要特点是系统包含了基波和载波两个频率分量的信息。这两组频率分量相对独立，可以假设为

式中，ω_c和θ_c为载波的角频率和相位；ω₀和θ₀为基波的角频率和相位。

对于一个时域信号f（t），可以描述为x和y的二维函数f（x，y）。这样，可以通过类似傅里叶分析的方法得到

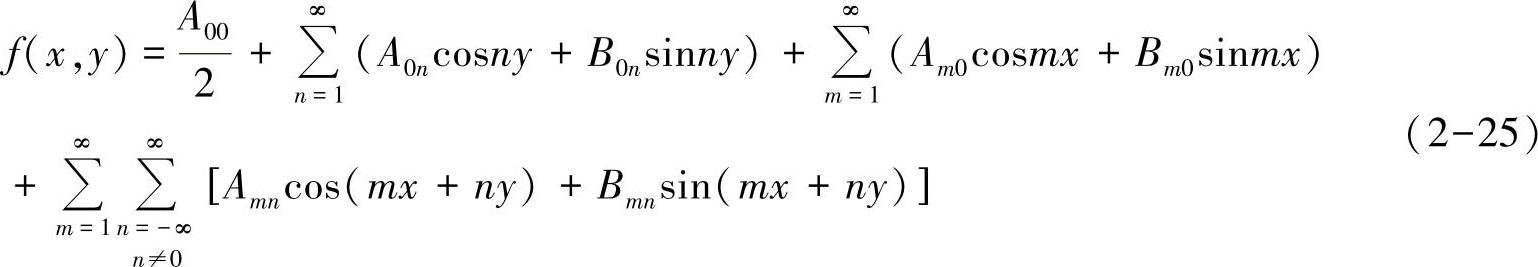
其中双傅里叶系数由式（2-26）得到，即

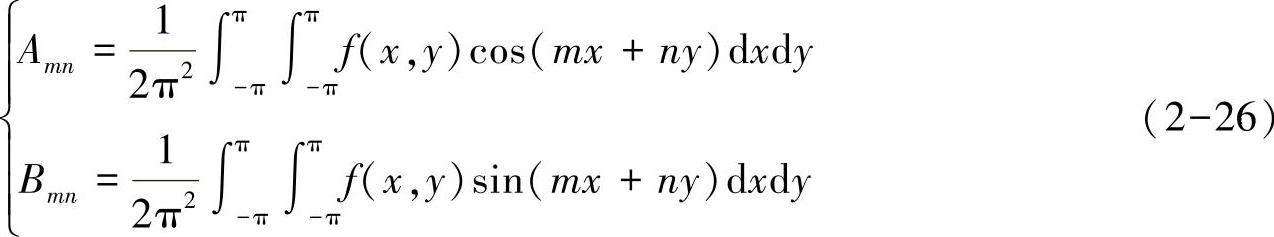
将式（2-24）代入式（2-25）得

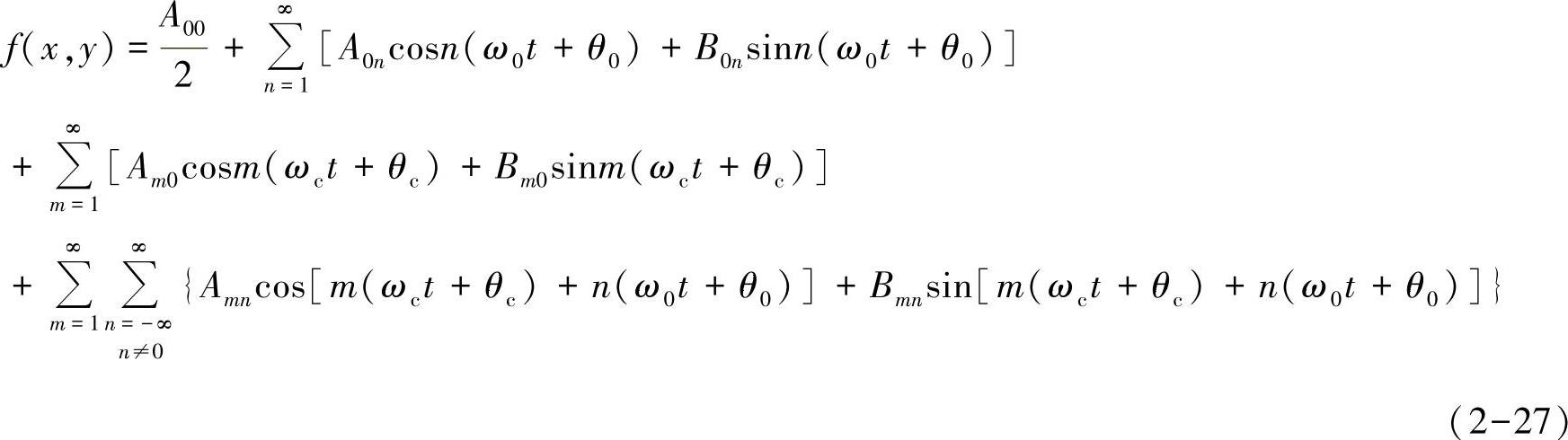
式（2-26）中右侧的第一项是直流偏置分量，第二项为基波分量，第三项为开关频率谐波分量，第四项则是包括了各次开关频率及其加减若干次基波频率的边带分量。通过式（2-27）就能用解析的方法描述关注的各个频率的分量了，有关双傅里叶变换的方法在本章文献[2]中有详细的介绍，本节不再详细描述。

不论是基本的傅里叶变换还是双傅里叶变换，都是纯粹的时域-频域变换。它们都存在时域-频域变换中的一些明显不足。首先，缺乏时间和频率定位的功能：对于给定的信号，傅里叶变换无法得到某一特定时刻该信号对应的频率是多少，也无法通过频域结果反推该频率信号对应的发生时间，这种缺陷给PWM应用中的开关频率变量带来了很多局限；其次，傅里叶变换对于非平稳信号存在局限性，傅里叶变换的对象都是假定信号频率不随时间变化的，对于PWM中频率分量随时间变化的情况以及暂态过程都缺乏良好的分析能力；第三，傅里叶变换在分辨率上也存在局限性。这三大局限性都制约了傅里叶变换对PWM系统的分析能力。为了改善这种分析能力，近年来在PWM的分析中还引入了包括短时傅里叶变换和小波变换在内的时频联合分析方法。限于篇幅，本节不再过多介绍[9]。