空间矢量PWM与载波比较PWM的关系探析

本章介绍了空间矢量合成和载波比较这两种典型的PWM实现方式。事实上，对变换器本身，在任意工作状况下物理上实现PWM只是通过唯一确定的门极驱动信号实现的，并没有空间矢量合成或者载波比较生成的区别。因此，物理上空间矢量PWM和载波比较PWM应该是统一的。本节的内容就是建立这两种PWM方式的关系。

首先，由于空间矢量PWM认为在一个开关周期内参考电压矢量是固定不变的，能用相邻矢量合成参考矢量并用零矢量补充剩余开关周期的时间，所以空间矢量PWM对应的是规则采样的载波比较PWM，即开关周期内三相参考值为常数。

图2-4所示为七段式SVPWM及七段对应的矢量：以第一扇区为例，七段矢量依次为V₀、V₁、V₂、V₇、V₂、V₁和V₀。一个开关周期内的三相输出电压都是中间对称的单脉冲。因此可以用一个幅值为-1～1的对称三角波作为载波，与三个参考值m_a、m_b、m_c比较生成，如图2-16所示。根据冲量等效原则，三相参考值可以通过式（2-9）计算得到。直流电压为V_dc的变换器的三相输出电压表示为式（2-10）。

图2-16 载波比较PWM与空间矢量PWM的对应（以第一扇区为例）

而将式（2-9）中的三相调制函数相加，得到共模调制函数如式（2-11）所示。之前已经解释过，由于输出线电压中相电压相减，可以把三相的共模调制函数减掉。得到的a-b和b-c的线电压如式（2-12）所示，可以看出线电压与零矢量无关。因此这个共模调制函数是一个不影响输出有效电压的量，也是不同PWM方式的一个主要区别。

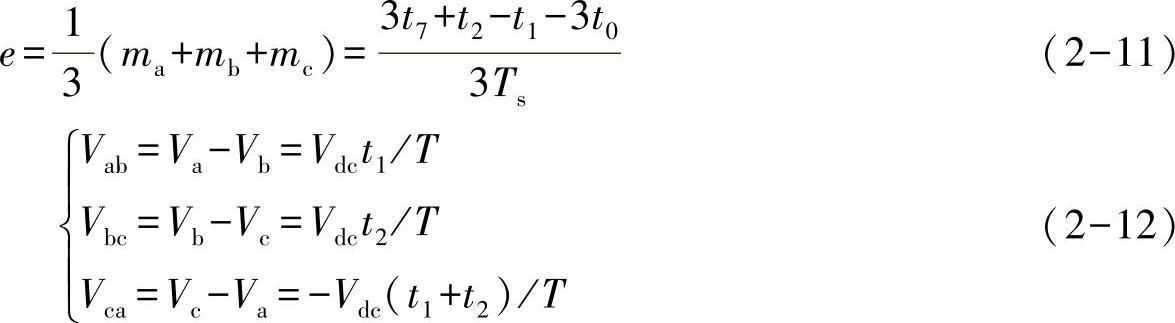
在式（2-9）中，矢量V₁和V₂的作用时间t₁和t₂都是通过式（2-4）得到的。即当参考电压矢量确定时，这两段时间也是确定的。但是由于000和111这两个零矢量的作用效果是相同的，开关周期T_s中剩余的时间t_zero如何分配给t₀和t₇则是可以控制的。定义一个参数k，满足0≤k≤1，用于调节000和111作用时间在总的零矢量时间中的比例，如式（2-13）所示。k越大表明000矢量作用时间占的比例越高，反之111矢量作用时间占的比例越高。

以上描述都是针对第一扇区的分析结果。对六个不同扇区都可以进行类似的分析，得到如表2-3所示的结果。

表2-3 六个扇区内的空间矢量时间分配和共模调制分量[5]

表2-3中，每个扇区内的非零矢量作用时间都可以归为式（2-4）中计算得到的相邻两个矢量的作用时间表达式。统一表达式得到的共模调制函数如式（2-14）所示。由于k可以任意配置，所以所有的载波比较PWM通过求其共模调制函数e，再求解式（2-14）就可以得到其对应的空间矢量PWM的零矢量分配系数k，而所有的空间矢量PWM方式都可以通过注入合适的e得到其对应的载波比较PWM方法。

e=k（1-m_max）+（1-k）（-1-m_min） （2-14）

首先分析SPWM和HIPWM这两种载波比较PWM对应的空间矢量PWM方式。

对于最普通的三相正弦PWM，由于三相参考电压是互差120°的标准正弦波，如式（2-7）所示，其共模调制分量e=0。求解式（2-14）得到k的表达式如式（2-15）所示。这样，通过空间矢量PWM得到t₁和t₂之后，就可以按照式（2-15）和式（2-13）得到000和111矢量作用的时间。

(www.xing528.com)

对于式（2-8）所示的三次谐波注入型PWM，共模调制函数为e=μmcos（3ω₀t），代入式（2-14），得到k的表达式如式（2-16）所示。这样HIPWM也可以通过式（2-16）和式（2-13）得到000和111矢量作用时间分配比例，然后得到对应的SVPWM。

图2-17展示了调制比为0.9时，SPWM和HIPWM等效为SVPWM中000和111矢量作用时间分配比例在一个基波周期的变化。

图2-17 等效空间矢量PWM中000和111矢量作用时间的分配

a）SPWM b）HIPWM

通过载波比较PWM能对应得到空间矢量PWM的等效结果之外，还可以通过式（2-14）得到空间矢量PWM对应的载波比较PWM。即通过式（2-14），得到空间矢量PWM对应载波比较PWM的共模调制函数e，从而得到对应的三相参考值m_a、m_b和m_c。这样得到的载波比较PWM与对应的空间矢量PWM在输出效果上就是一致的了。

对于七段式SVPWM，直接设置了k=0.5，即000和111矢量的作用时间一样，t₀=t₇。此时共模调制函数为e=0.5（1-m_max）+0.5（-1-m_min）。

对于五段式DPWM，000和111矢量中只有一个被应用：DPWMMin对应于k=0；DP-WMMax对应于k=1。而最小开关损耗的DPWM1则根据电流方向在k=1和k=0两种状态之间切换。三种情况对应的共模调制函数如式（2-17）所示。

这样，就可以得到SVPWM、DPWMMin、DPWMMax和DPWM1这四种空间矢量PWM的调制函数及共模调制函数，如图2-18所示。其中，DPWM1是在单位功率因数情况下得到的，即调制函数与电流是同相位的。图2-18中，选取了正弦波的调制比为0.9这一典型值。

图2-18 典型的调制函数与共模调制分量

a）SVPWM b）DPWMMin c）DPWMMax d）DPWM1

由于SVPWM和DPWM都可以通过SPWM的调制函数叠加共模调制分量e来实现，所以用载波比较PWM的方式实现空间矢量合成是可行的。图2-19所示为通过载波比较实现SVPWM和DPWM的框图。在SPWM的基础上，通过三相占空比计算共模调制分量e，叠加在SPWM对应的占空比之上，就得到了SVPWM或者DPWM的参考波。在理论上这与三角载波比较PWM和空间矢量合成SVPWM或者DPWM是一致的。这样的方法与空间矢量合成相比，实现简单，适合在数字控制中应用。

图2-19 通过载波比较方法实现SVPWM和DPWM