单桥臂载波比较PWM与正弦PWM的比较

空间矢量PWM通过在三相系统中虚构一个二维的平面，通过矢量合成的方法实现脉冲电压对连续参考电压的逼近。另一种PWM的逼近方法则直接通过伏秒平衡或者冲量等效原理来实现，即载波比较PWM实现方法，在第1章中也简单地描述过这种方法。

图2-8所示是单桥臂载波比较PWM的基本结构。单桥臂中正负母线电压相对直流母线中点分别为V_dc/2与-V_dc/2，输出端V_x电压需要逼近参考电压。参考电压与高频的三角载波比较后，根据参考电压高于或者低于三角载波的值决定桥臂上下开关管的门极驱动信号，从而决定V_x如何切换于正负母线电压之间。

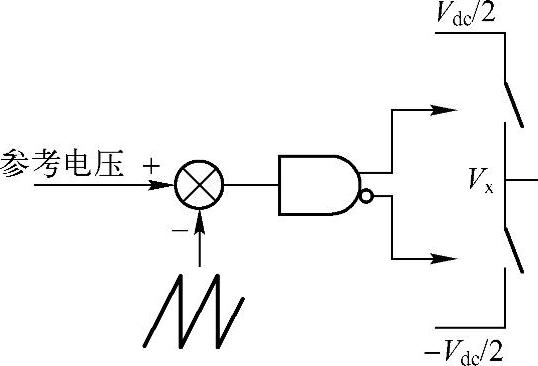
图2-8 单桥臂的载波比较PWM的基本结构

图2-8中的参考电压是任意的连续电压，既可以是正弦电压也可以是非正弦电压，但是频率必须低于载波的频率才能通过载波比较PWM实现逼近。而载波也可以是不同的三角波序列，三角波状态的不同不会影响输出电压的平均值，但是会影响输出脉冲电压的位置。图2-9所示为四种情况下的三角载波在一个开关周期内的比较输出。三角载波的两个端点为V_dc/2和-V_dc/2，与参考电压V_ref比较后输出电压V_x是切换于V_dc/2和-V_dc/2的方波脉冲。图2-9a、b所示是两种极端情况，即三角载波为直角三角形，而直角边分别与此开关周期的左侧和右侧对齐，此时的三角波为锯齿波形态，因此发出的方波脉冲分别右对齐和左对齐于开关周期。图2-9c所示为一种普适的情况，即三角波的顶点在开关周期内任意分布，而三角波两侧的斜边也可以有任意的斜率。在这种情况下发出的脉冲电压的上升沿和下降沿也可以在开关周期内任意分布，但是保证它们之间的距离固定。图2-9d则是中间对齐的三角载波的情形，即三角载波顶点在开关周期正中间，三角载波为等腰三角形。此时发出的脉冲电压则为中间对称的脉冲电压。因为根据相似三角形的关系，开关周期T_s内的脉冲电压低电平时间T₀满足T₀/T_s=（V_dc/2-V_ref）/V_dc，所以参考电压就决定了输出脉冲电压在开关周期内的占空比，而三角波的形态决定的是脉冲在开关周期内的位置。在实际应用中，图2-9d所示的对称三角载波应用最为广泛，也是载波PWM与七段式或者五段式SVPWM对应的方式。但是载波变化实现脉冲位置不同可以作为一个自由度改变系统的性能，在后续章节中会详细介绍。

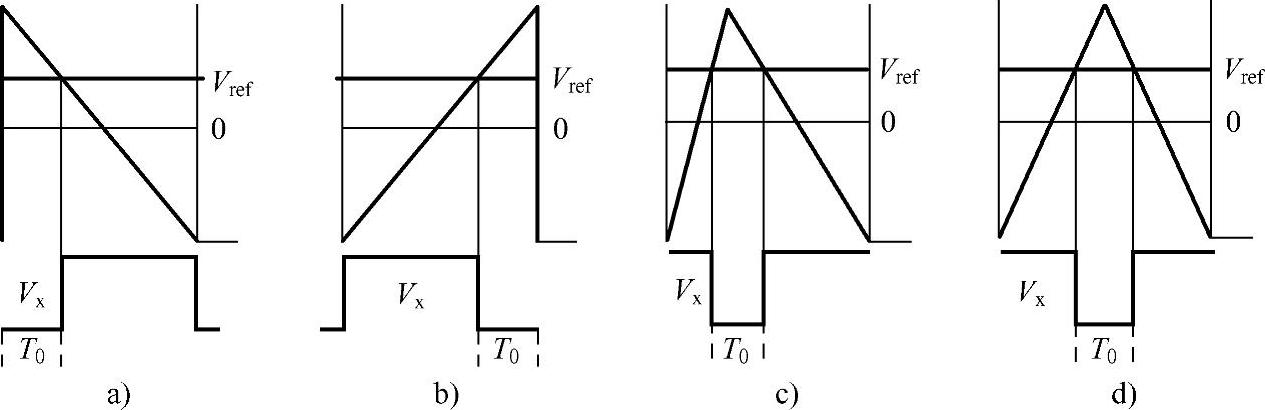
图2-9 三角载波及其在一个开关周期的比较输出

a）左侧对齐锯齿波 b）右侧对齐锯齿波 c）任意三角波 d）中间对齐三角波

讨论了载波的形态之后，还需要讨论参考波的形态。采用连续参考波与三角载波比较时主要有两种方式，即自然采样和规则采样的方法，如图2-10所示。图2-10a所示是自然采样的载波比较PWM，即连续的参考电压V_ref直接与三角载波序列进行比较，V_ref与载波的交点决定了输出脉冲电压的上升沿和下降沿。这种方式能够比较准确地逼近参考电压，因为连续的参考电压是直接与载波进行比较输出的，但是由于参考电压的连续变化，与载波上升和下降的交界点也会有较小的变化，因此导致脉冲有一定程度的不对称。自然采样多用于模拟电路发生PWM的电路中，因为在模拟系统中参考电压是连续的，可以直接用于比较，但是在目前广泛应用的数字系统中，采样周期内参考电压是固定不变的，所以就衍生出了图2-10b的规则采样PWM方式。在规则采样的PWM模式下，每个开关周期的参考电压是固定值，图2-10b中，参考电压V_ref通过数字采样的方式在开关周期内变为恒定值与载波比较发生PWM，由于参考电压的固定值，其与对称三角载波的上升和下降交界点也是对称的，发出的脉冲电压在开关周期内也是对称的。在开关频率远高于参考电压频率的场合，连续参考电压与被采样后的阶梯参考电压非常接近，因此规则采样得到的脉冲电压序列也可以逼近参考电压。这种方法广泛应用于以数字信号处理器（DSP）为主的数字系统中。采样的位置在开关周期中一般位于采样周期的中间，也可以为其他位置。同时，一个开关周期内如果有多次采样，波形则更接近连续参考电压。

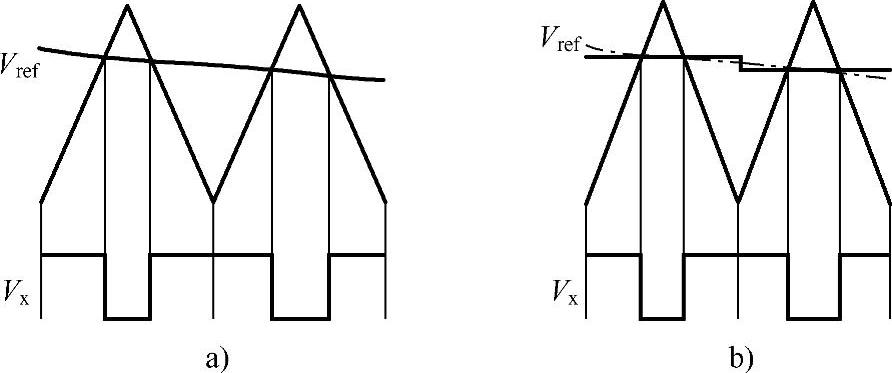
图2-10 载波比较的两种形态

a）自然采样 b）规则采样

对称三角载波比较和规则采样是数字控制系统中最常用的载波比较PWM方式，本书的载波比较PWM的介绍一般都基于这两种模式。

在三相系统的载波比较PWM中，根据应用的不同，参考电压也可以不同。最常见的应用就是正弦PWM（SPWM）及其拓展。正弦PWM指的是三相参考电压按照对称的正弦函数发生的载波比较PWM。如果归一化到-1～1之间，可以定义三相参考值为

式中，m是归一化到0～1的三角函数幅值，代表调制比，即输出相电压峰值与一半直流母线电压之比。三相对称正弦参考值与幅值为-1～1的对称三角载波比较，发出PWM的结果如图2-11所示，当对应的正弦参考值大于三角波时，对应桥臂输出电压为1，即正直流母线电压值V_dc/2；而对应的正弦参考值小于三角波时，对应桥臂输出电压为-1，即负直流母线电压值-V_dc/2。这样发出的三相相电压脉冲序列在每个开关周期内的平均值都逼近对应正弦参考电压，使输出电压的基波分量也逼近三相正弦电压。(www.xing528.com)

图2-11采用的是自然采样比较的方法，因此三相参考电压m_a、m_b和m_c都是连续量，与三角波比较的位置在开关周期内也是不对称的。数字控制中采用采样保持器使三相参考电压离散化，实现了规则采样的结果如图2-12所示。此时三相参考电压是离散的，在每个开关周期内不变，因此输出相电压在开关周期内也是对称的。

图2-12 三相SPWM的参考波、载波及三相输出相电压（规则采样）

输出相电压互相相减就得到加载在三相负载上的线电压。图2-13所示为三相SPWM下输出的线电压波形，线电压脉冲序列呈现三电平特征，幅值为2，即表示瞬时的线电压为正直流母线电压V_dc或者负直流母线电压-V_dc。

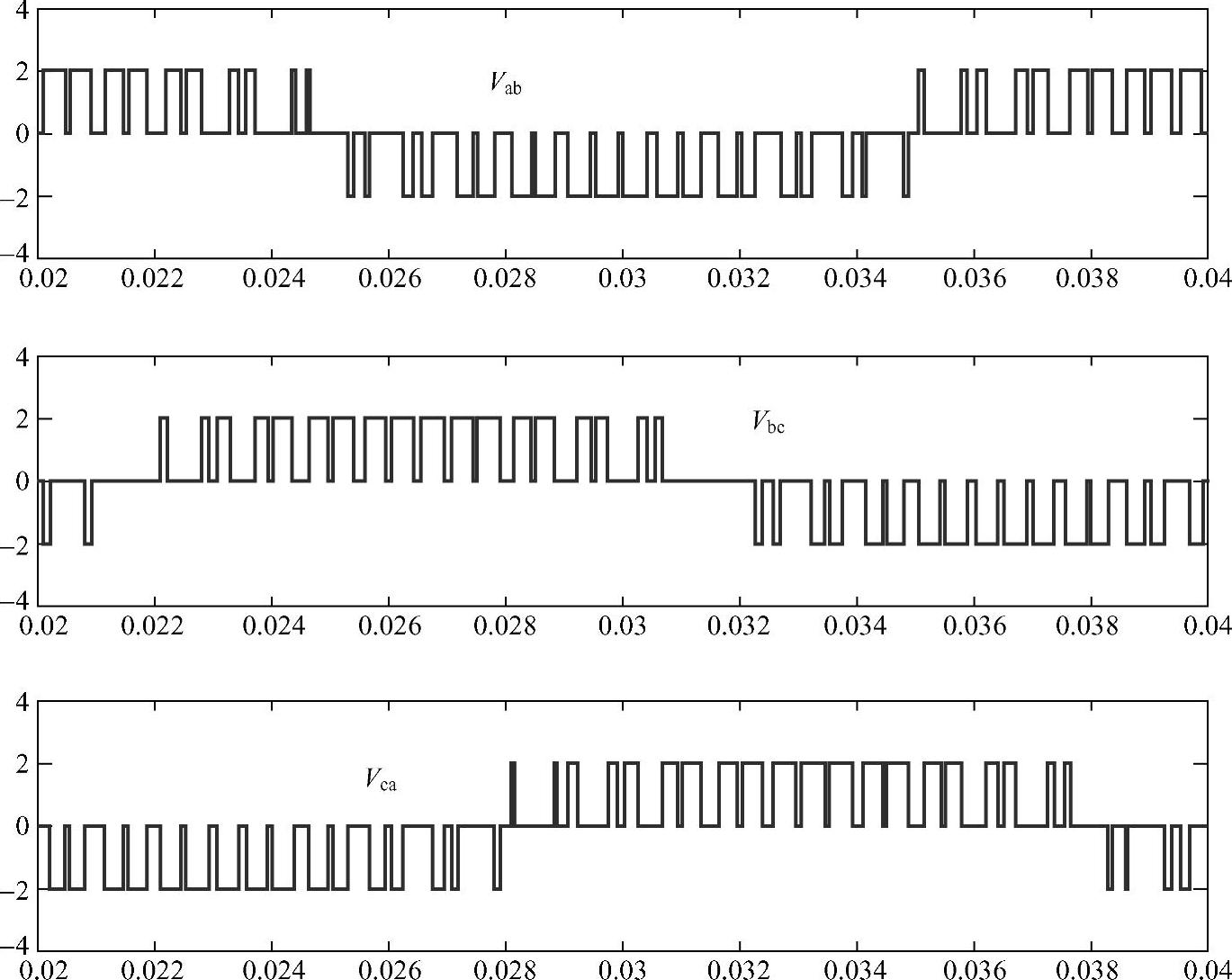
图2-13 三相SPWM下输出的线电压波形

但是SPWM存在一个问题，即式（2-7）中的调制比m不能超过1，否则参考波幅值大于三角波幅值，就会出现过调制的现象。图2-14所示是m=1.1时的过调制现象，此时有部分区域参考波恒大于或者恒小于载波，使载波比较失效，变换器不进行开关动作，输出电压也不能逼近参考电压。

图2-14 三相SPWM在过调制下的波形

由于调制比的限制，SPWM最大输出相电压只能等于直流母线电压的一半，这和式（2-6）中SVPWM中输出相电压可以达到直流母线一半电压的1.1547倍相比，调制比降低为SVPWM的0.866倍。为了提高调制比，在SPWM基础上又发展出了三次谐波注入的载波比较PWM。

因为最后加载在负载上的是线电压，所以如果在相电压的三个调制波上叠加一个相同的分量，求线电压时两两相电压相减，最后得到的效果和叠加共同分量之前是一致的。因此可以通过注入合适的叠加分量将正弦电压峰值降低，从而能够实现更高的输出电压。最典型的就是注入三次谐波电压。式（2-8）展示了三次谐波注入的载波比较PWM，又称为HIPWM。在SPWM的三相参考电压基础上三相都叠加了同一个三次谐波μcos（3ω₀t）。通过求解函数最小峰值，得到当μ=-1/6时，式（2-8）括号内部分的峰值最小，为0.866。此时的m即使增加到1.1547也能满足参考波最大值不超过1，从而能实现和SVPWM一样的调制比。

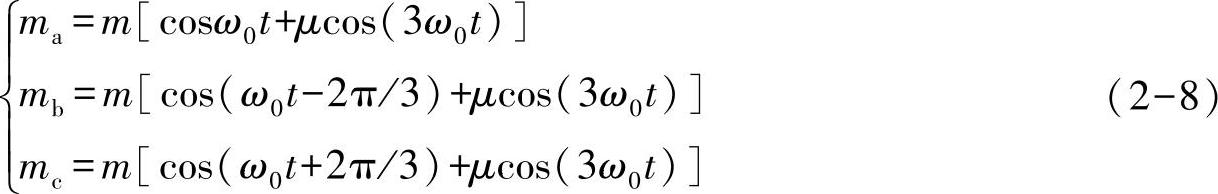
图2-15所示是三相HIPWM在m=1.1时的参考波、载波和三相输出相电压。和图2-14比较，采用HIPWM，即使m=1.1，由于注入的三次谐波有效地降低了原始正弦参考波的峰值，仍然保持时域内参考波在-1～1之间，没有出现过调制和开关不连续的情况。这样的输出线电压与注入三次谐波之前的正弦线电压是一致的。这个结果证明HIPWM能够有效地提高SPWM的载波比和输出电压利用率。

图2-15 三相HIPWM的参考波、载波和三相输出相电压