数据运算器设计与应用：以加法器为例

常用的数据运算器包括加法器、乘法器、比较器、计数器和寄存器等，其中加法器是最基本的数据运算器，其他各种数据运算器可以以加法器为基础来进行设计。下面以比较基础的加法器为例来分析数据运算器的设计过程。

1.一位加法器

加法器是构成很多系统的重要部件。一位加法器是加法器的基础，其他多位加法器可以在此基础上进行复杂的设计。一位半加器和全加器的示意图如图4-15所示。

对应的真值表见表4-1和表4-2。

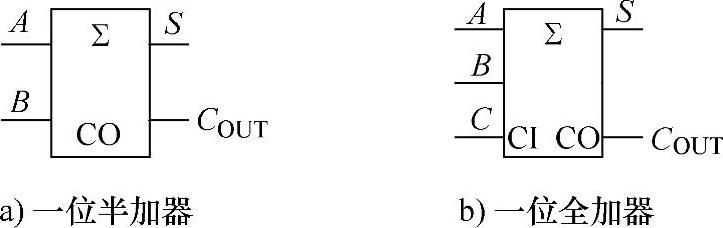
图4-15 一位半加器和全加器的示意图

表4-1 一位半加器的真值表

表4-2 一位全加器的真值表

其中A、B是加法器的输入，C是上一级进位输入，S是和输出，C_OUT是进位输出。

因为A和B相加后结果可能是0、1、10（二进制），因此表示结果需要两位二进制数，分别称为S（Sum，本位和）和C_OUT（Carry-Out，向高位的进位）。

根据上面的真值表，我们可以得出一位半加器的逻辑表达式：

S=A⊕B

C_OUT=AB （4-22）

根据此表达式可以直接利用前面学过的知识点设计出对应的电路图。由表达式可以看出，一个一位半加器由一个异或门和一个与门实现，此处不再详细讲解。一位半加器的门级电路如图4-16所示。

同样道理，也可以根据一位全加器的真值表化简出一位全加器的表达式，进而根据表达式设计出对应的电路图。

一位全加器的逻辑表达式：

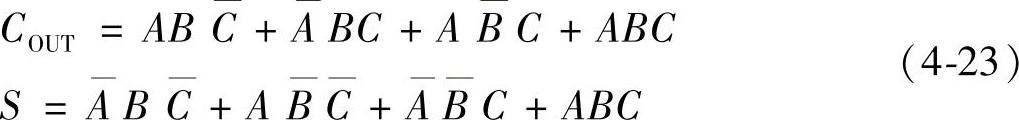
此表达式可以进一步化简得到对应的简化表达式。(https://www.xing528.com)

C_OUT=AB+（A⊕B）C

S=A⊕B⊕C （4-24）

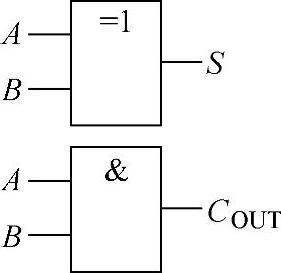
图4-16 一位半加器的门级电路

不管如何化简，表达式的最终形式都比较复杂，需要很多基本逻辑门来实现。

其实我们完全可以利用刚才设计好的一位半加器来实现一位全加器。分析一位全加器的加法过程可以知道，一位全加器的加法过程相当于三个一位半加器的加法过程。一位全加器的运算过程如图4-17所示。

根据图4-17所示一位全加器的运算过程，可以很容易地设计出对应的逻辑图，一位半加器组成的一位全加器的示意图如图4-18所示。

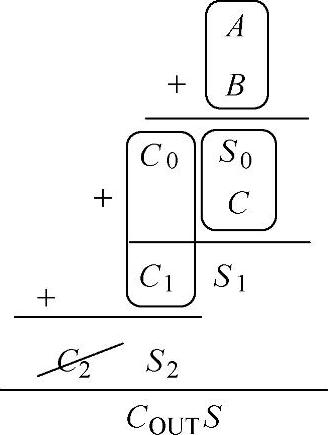
图4-17 一位全加器的运算过程

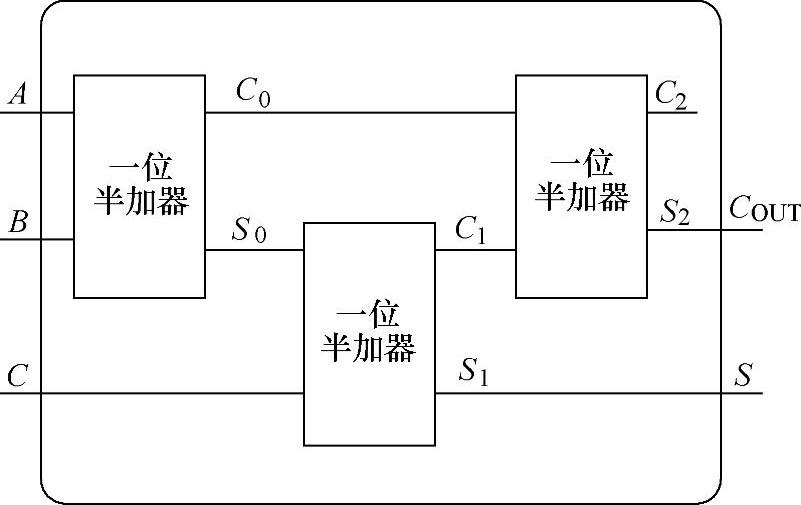
图4-18 一位半加器组成的一位全加器的示意图

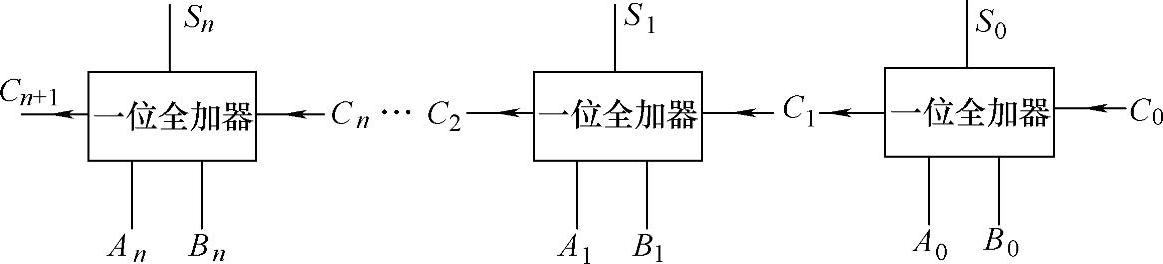
图4-19 多位加法器的示意图

在图4-18中，一位全加器由三个一位半加器组成，大家注意，第三个一位半加器的进位输出端没有连接，也就是第三个一位半加器的电路没有全部用到，因此在此电路中，第三个一位半加器可以用一个异或门代替（因为一位半加器的和S为输入端的异或）。

在实际的设计中，一位全加器有很多种设计方法，例如可以采用传输门和异或门来设计一位全加器。此处不再详述，读者可以去查阅相关的资料文献。

2.n位加法器

在实际的电子系统中，其运算单元一般是进行多位二进制数的运算。例如，常见的32位CPU中的运算单元可以进行32位二进制数的运算，此时就要用到多位加法器。

比较常规的多位加法器设计过程如下：一个n位加法器可以由n个一位全加器串联构成，多位加法器的示意图如图4-19所示。在设计这种电路的过程中，一定要注意最终的结果书写顺序。此图中最后的加法结果为C_n+1S_n…S₁S₀。

但这种设计方法存在一个问题，就是随着串联一位全加器的增多，信号在传输过程中的延迟越来越大，反而会影响电路的性能。