设两个被比较量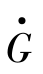 和
和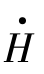 ,
, =G∠αG,
=G∠αG, =H∠αH,比较二者的相位,当它们的相位差满足某一关系时,比相器有输出,或称“动作”。根据动作范围不同,通常可分为正弦型和余弦型两种。
=H∠αH,比较二者的相位,当它们的相位差满足某一关系时,比相器有输出,或称“动作”。根据动作范围不同,通常可分为正弦型和余弦型两种。
两种形式的动作条件为:
余弦型:
正弦型:
其中, 超前于
超前于 为正,其动作特性如图3.9所示。上两式可等效为:
为正,其动作特性如图3.9所示。上两式可等效为:
cos(αG-αH)=cosαGcosαH+sinαGsinαH≥0
sin(αG-αH)=sinαGcosαH-sinαGcosαH≥0
两边同乘以G和H得:
G cosαGH cosαH+G sinαGH sinαH≥0
G sinαGH cosαH-G sinαGH cosαH≥0
图3.9 正弦型和余弦型比相器的动作特性
①傅氏算法。
上式表明,只要用傅氏算法算出两个被比较量 和
和 的正弦和余弦分量系数,就可以实现比相,式(3.57)与式(3.55)、式(3.56)等效。
的正弦和余弦分量系数,就可以实现比相,式(3.57)与式(3.55)、式(3.56)等效。
②两点乘积算法。
其中,g1、g2、h1、h2分别为两个相隔1/4周期采样时刻t1、t2时的 和
和 的采样数据,该式与式(3.55)、式(3.56)等效。
的采样数据,该式与式(3.55)、式(3.56)等效。
③动作范围不为180°,可用两个范围为180°的元件组合而成。以余弦型为例,若将图3.9中的特性转动θ0角,则式(3.55)可写成:
图3.10 转动±θ0时余弦型特性(https://www.xing528.com)
将上式变成如式(3.55)的标准形式:
其特性如图3.10所示,其中,+θ0表示特性逆时针方向转动,-θ0表示特性顺时针方向转动。
对于+θ0,式(3.59)等效于cos(aG-aH+θ0)≥0,展开整理后得:
(cos aGcos aH+sin aGsin aH)cosθ0-(sin aGcos aH-sin aHcos aG)sinθ0≥0
傅氏法:
(GSHS+GCHC)cosθ0-(GCHS-GSHC)sinθ0≥0
两点法:
(g2h2+g1h1)cosθ0-(g1h2-g2h1)sinθ0≥0
对于-θ0,式(3.59)等效于cos(aG-aH-θ0)≥0,展开整理后得:
(cos aGcos aH+sin aGsin aH)cosθ0+(sin aGcos aH-sin aHcos aG)sinθ0≥0
傅氏法:
(GSHS+GCHC)cosθ0+(GCHS-GSHC)sinθ0≥0
两点法:
(g2h2+g1h1)cosθ0+(g1h2-g2h1)sinθ0≥0
+θ0和θ0元件的动作范围都是180°,将二者组合起来,可以得到大于或小于180°的动作范围。若要二者都动作时才动作,即取二者的“与”,动作角度范围-90°+θ0<θ<90°-θ0,动作范围小于180°;若只要满足其中一个动作条件即动作,则动作角度为-90°-θ0<θ<90°+θ0,动作范围大于180°。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




