直接移相原理的序分量滤波器优化方案：

这种序分量滤过器是基于对称分量基本公式（以电压为例）：

对于序列3u1、3u2、3u0相应的有公式：

只要知道了a、b、c三相的采样序列，经过移相±120°后，按上式运算即可得到正序、负序和零序分量的序列，相当于各序分量的采样值。设每周采样12点，即N=12，ωTs=30°，根据移相时的数据窗不同，可有下列几种算法。这里先说明相量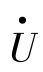的相位变化情况。随时间变化，相量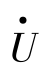的相位由0°～360°呈周期性变化，这相当于相量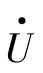在复平面上周而复始地旋转。设t=nTs时，的相位为0°，此时，采得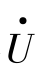的瞬时值为u（n）。当t=（n-K）Ts时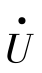，的相位相对于t=nTs时滞后KωTs角度，对应此时的采样值为u（n-K）。显然，若取ωTs=30°，当K分别为8和4时，相量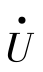已旋转了240°和120°，此时，所对应的采样值分别为u（n-8）和u（n-4），如图3.4所示。

图3.4　相量相位变化

（1）数据窗K=8时

由图3.4可以看出：

au(n)=u(n-8)

a2u(n)=u(n-4)

于是有：

3u1(n)=ua(n)+ub(n-8)+uc(n-4)

3u2(n)=ua(n)+ub(n-4)+uc(n-8)

3u0(n)=ua(n)+ub(n)+uc(n)

上式表明，只要知道了a、b、c三相的电压在n、n-4、n-8三点的采样数据，就可以由上式计算出各序在n时刻的值。本算法的数据窗K=8，时窗KTs=13.3 ms。

（2）数据窗K=4时

由图3.5可见，au（n）可以表示为-u（n-2），a2u（n）=u（n-4），于是有：

3u1(n)=ua(n)+aub(n)+a2uc(n)

=ua(n)-ub(n-2)+uc(n-4)

3u2(n)=ua(n)+a2ub(n)+auc(n)

=ua(n)+ub(n-4)-uc(n-2)(www.xing528.com)

在此，以负序为例来分析其正确性。图3.5（a）是正序输入时的相量关系，因ua1（n）、ub1（-4）、-uc1（n-2）三者对称，故3u2（n）输出为0；图3.5（b）是负序输入时的相量关系，因ua2（n）、ub2（n-4）、-uc2（n-2）三者同相，故3u2（n）输出很大，其值为3ua2（n）。

图3.5　K=4时的负序元件相量分析图

同理，可以分析正序元件在正序输入时有输出，而在负序输入时输出为0。

（3）数据窗K=2时

由图3.6可见：

a2u(n)=u(n)e-j60°-u(n)=u(n-2)-u(n)

au(n)=-u(n-2)

因此，有

3u1(n)=ua(n)+aub(n)+a2uc(n)

=ua(n)-ub(n-2)+uc(n-2)-uc(n)

3u2(n)=ua(n)+a2ub(n)+auc(n)

=ua(n)+ub(n-2)-ub(n)-uc(n-2)

因a2=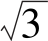e-j30°-2；a=1-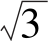e-j30°

（4）数据窗K=1时

故

图3.6　K=2时的相量关系

图3.7　K=1时的相量关系