最简单的单位系数数字滤波器实现方法

（1）差分（相减）滤波器

差分（相减）滤波器是一种简单的数字滤波器，其滤波差分方程为：

式中　K——差分步长，根据不同的滤波要求给定的整常数，K≥1。

采用Z变换法可由差分方程得到该滤波系统转移函数为H（z）=1-z-K，令z=ejωTS得到其频域响应特性为：

H(ω)=1-e-jωTSK=1-cos(ωTSK)+j sin(ωTSK)

图2.5　差分滤波器幅频特性

若取每基频周期内采样点数为N、基频频率为f1，则有将此关系代入上式，可得到差分滤波器的幅频特性为：

请注意，频率响应特性中f的变化范围应满足采样定理要求，即式（2.16）中若设，其幅频特性曲线如图2.5所示。当取f=m fm（m=1，2.3，…）时，，表明经差分滤波后输入信号中的直流分量以及频率为fm和fm的整次谐波分量将被完全滤出。当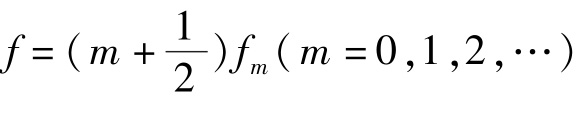时，有一系列等幅极大值=2，这表明经差分滤波后输入信号中所有对应此频率的谐波将会得到等幅的最大输出。通过合理地选择（或控制）参数N与K可以控制滤波器的滤波特性。

在数字保护装置中，差分滤波器主要有下述用途。(www.xing528.com)

①消除直流和某些谐波分量的影响。但需要指出的是，差分滤波器对故障信号中的某些高频分量有放大作用，因此，一般不能单独使用，需要与其他的数字滤波器和算法配合使用，以便得到良好的综合滤波效果。

②抑制故障信号中的衰减直流分量的影响。利用差分滤波器可以完全滤除恒定直流分量，也可对衰减直流分量起到良好的抑制作用。为获得最好的抑制衰减直流分量的效果，需要合理地选择数据窗。通常数据窗越短，取K=1抑制衰减直流分量的效果越好，但需要综合考虑对其他有用信号的不利影响。

（2）积分滤波器

积分滤波器也是一种常用的简单数字滤波器，其滤波方程为：

式中　K——积分区间，常数，可按不同的滤波要求选择，K≥1。

积分滤波器的幅频特性为：

若设，其幅频特性曲线如图2.6所示。当f=mfm（m=1，2，…）时，=0，对应此频率的谐波分量将被完全滤除；时，有一系列极值点，而当f=0时，得到其最大值，且随f的增大，在其他的极值点上逐步减小[并均小于这表明积分滤波器不能滤除输入信号中的直流分量和低频分量，但对高频分量有一定的抑制作用，并且频率越高抑制作用越强。进一步考虑取，即取积分区间或数据窗约为半个基频周期时，fm=2f1，表明此时积分滤波器可滤除所有的偶次谐波分量。

上述差分和积分滤波器的结构非常简单，并具有单位系数的特点，计算量很小，但各自独立使用时，滤波特性难以满足数字式保护有效信号提取的要求。