失磁发电机机端阻抗变化特性测量方法探究

测量阻抗定义为从发电机端向系统方向所看到的阻抗。

（1）等有功阻抗图（δ＜90°）

如上所述，发电机由失磁开始至临界失步是一个等有功过程，即P为恒定，则机端测量阻抗为：

式中，θ=

因为P不变，再假设XS、US均为恒定，只有角度θ为变数，故式（6.30）在阻抗复平面上的轨迹为一圆，其圆心坐标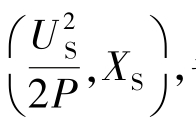为半径为如图6.19所示。此圆称为等效有功阻抗圆。分析式（6.30），可以得出以下结论：

①一定的等有功阻抗圆与某一确定的P相对应，其圆半径与P成反比（圆周上各点P为恒量而θ为变量），即发电机失磁前带的有功负荷P越大，相应的圆越小。

②发电机正常运行时，向系统送出有功功率和无功功率，θ角为正，测量阻抗在第一象限。发电机失磁后无功功率由正变负，θ角逐渐由正值向负值变化，测量阻抗也逐渐向第四象限过渡。失磁前，发电机送出的有功功率越大（圆越小），测量阻抗进入第四象限的时间就越短。

图6.19　等有功阻抗圆

③等有功阻抗圆的圆心坐标与联系电抗XS有关，在同一功率下，不同的XS，对应着不同的轨迹圆。如XS=0，则圆心坐标在R轴上，测量阻抗很易进入第四象限，XS较大（即机组离系统较远），圆心坐标上移，则其测量阻抗不易进入第四象限。可以看到，失磁发电机的机端测量阻抗的轨迹最终都是向第四象限移动。

（2）等无功阻抗圆（δ=90°）

这时的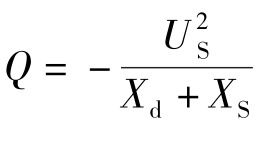，即发电机从系统吸收无功功率，发电机机端测量阻抗为：

将代入上式得：

式中，US、XS和Q为常数时，式（6.32）是一个圆的方程。

圆心坐标为，半径为，如图6.20所示。此圆称为等无功阻抗圆，也称临界失步阻抗圆或静稳极限阻抗圆，圆外为稳定工作区，圆内为失步区，圆上为临界失步。该圆的大小与Xd、XS有关系。XS越大，圆的直径越大，且在第一、二象限部分增加，但无论Xd、XS为何值，该圆都与点（0，-jXd）相交。

图6.20　临界失步（或静稳极限阻抗圆）

图6.21　发电机异步运行等值电路

（3）稳态异步运行阻抗圆

失步后的阻抗轨迹，最终将稳定在第四象限，这是因为进入稳态异步运行后，同步发电机成为异步发电机，其等效电路与异步电动机类似。如图6.21所示，圆中的X1为定子绕组漏抗，X′2为转子绕组的归算电抗，Xad为定子、转子绕组间的互感电抗（即电枢反应电抗），R′2为转子绕组的计算电阻，S为转差率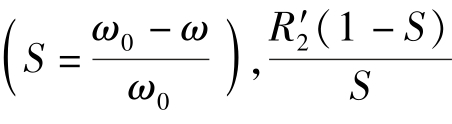则表示发电机功率大小的等效电阻。由图6.21可得，此时发电机的测量阻抗为：

上式表明，此时发电机的测量阻抗与转差率S有关。(www.xing528.com)

考虑两种极端情况：

①发电机空载运行失磁时，此时测量阻抗最大，即

Z=-(jX1+jXad)=-jXd

②发电机在其他运行方式失磁时，取极限情况，即此时测量阻抗最小，即

图6.22　异步运行阻抗圆

以-jXd和-jX′d为两个端点，并取Xd-X′d为直径，也可以构成一个圆，如图6.22所示。它反映稳态异步运行时Z=f（S）的特性，简称异步运行阻抗圆，也称抛球式阻抗特性圆。发电机在异步运行阶段，机端测量阻抗进入临界失步阻抗圆内，并最终落在-jX′d～-jXd的范围内。

（4）临界电压阻抗圆

为了保证在失磁后系统稳定及厂用电安全，要求机端电压Ug不得低于某一定值，这一电压定值称临界电压值。在临界电压为一定的条件下，机端测量阻抗的轨迹，同样可用阻抗圆描述。

在如图6.23所示的简化网络图中，当发电机失磁后，若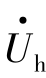下降到小于等于系统电压为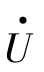的K倍，即Uh≤KU（K＜1），则会危及系统及厂用电的安全。

从网络图中可得：

上两式两端同除以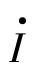，得：

两电压大小的比值等于两阻抗比值的绝对值，即

将Z=R+jX代入上式得：

图6.23　发电机与系统的简化网络

Xst—主变电抗；Xs1—主变以外的系统电抗；Uh—主变高压侧电压

图6.24　临界电压阻抗圆

式中，Xs1、Xst、K均为已知系数。机端测量阻抗的轨迹为一圆，称临界电压阻抗圆，如图6.24所示，其圆心坐标为半径为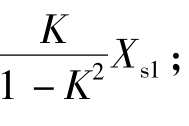对于确定的R值，均有一个确定的临界电压阻抗圆与之对应。当机端测量阻抗进入该圆时，说明主变高压侧电压低于允许值，应将失磁发电机切除。汽轮发电机通常可用此圆来确定跳闸动作区。