电力系统振荡对距离保护的影响及振荡闭锁回路的优化方案

当电力系统中发生同步振荡或异步运行时，各点的电压、电流和功率的幅值和相位都将发生周期性变化。电压与电流之比所代表的阻抗继电器的测量阻抗也将周期性变化。当测量阻抗进入动作区域时，保护将发生误动作。因此，对于距离保护必须考虑电力系统同步振荡或异步运行（以下简称系统振荡）对其工作的影响。

（1）电力系统振荡时电压电流的分布

电力系统中由于输电线路输送功率过大，超过静稳定极限，由于无功功率不足而引起系统电压降低，或由于短路故障切除缓慢，或由于非同期自动重合闸不成功，这些因素都可能引起系统振荡。

下面以两侧电源辐射型网络（图2.30）为例，说明系统振荡时各种电气量的变化。如在系统全相运行（三相都处于运行状态）时发生系统振荡，此时，三相总是对称的，可以按照单相系统来研究。

图2.30　两侧电源系统中的振荡

图2.30（a）为一两机系统接线图，图上给出系统和线路的参数以及电压电流的假定正方向。如以电势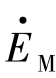为参考，使其相位角为零，则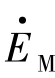=EM。在系统振荡时，可认为N侧系统等值电势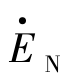围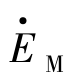旋转或摆动，因而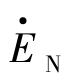落后于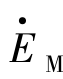之角度δ在0°～360°变化。

由M侧流向N侧的电流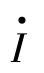为：此电流滞后于电势差的角度为系统总阻抗角φz：

在振荡时，系统中性点电位仍保持为零，故线路两侧母线的电压和为：

按照上述关系式可画出相量图如图2.30（b）所示。以为实轴，落后于的角度为δ，连接和相量端点得到电势差加ZN上的电压降得到N点电压从减去ZM上的压降后得到M点电压当系统阻抗角等于线路阻抗角，即等于总阻抗的阻抗角，故和的端点必然落在直线（）上。相量（）代表输电线上的电压降。如果输电线是均匀的，则输电线上各点电压相量的端点沿着直线（）移动。从原点与此直线上任一点连线所作的相量即代表输电线上该点的电压。从原点作直线（）的垂线所得的相量最短，垂足Z所代表的输电线上那一点在振荡角度δ下的电压最低，该点称为系统在振荡角度为δ时的电气中心或称振荡中心。当系统阻抗角和线路阻抗角相等且两侧电势幅值相等时，电气中心不随δ的改变而移动，始终位于系统总阻抗（ZM+ZL+ZN）的中心，电气中心名称即由此而来。当δ=180°时，振荡中心的电压将降至零。从电压电流的数值看，这和在此点发生三相短路现象类似。但是，系统振荡属于不正常运行状态而非故障，继电保护装置不应动作切除振荡中心所在的线路。因此，继电保护装置必须具备区别三相短路和系统振荡的能力，才能保证在系统振荡状态下的正确地工作。图2.30（c）所示为系统阻抗角与线路阻抗角不相等的情况，在此情况下电压相量和的端点不会落在直线（）上。如果线路阻抗是均匀的，则线路上任一点的电压相量的端点将落在代表线路电压降落的直线（）上。从原点作直线（）的垂线即可找到振荡中心的位置及振荡中心的电压。不难看出，在此情况下振荡中心的位置随着δ的变化而变化。

对于在系统振荡状态下的电流，仍以图2.30（a）的两机系统为例。式（2.49）为振荡电流随振荡角度δ而变化的关系式。

令

h=EN/EM表示两侧系统电势幅值之比，则

或

设以为参考相量，，则

由此可知，振荡电流的幅值与相位都与振荡角度δ有关。只有当δ恒定不变时，IM和θ为常数，振荡电流才是纯正弦函数。如图2.31（a）所示为振荡电流幅值随δ的变化。当δ为π的偶数倍时，IM最小。当δ为π的奇数倍时，IM最大。

图2.31　电力系统振荡时电流电压的变化

对于系统各元件的阻抗角皆相同、振荡角度δ=180°的特殊情况，系统各点的电压值可用图2.31（b）的图解法求出。因阻抗角都相同，任意两点间的电压降正比于两点间阻抗的大小。在图2.31（b）中，使线段OM、MN和NO′正比于ZM、ZL和ZN。垂直向上，垂直向下，两者相差180°。连接和端点的直线即为系统各点的电压分布线。线段Mm和Nn的长度按电压标尺等于M和N点的电压和Z为δ=180°时系统的振荡中心，其电压等于零。其他各点的电压也可用同样方法求得。

图2.31（c）所示为M、N和Z点电压幅值随δ变化的典型曲线。对于系统各部分阻抗角不同的一般情况，也可用类似的图解法进行分析，此处从略。

（2）电力系统振荡对距离保护的影响

如图2.32所示，设距离保护安装在变电所M的线路上。当系统振荡时，按式（2.49），振荡电流为：

此处，ZΣ代表系统总的纵向正序阻抗。

图2.32　分析系统振荡用的系统接线图

M点的母线电压为：

因此，安装于M点阻抗继电器的测量阻抗为：

在近似计算中，假定h=1，系统和线路的阻抗角相同，则继电器测量阻抗随δ的变化关系为：

将此继电器测量阻抗随δ变化的关系，画在以保护安装地点M为原点的复数阻抗平面上，当全系统所有阻抗角相同时，即可由图2.33证明Zr·M将在ZΣ的垂直平分线OO′上移动。

图2.33　系统振荡时测量阻抗的变化

绘制此轨迹的方法是：先从M点沿MN方向作出相量然后再从其端点作出相量，在不同的δ角度时，此相量可能滞后或超前于相量ZΣ90°，其计算结果见表2.2。将后一相量的端点与M连接即得Zr·M。

表2.2

由此可见，当δ=0°时，Zr·M=∞；当δ=180°时，Zr·M=，即等于保护安装地点到振荡中心之间的阻抗。此分析结果表明，当δ改变时，不仅测量阻抗的数值在变化，而且阻抗角也在变化，其变化的范围为（φK-90°）～（φK+90°）。

在系统振荡时，为了求出不同安装地点距离保护测量阻抗变化的规律，在式（2.61）中，可令ZX代替ZM，并假定m=ZX/ZΣ，m为小于1的变数，则式（2.61）可改写为：

当m为不同数值时，测量阻抗变化的轨迹应是平行于线的一直线簇，如图2.34所示，当m=1/2时，直线簇与+jX轴相交，相当于图2.34所分析的情况，此时，振荡中心位于保护范围的正方向；而当m＜1/2时，直线簇与+jX轴相交，相当于图2.33所分析的情况，此时，振荡中心位于保护范围的正方向；而当m＞1/2时，直线簇则与-jX相交，振荡中心将位于保护范围的反方向。

当两侧系统的电势EM≠EN，即h≠1时，继电器测量阻抗的变化将具有更复杂的形式。按照式（2.60）进行分析的结果表明，此复杂函数的轨迹应是位于直线某一侧的一个圆，如图2.35所示。当h＜1时，为位于上面的圆周1；而当h＞1时，则为下面的圆周2。在这种情况下，当δ=0°时，两侧电势不相等而产生一个环流，故测量阻抗不等于∞，而是一个位于圆周上的有限数值。

图2.34　系统振荡时，不同安装地点距离保护测量阻抗的变化

图2.35　当h≠1时测量阻抗的变化

引用以上推导结果，可以分析系统振荡时距离保护所受到的影响。如仍以变电所M处的距离保护为例，其距离Ⅰ段启动阻抗整定为0.85ZL，在图2.36中以长度MA表示，由此可以绘出各种继电器的动作特性曲线，其中曲线1为方向透镜电器特性，曲线2为方向阻抗继电器特性，曲线3为全阻抗继电器特性。当系统振荡时，测量阻抗的变化如图2.33所示（采用h=1的情况），找出各种动作特性与直线的交点，其所对应的角度为δ′和δ″，则在这两个交点的范围以内继电器的测量阻抗均位于动作特性圆内，因此，继电器就要启动，也就是说，在这段范围内，距离保护受振荡的影响可能误动作。由图中可见，在同样整定值的条件下，全阻抗继电器受振荡的影响最大，而透镜型继电器所受的影响最小。一般而言，继电器的动作特性在阻抗平面上沿方向所占的面积越大，受振荡的影响就越大。

图2.36　系统振荡时M变电所测量阻抗的变化图

此外，根据对图2.33的分析可知，距离保护受振荡的影响还与保护的安装地点有关。保护安装地点越靠近于振荡中心，受到的影响就越大，而振荡中心在保护范围以外或位于保护的反方向时，则在振荡的影响下距离保护不会误动作。

当保护的动作带有较大的延时（例如，延时大于1.5 s）时，如距离Ⅲ段，可利用延时躲开振荡的影响。

（3）振荡闭锁回路

对于在系统振荡时可能误动作的保护装置，应该装设专门的振荡闭锁回路，以防止系统振荡时误动。当系统振荡使两侧电源之间的角度摆到δ=180°时，保护所受到的影响与在系统振荡中心处三相短路时的效果是一样的，因此，就必须要求振荡闭锁回路能够有效地区分系统振荡和发生三相短路这两种不同情况。

电力系统发生振荡和短路时的主要区别如下：

①振荡时，电流和各点电压的幅值均作周期性变化（图2.31），只在δ=180°时才出现最严重的现象；而短路后，短路电流和各点电压的值，当不计其衰减时，是不变的。此外，振荡时电流和各点电压幅值的变化速度较慢，而短路时电流是突然增大，电压也突然降低，变化速度很快。

②振荡时，任一点电流与电压之间的相位关系都随δ的变化而改变；而短路时，电流和电压之间的相位是不变的。

③振荡时，三相完全对称，电力系统中没有负序分量出现；而当短路时，总要长期（在不对称短路过程中）或瞬间（在三相短路开始时）出现负序分量。

④振荡时，测量阻抗的电阻分量变化较大，变化速率取决于振荡周期；而短路时，测时阻抗的电阻分量虽然因弧光放电而略有变化，但分析计算表明其电弧电阻变化率远小于振荡所对应的电阻的变化率。

根据以上区别，振荡闭锁回路从原理上可分为两种：一种是利用负序分量（或增量）的出现与否来实现，另一种是利用电流、电压或测量阻抗变化速度的不同来实现。

构成振荡闭锁回路时应满足以下基本要求：

①系统发生振荡而没有故障时，应可靠地将保护闭锁，且振荡不停息，闭锁不应解除。

②系统发生各种类型的故障（包括转换性故障），保护应不被闭锁而能可靠地动作。

③在振荡的过程中发生故障时，保护应能正确地动作。

④先故障而后又发生振荡时，保护不致无选择性的动作。

现对两种原理的振荡闭锁回路举例简介如下：

1）利用负序（和零序）分量元件启动的振荡闭锁回路

①负序电压过滤器：用以从三相不对称电压中取出其负序分量的回路称为负序电压过滤器。由两个电阻-电容阻抗臂构成的负序电压过滤器的原理接线如图2.37所示。当在其输入端加入三相电压时，应要求在它的输出端只有负序电压输出，为此就必须在考虑过滤器的接线时，使正序和零序电压没有输出。(www.xing528.com)

在三相电压中，零序电压大小相等相位相同，因此，在线电压中没有零序电压分量。在输入端采用线电压，就可以消除零序电压的影响，使它不可能在输出端出现。

正序分量线电压是沿着顺时针的方向依次落后120°。因此，如果能用一个移相电路，例如，使向超前方向移动30°，再使向滞后方向移动30°，然后将两者相加，则输出电压就等于零，也就是用此方法能消除正序电压的影响。

图2.37　负序电压过滤器原理接线图

基于上述原则，在图2.37的接线中，如果选择两臂参数的关系为：

则当输入端有正序电压加入时，其相量图如图2.38（a）所示，在m—n端的输出电压为：

当输入端有负序电压加入时，其相量图如图2.38（b）所示，由于负序线电压的相位关系和正序电压相反，因此，在m—n端的空载输出电压为：

此结果表明，过滤器的空载输出电压与输入端的负序相电压成正比，且相位较超前30°。

图2.38　负序电压过滤器相量图

当过滤器输入端加入三相正序电压时，实际上在输出端也会有一个不平衡电压的输出，产生的原因是各元件的实际阻抗值与计算值有所偏差，因而不能完全消掉正序电压的影响。例如，由于各元件的参数制作不准确，阻抗随着环境温度的变化而改变，阻抗随着外加电压的变化而改变，以及阻抗随着系统频率的变化而改变等，都会使过滤器出现不平衡电压。此外，当系统中出现五次谐波分量的电压时，由于它的相位关系和负序分量相似，因此，也会在输出端有电压输出，可能引起保护装置的误动作。必要时可在输出端加装五次谐波滤波器以消除其影响。顺便指出，根据对称分量的基本原理，只要将引入负序电压过滤器的三相端子中的任意两个调换一下（例如将A接B、B接A），即可得到正序电压过滤器。

②负序电流过滤器：用以从三相对称电流中取出其负序分量的回路称为负序电流过滤器。构成负序电流过滤器时，应设法消除正序和零序电流的影响，只输出与负序电流成正比的电压。目前常用的一种负序电流过滤器的原理接线如图2.39所示，主要由电抗互感器TX和中间变流器LB组成。

图2.39　负序电流过滤器原理接线图

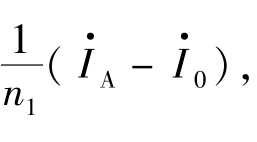TX的原边有两个匝数相同的绕组，分别加入电流和，副边的开路电压与所加电流成正比，且相位超前电流90°，可用表示。LB的原边也有两个绕组，其中W1加入电流另一个1/3W1中加入电流（）。设LB的变比为n1，则其副边电流为在R上的压降即为根据图2.39的接线，在m—n端子上的输出电压可表示为：

当输入端加入正序电流时，其相量图如图2.40（a）所示，输出电压为：

如果选取参数为，则，也就是可以消除正序电流的影响。

图2.40　负序电流过滤器的相量图

当只有零序电流输入时，因，因此，在TX和LB原边的安匝互相抵消，即

如果只输入负序电流时，如图2.40（b）所示，输出电压为：

即输出电压与成正比而且同相位，从而达到滤出负序电流的目的。

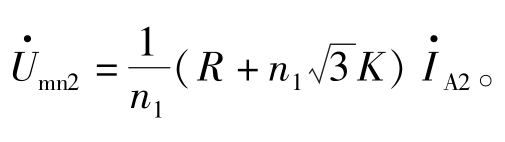顺便指出，如果在参数选择时，使，则当只有正序分量时，输出电压为Umn1=，只有负序分量时，输出电压为当同时存在有正序和负序分量时，则输出电压为：

就是一个的复合电流过滤器，式中，K1、K2为比例常数。

③集成电路型对称分量过滤器：上述对称分量过滤器的原理可用各种不同的电子器件实现，目前广泛应用集成电路构成。

④利用负序（或零序）电流增量元件启动的振荡闭锁回路：可以利用短路时出现的负序或零序电流分量启动振荡闭锁回路，也可以利用这些分量的增量或突变量来完成这一任务。

产生负序（零序）电流增量的原理接线如图2.41所示。由中间变流器LBA、电阻R1、R2和电抗互感器TXBC组成了一个负序电流过滤器，其输出电压经调节定值电阻R4、R5后，接入全波整流器1BZ，整流后的输出电压经微分电容C1接入启动元件QDr的一组线圈。反映零序电流增量的回路由中间变流器LB0及电阻R3组成，当有零序电流出现时，在R3上即可获得一个与3I0成正比的输出电压，此电压经调节定值电阻R6、R7和2BZ整流后与1BZ并联，也接于C1和QDr上。R8和R9作为整流回路的负载，并为电容器C1提供放电回路。L和C2用以滤去整流后的二次谐波。

图2.41　产生负序和零序电流增量原理图

在上述接线中，当I2或3I0突然增加时，1BZ或2BZ两端的输出电压也突然增大，此时，电压经QDr的线圈对C1充电，QDr即反应于这个充电电流而动作，当C1充满电以后，QDr中的电流即行消失，而QDr可利用另一个自保持线圈而保持在动作状态。如果I2或3I0是平缓增大，则整流后的输出电压也随之成正比地缓慢增大，此时，经C1的充电电流很小，QDr不能动作。对于数值平稳的I2或3I0，其整流后的输出电压不变，因而不能通过C1而产生电流，故这个回路只能反应于I2或3I0的数量突增而使QDr动作。

在系统发生振荡而无短路时，没有负序和零序电流增量，图2.41中的QDr继电器不动作。而由于振荡时电流增大，电压减小，使一过流继电器或距离Ⅲ段的阻抗继电器动作，立即启动振荡闭锁执行继电器，断开距离保护Ⅰ段和Ⅱ段的跳闸回路，将保护闭锁。但是，当发生短路时，产生的负序电流增量使QDr短时动作，使振荡闭锁执行继电器的动作延缓0.2～0.3 s。在此时间内，距离保护的Ⅰ段和Ⅱ段可以动作于跳闸。如距离Ⅱ段动作范围外短路，其Ⅰ、Ⅱ段均不动作，则在0.2～0.3 s后，振荡闭锁执行继电器动作，将距离Ⅰ、Ⅱ段闭锁。距离Ⅲ段的延时一般大于振荡周期，不会受振荡的影响而误动，故不需要闭锁。

2）反映测量阻抗变化速度的振荡闭锁回路

在三段式距离保护中，当其Ⅰ、Ⅱ段采用方向阻抗继电器，其Ⅲ段采用偏移特性阻抗继电器时，如图2.42所示，根据其定值的配合，必然存在着ZⅠ＜ZⅡ＜ZⅢ的关系。可利用振荡时各段动作时间不同的特点构成振荡闭锁。

图2.42　三段式距离保护的动作特性

当系统发生振荡且振荡中心位于保护范围以内时，由于测量阻抗逐渐减小，因此，ZⅢ先启动，ZⅡ再启动，最后ZⅠ启动。而当保护范围内部故障时，由于测量阻抗突减小，因此，ZⅠ、ZⅡ、ZⅢ将同时启动。基于上述区别，实现这种振荡闭锁回路的基本原则是：当ZⅠ～ZⅢ同时启动时，允许ZⅠ、ZⅡ动作于跳闸，而当ZⅢ先启动，经t0延时后，ZⅡ、ZⅠ才启动时，则把ZⅠ和ZⅡ闭锁，不允许它们动作于跳闸。按这种原则构成振荡闭锁回路的结构框图如图2.43所示。

图2.43　反映测量阻抗变化速度的振荡闭锁回路结构框图

※（4）新型振荡闭锁工作原理

1）启动元件动作160 ms以内开放保护的条件

当距离保护的启动元件是一种反映正负序综合电流工频变化量的过电流元件，在单纯系统振荡而无故障时，启动元件初期不动作，其后因电流互感器的饱和而可能动作；所以按躲过最大负荷电流整定的正序过电流元件先于启动元件动作，否门闭锁了“保护开放”的逻辑；在线路故障同时伴有振荡时，启动元件和正序过电流元件同时动作，但由于正序过电流元件经延时10 ms输出，启动元件先于正序过电流元件动作，结果否门闭锁解除，由启动元件开放保护160 ms，即开放条件是：启动元件动作瞬间，若按躲过最大负荷整定的正序过电流元件不动作或动作时间不足10 ms，则将保护开放160 ms，其原理逻辑框图如图2.44所示。

图2.44　振荡闭锁原理逻辑框图

2）系统振荡中不对称故障时开放条件

在系统振荡中发生不对称短路故障时，振荡闭锁分量元件开放保护的动作条件为：

根据振荡对称的特征，所以正序电流幅值很大，而零序和负序电流较小，式（2.68）不满足要求，将保护闭锁。

系统振荡时又发生区内不对称短路，将有较大的负序电流分量或零序电流分量，此时，式（2.68）是否成立，取决于短路时刻两侧系统电势角摆开程度。如果系统电势角不够大，振荡电流数值较小，而不对称短路时序分量电流的数值很大，则式（2.68）成立；保护装置立即开放，短路时刻若系统两侧电势角已摆开较大，此时系统电压低，正序分量电流足够大，使式（2.68）暂时不成立；保护装置暂时被闭锁，但系统电势角还会变化，则装置将在系统电势角逐步减小时开放，在不利的情况下，可能由一侧瞬时开放保护跳闸后，另一侧相继跳闸。

系统振荡中，若又发生区外不对称故障，这时，相间、接地距离元件都将可能误动，但是，可以通过正确地设置制动系数m，使式（2.68）在此情况下可靠不成立，以确保振荡闭锁序分量元件不开放保护。装置中的m值就是根据最不利情况下以振荡闭锁序分量元件不开放保护为原则，并有一定裕度。

3）系统振荡中发生对称性故障时保护开放的条件

①振荡中心电压在启动元件开放160 ms以后或系统振荡过程中，如果又发生了三相短路故障，则上述两个开放保护的条件均不成立，不能开放保护。因此，还必须设置专门的振荡判别条件。

系统振荡时，振荡中心的电压可以由保护装置算得：

式中　U1——母线正序电压；

φ1——正序电压、电流夹角。

系统振荡时，振荡周期在180°左右，振荡中心电压Uos在0.05UN左右，三相短路故障电阻就是弧光电阻，该电阻上压降的幅值也在0.05UN左右。

②振荡中心电压与三相短路弧光电阻上的压降IRg的关系。若系统阻抗角为90°，振荡电流Iswi垂直于相量，并与振荡中心电压同相位。

假设线路为感抗，在系统中发生三相短路故障时，短路电流也与垂直，而且三相短路时，过渡电阻凡即弧光电阻上的压降与同相位，并等于如图2.45（a）所示，母线正序电压由此可见，三相短路弧光电阻上的压降虽然不能测到，但可以由振荡中心电压代替，说明反映了弧光电阻上的压降。但是，系统实际阻抗角不等于90°，振荡中心电压仍然可以反映弧光电阻压降，这可由图2.45（b）得到证明。通过d点做补偿角θ=90°-φL。相量为线路电感分量上的电压，为线路电阻分量上的电压，则线路上的电压降因为三相短路时母线上的电压等于线路压降与弧光电阻压降之和，因此，电压相量就是三相短路时弧光θ电阻压降。由于超高压线路θ角很小，所以，oa=oc=Uos=UM1cos（φ1+θ），则oa≈UM1cosφ1，这说明振荡中心电压仍可以反映弧光电阻压降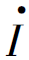Rg。

图2.45　系统振荡中心电压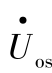相量图

③系统振荡中发生对称性短路故障的判据。三相短路时弧光电阻上的压降约5%UN，而系统振荡时振荡中心电压Uos，在振荡周期的180°左右一段时间内降到最低点也约为5%UN。所以，振荡中心电压在式（2.69）表示的范围内以三相短路弧光电阻压降相近，很难区分振荡还是三相短路。

实际上，振荡中心电压在（0.03～0.08）UN范围内，是指两侧系统E，势角摆开范围为171°～183.5°，如果按最大振荡周期3 s计算从171°～183.5°需要104 ms，其后振荡中心电压值就偏离式（2.69）的范围。所以，在满足判据式（2.69）后，经过150 ms延时可以有效地区分三相短路与振荡。延时后式（2.69）仍能成立，判为三相短路，立即开放保护，否则就是系统振荡，闭锁保护。

④振荡中三相短路后备保护动作判据。为了保证三相短路故障时，保护可靠不被闭锁，装置可设置如下后备动作判据，并延时500 ms后开放保护。

该段振荡中心电压范围对应系统电势角为151°～191.5°，按最大振荡周期3 s计算，振荡中心在该区域停留时间为373 ms，所以，装置对应的延时取500 ms已有足够裕度。