电力拖动系统负载转矩特性优化

电力拖动系统是由电动机拖动，并通过一些传动机构带动生产机械运转的机电运动的动力学整体。虽然电动机的种类繁多，其特性又不一样，而生产机械的性质也是多种多样的，但若从动力学的角度来讲，则都应遵循动力学的统一规律，因此，下面先分析电力拖动系统的运动方程式，进而分析电力拖动系统的稳定运行条件。

1.电力拖动系统的运动方程式

图3.15所示为一单轴电力拖动系统简图，它是由电动机M 产生转矩T，并由T 来克服负载转矩TL，以驱动生产机械运动的系统。当这两个转矩平衡时，传动系统保持恒速转动，转速n不变，加速度dn/dt等于零，即T=TL 时，n=常数，dn/dt=0，这种运动状态称为静态（相对静止状态）或稳态（稳定运转状态）。

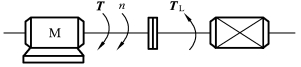
图3.15　单轴电力拖动系统简图

当T≠TL 时，电动机会加速或减速，转速n就要发生变化，转速的变化大小与传动系统的转动惯量J 有关，即满足

式中：T 为电动机产生的转矩；TL为单轴电力拖动系统的负载转矩；J 为单轴电力拖动系统的转动惯量；n为单轴电力拖动系统的转速。

式（3.29）就是单轴电力拖动系统的运动方程式。由式（3.29）可得如下结论。

（1）当T=TL 时，dn/dt=0，n=常数，系统恒速运转，系统处于稳态。稳态时，电动机产生转矩的大小，仅由电动机所带负载（生产机械）决定。

（2）当T＞TL 时，dn/dt＞0，传动系统作加速运动。

（3）当T＜TL 时，dn/dt＜0，传动系统作减速运动。

系统处于加速或减速的运动状态称为动态。

电动机的转矩平衡方程式为

式中：T2 为动态转矩或为电动机轴上的输出转矩。

2.电力拖动系统中的拖动转矩和制动转矩

1）转矩正方向的规定

由于电力拖动系统有各种运动状态，对应的运动方程式中的转速和转矩就有不同的符号。生产机械和电动机是以同一转速旋转的，所以一般用转动方向作为参考来确定转矩的正、负。

如图3.16所示，若设电动机转速沿逆时针旋转为正，则约定电动机转矩T 与n 方向一致为正向，负载转矩TL 与转速n方向相反为正向。

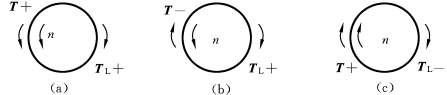
图3.16　电力拖动系统转矩方向的规定

2）拖动转矩与制动转矩

按上述约定的判定规则，就可以从转矩和转速的符号判定T 与TL 的性质。

（1）若T 与n 符号相同（同为正或同为负），则表示T 的作用方向与n 相同，T 为拖动转矩；若T 与n 符号相反，则表示T 的作用方向与n 相反，T 为制动转矩。

（2）若TL 与n符号相同（同为正或同为负），则表示TL 的作用方向与n相反，TL 为制动转矩；若TL 与n符号相反，则表示TL 的作用方向与n 相同，TL 为拖动转矩。T 和TL 的符号判定如图3.17所示。

3.生产机械的机械特性

同一转轴上负载转矩和转速之间的函数关系称为生产机械的机械特性，即n=f（TL）。由于不同生产机械在运动中所受阻力的性质不同，其机械特性曲线的形状也不尽相同，一般可归纳为以下三种典型的机械特性。

1）恒转矩型负载的机械特性

所谓恒转矩型负载是指负载转矩TL 的大小不随转速n变化而变化的负载，属于此类的生产机械有各种提升设备、皮带传输机构以及金属切削机床等。

根据负载转矩TL 与生产机械运动方向之间的关系，恒转矩型负载可分为反抗性恒转矩负载和位能性恒转矩负载两种。

反抗性恒转矩也称为摩擦转矩，是因摩擦和非弹性体的压缩、拉伸与扭转等作用产生的负载转矩，机床切削过程中的切削力所产生的负载就是反抗性恒转矩负载。反抗性恒转矩负载的方向恒与运动方向相反，若运动方向发生改变时，负载转矩的方向也会发生改变，因此它总是阻碍运动的，其特性曲线在第一象限或第三象限，具体方向判定如图3.17所示。

位能性恒转矩负载是由于物体的重力和弹性体的压缩、拉伸与扭转等作用产生的负载转矩。如卷扬机起吊重物时重力所产生的负载转矩就是位能性恒转矩负载。位能性恒转矩负载的作用方向恒定，与运动方向无关，它有时阻碍运动，有时又促进运动（如重物的提升及下降），其特性曲线在第一象限或第四象限，具体方向判定如图3.18所示。

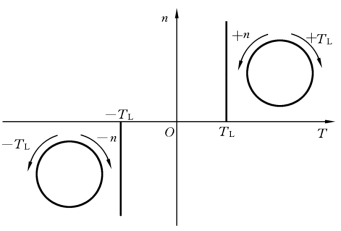
图3.17　反抗性恒转矩负载的机械特性曲线(www.xing528.com)

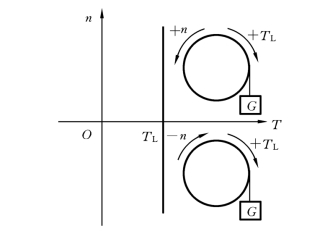
图3.18　位能性恒转矩负载的机械特性曲线

反抗性恒转矩负载TL 与位能性恒转矩负载TL 比较：反抗性恒转矩负载TL 的符号总是正的；位能性恒转矩负载TL 的符号则有时为正，有时为负。

2）恒功率型负载的机械特性

恒功率型负载的转矩与转速n成反比，即PL=TLn/9550，如图3.19所示。例如，车床加工：在粗加工时，切削量大，负载阻力大，要低速运行；在精加工时，切削量小，负载阻力小，要高速运行。无论选择什么样的加工方式，不同转速下，切削功率基本不变。

3）离心式通风机型负载的机械特性

离心式通风机型负载是按离心力原理工作的，如离心式鼓风机、水泵等。它们的负载转矩TL 与n的平方成正比，即TL=Cn2，C 为常数，如图3.20所示。

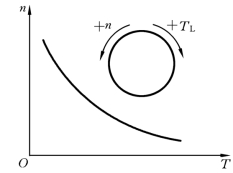
图3.19　恒功率型负载的机械特性曲线

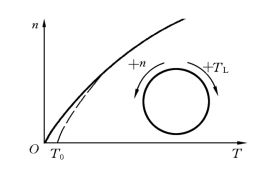
图3.20　离心式通风机型负载的机械特性曲线

应当指出的是，实际负载可能是单一类型的，也可能是几种典型类型的综合。比如实际通风机除了主要的通风机性质的负载特性外，轴上还有一定的摩擦转矩T0，所以，实际通风机的机械特性应是TL=T0+Cn2，如图3.20所示的虚线。

4.电力拖动系统的稳定运行条件

1）概述

在电力拖动系统中，电动机和生产机械是连成一体的，要使系统运行合理，就要想办法使电动机的机械特性和负载的机械特性尽量相配合。特性配合好的基本要求是系统能稳定运行。

电力拖动系统的稳定运行包含两重含义：一是系统应能以一定的速度匀速运转；二是系统受到某种外部干扰而使运行速度稍有变化时，应保证在干扰消除后系统能恢复到原来的运行速度。

2）稳定工作点的判别

稳定工作点的判别包括系统平衡点的判别（图3.21（a））和系统稳定平衡点的判别（图3.21（b）），图中曲线1是电动机的机械特性曲线，曲线2是负载的机械特性曲线。

（1）稳定运行的必要条件。

稳定运行的必要条件也就是系统平衡点的判别。若要保证电动机恒速运转，必要条件是电动机轴上的拖动转矩T 与电动机轴上的负载转矩TL 应大小相等、方向相反，能相互平衡。从图3.21（a）可以得出结论：在OT-n 坐标系中，n=f（TL）与n=f（T）必须有交点，即T=TL。如图3.21（a）所示的a、b两点就称为系统的平衡点。

（2）稳定运行的充分条件。

稳定运行的充分条件也就是系统稳定平衡点的判别。机械特性曲线存在交点只是保证系统稳定的必要条件，并非充分条件，实际上只有a 点是稳定的平衡点，b 点不是稳定的平衡点（图3.21（b）），其原因如下。

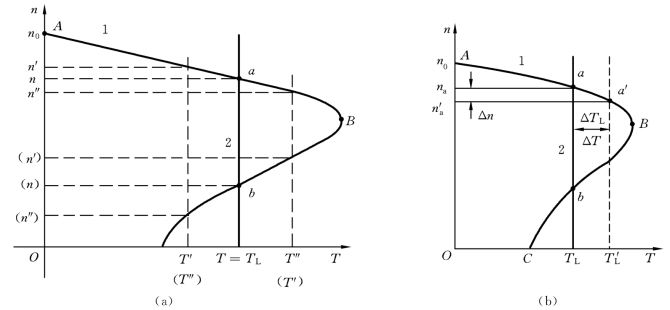
图3.21　系统稳定平衡点的判别

①a点是稳定的平衡点。原因是当系统出现干扰，比如TL=TL+ΔTL（ΔTL 为扰动）时，电动机来不及反应，仍工作在a点，其电磁转矩仍为T，此时有

②b点不是稳定的平衡点。当系统出现干扰，比如TL=TL+ΔTL（ΔTL 为扰动）时，有

对于恒转矩型负载，电动机转速变化（n增加或减小）时，机械特性曲线应具有向下倾斜的特点，这样系统才能稳定运行。若特性曲线上翘，则系统不能稳定运行。

由以上分析可以总结出机电传动控制系统稳定的必要充分条件如下。

（1）电动机的机械特性曲线n=f（T）和负载的机械特性曲线n=f（TL）有交点（即拖动系统的平衡点）。

（2）当干扰使转速大于平衡点所对应的转速时，必须有T′＜TL；当干扰使转速小于平衡点所对应的转速时，必须有T′＞TL。只有同时满足上述两个条件的平衡点，才是拖动系统的稳定平衡点，即只有这样的特性配合，系统在受到外界干扰后，才具有恢复到原来平衡状态的能力并进入稳定运行。

图3.22所示为异步电动机拖动直流他励发电机工作情况的特性曲线，根据系统稳定的判别条件，B 点符合稳定运行条件，所以B 点是稳定的平衡点。（注意：此时负载的机械特性硬度大于电动机的机械特性硬度。）

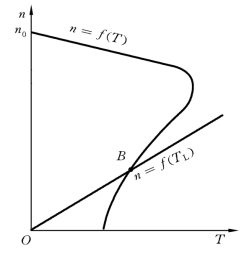
图3.22　异步电动机拖动直流他励发电机工作时的特性曲线