齿面接触疲劳强度的计算方法

齿面接触疲劳强度计算的目的是防止发生齿面点蚀，其计算依据是2.4节中介绍的赫兹公式［式（2-28）］和接触疲劳强度条件［式（2-29）］。当将其用于直齿圆柱齿轮的啮合情况时，有轮齿的齿面接触疲劳强度条件为

式中　Fnca——作用于轮齿上的法向计算载荷；

L——轮齿接触线长度；

E1、E2——两个齿轮材料的弹性模量；

μ1、μ2——两个齿轮材料的泊松比；

ρ1、ρ2——啮合点处两个齿廓的曲率半径，其中“+”用于外啮合，“-”用于内啮合；

［σH］——齿面接触疲劳强度计算的许用接触应力。

由式（5-8）可知，在齿轮材料、轮齿的受力和轮齿接触线长度确定后，齿面接触疲劳强度主要与啮合点处两个齿廓的曲率半径有关。

令式（5-8）中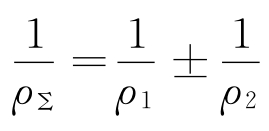，ρΣ称为综合曲率半径，1/ρΣ为综合曲率。在齿轮工作过程中，齿廓啮合点的位置是变化的，渐开线齿廓上各点的曲率半径也各不相同，因此各啮合点的综合曲率半径一般也不相等。图5-15给出了渐开线齿轮沿啮合线各点的综合曲率1/ρΣ的变化情况和接触应力σH的变化情况。

对于端面重合度εα≤2的直齿圆柱齿轮传动，在双齿对啮合区（图5-15中的B2C段、B1D段），载荷由两对齿承担，并且啮合点的综合曲率1/ρΣ较大，故接触应力小于单齿对啮合区。在单齿对啮合区（图5-15中的CD段），全部载荷由一对齿承担，因而轮齿的载荷最大，此外啮合点的综合曲率1/ρΣ较小，所以有较大的接触应力。虽然在单齿对啮合区中节点P处的接触应力不是最大值，但考虑到节点P处的综合曲率半径ρΣ确定较方便，并且实际工作中点蚀往往首先出现在靠近节线的齿根面上，所以通常取节点P作为齿面接触强度的计算点。

图5-15　齿面的接触应力

对于标准齿轮传动，在节点P处的法向计算载荷为

在节点P处的两轮齿廓的曲率半径为

所以节点P处的综合曲率为

令上式中d2/d1=z2/z1=u，称u为齿数比，则节点P处的综合曲率为(www.xing528.com)

将节点P处的法向计算载荷、综合曲率代入式（5-8），并引入Zε以考虑重合度带来的影响，经整理后得

令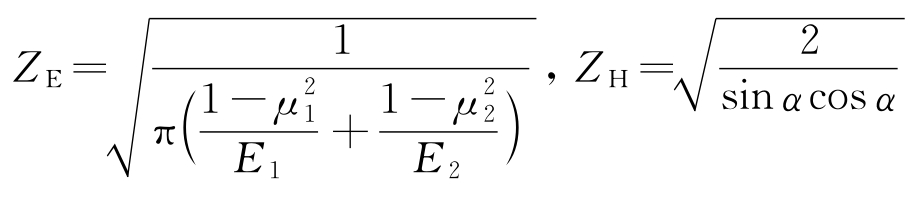，则得到直齿圆柱齿轮传动的齿面接触疲劳强度条件为

式中　ZE——材料弹性系数，对于常用齿轮材料的组合，其值可查表5-6；

ZH——节点区域系数，用来考虑节点处齿廓形状对接触应力的影响，对于标准齿轮传动（α=20°），ZH=2.5；

Zε——接触强度的重合度系数，可根据齿轮传动的重合度εα，查图5-16确定，εα由附表1-2公式计算或由齿数z1、z2查图5-17来确定；

b——齿轮的啮合宽度，常取为大齿轮的宽度（mm）。

表5-6　材料弹性系数ZE　单位：

设齿宽系数φd=b/d1，将b=φdd1代入式（5-9），可得齿面接触疲劳强度的设计公式为

在齿面接触疲劳强度计算中，配对齿轮的接触应力是相等的。但两个齿轮的材料、热处理方法、齿面硬度及应力循环次数不同，因而许用接触应力［σH1］和［σH2］一般不相等。因此，在使用设计公式（5-10）或校核公式（5-9）时，应取［σH1］和［σH2］两者中的较小者代入计算，即取［σH］=min｛［σH1］，［σH2］｝代入计算。

在采用设计公式（5-10）初步计算小齿轮的分度圆直径d1时，由于齿轮的几何尺寸未确定，因此载荷系数中的动载系数Kv、齿间载荷分配系数KHα及齿向载荷分布系数KHβ不能预先确定。此时可试选一个载荷系数Kt（一般取Kt=1.2～1.6），计算后得到一个初算后的分度圆直径d1t，再按d1t确定有关的几何尺寸，从而确定动载系数Kv、齿间载荷分配系数KHα及齿向载荷分布系数KHβ，计算载荷系数K。若K与试选的Kt相差不大，则不需要修改原来的计算结果；若K与Kt相差较大，则应按式（5-11）对试算得到的分度圆直径d1t进行修正：

图5-16　接触强度的重合度系数

图5-17　外啮合标准齿轮传动的端面重合度系数

注：使用时按z1和β查出εα1，按z2和β查出εα2，εα=εα1+εα2

由式（5-10）可知，在齿轮的齿宽系数、材料及传动比已选定的情况下，影响齿轮齿面接触疲劳强度的主要因素是小齿轮的分度圆直径。小齿轮分度圆直径越大，齿面的接触应力越小，齿轮的齿面接触疲劳强度越高。